Математика/Математическое моделирование

Аспирант ПензГТУ Мокроусов Д.А., студент ПГУ Демин Е.С.,
к.т.н. Карпухин Э.В., д.т.н. Демин С.Б.

Пензенский государственный технологический университет (ПензГТУ)
Пензенский государственный университет (ПГУ)

К вопросу повышения точности моделирования магнитных полей магнитострикционных уровнемеров накладного типа со сложной геометрией акустического тракта

Аннотация: В статье приводится способ повышения точности численного моделирования магнитных полей магнитострикционных преобразователей уровня накладного типа для байпасных систем со сложной геометрией акустического тракта путем использования модификации метода Ричардсона. Также демонстрируется эффективность предложенной методики

Ключевые слова: магнитострикционные преобразователи уровня накладного типа, эффективные численные методы

В настоящее время в различных отраслях промышленности широкое применение нашли магнитострикционные уровнемеры (МПУ) накладного типа [1,3,4]. Главными достоинствами этих приборов является высокая точность и разрешающая способность при относительной простоте конструкции и низкой себестоимости изготовления. Одной из разновидностей таких приборов являются МПУ накладного типа для байпасных систем со сложной геометрией акустического тракта [1]. Являясь сравнительно новым классом подобных устройств, они требуют проведения дополнительных исследований с целью улучшения их характеристик и внедрения в технологические процессы различных промышленных предприятий.

Из-за сложности проведения натурного эксперимента измерения слабых магнитных полей, решение подобной задачи предлагается осуществлять методами математического моделирования с применением ЭВМ. Ключевым моментом здесь является численный расчет характеристик магнитного поля, на основании которого определяются выходные параметры МПУ накладного типа. В настоящее время известны различные методики проведения такого расчета, которые обладают своими преимуществами и недостатками [2,3]. Результаты подобных исследований уже позволили провести вычислительные эксперименты магнитных полей МПУ накладного типа и создать устройства с улучшенными параметрами [1,3,4].

Однако существующие численные методы, реализованные в виде комплексов программ, решения разностных уравнений магнитных полей МПУ, оказываются малоэффективными при проведении расчетов в областях со сложной геометрией акустического тракта и требуют дополнительной доработки. Наиболее целесообразно здесь применение метода Ричардсона, попеременно-треугольного метода, различных итерационных методов вариационного типа. Причем все они, кроме первого, требуют предварительного расчета многих параметров, позволяя при этом решать задачу в областях с ярко выраженной неоднородностью сред.

В рамках решаемой задачи, расчетная область МПУ накладного типа для байпасных систем не обладает значительной неоднородностью, поэтому в данном случае эффективным будет использование метода Ричардсона. Основные преимущества и суть данного метода заключаются в следующем.

Подход к построению итерационной схемы Ричардсона заключается в изучении поведения ошибки . Такой анализ позволяет выбрать параметр , рассматривая характер изменения ошибки при переходе от n-ой к (n+1)-ой итерации, причем

, (1)

где – массив точных значений потенциалов, – массив потенциалов, полученный в результате -ой итерации.

Действительно, на границах расчетной области заданы краевые условия и ошибка на них равна нулю. Поэтому внутри области функцию можно разложить в ряд Фурье, который будет иметь вид

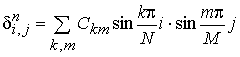, (2)

где коэффициенты разложения зависят от параметра и номера n итерации [2,5]. Чем меньшее значение имеет коэффициент , тем меньшее влияние гармоника k,m оказывает на общую ошибку .

Поэтому выбор оптимального значения следует осуществлять из критерия наилучшего подавления гармоник ошибки в средней части спектра. Учтем также, что гармонический состав ошибки от итерации к итерации может изменяться, и для максимальной эффективности метода следует выбирать новое значение на каждом шаге [2].

В использовании набора оптимальных значений заключается основное преимущество метода Ричардсона. Медленная сходимость других методов (метода простой итерации, Зейделя, верхней релаксации [2,3,5]) объясняется тем, что низко- и высокочастотные гармоники ошибки подавляются с одинаковой скоростью и общая сходимость метода определяется лишь крайними границами спектра ошибки. Введение же набора оптимальных значений обеспечивает поочередное подавление всех гармоник ошибки и её равномерное быстрое уменьшение за небольшое число итераций.

Рассмотрим способы получения набора оптимальных значений .

Для этого, полагая зависящим от номера итерации, запишем итерационную схему в виде:

. (3)

В силу того, что соотношение аналогичное (3) будет выполняться и для массива точных значений потенциалов и с учетом (1), для ошибки можно записать:

. (4)

Тогда, обозначив начальную ошибку (при n=0) через , получим выражение для ошибки после итераций:

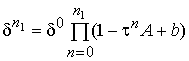. (5)

Используя (5), можно показать, что для наилучшего подавления ошибки за итераций, параметры должны выбираться исходя из условия [2]:

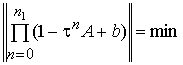. (6)

На практике, отыскание набора параметров , минимизирующих норму (6), обычно заменяют отысканием , где и – наибольшее и наименьшее собственные числа матрицы коэффициентов системы A, при которых многочлены Чебышева первого рода степени , принимают наиболее близкие к нулю значения. Тогда, как известно [2]:

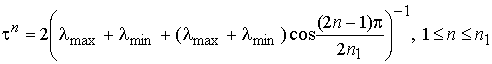. (7)

Рассчитанные в соответствии с (7), первые элементы последовательности имеют порядок и потому на первых итерациях наиболее активно подавляются гармоники ошибки соответствующие правой части спектра. Составляющие же левой части спектра гармоники подавляются на этих итерациях медленно. Однако они активно подавляются старшими элементами последовательности , имеющими порядок , т.е. при . Таким образом, происходит значительное равномерное уменьшение ошибки за итераций [2,5].

При решении практических задач на ЭВМ методом Ричардсона, обычно задаются сравнительно небольшим числом , рассчитывают параметры по формуле (7) и повторяют серии по итераций (3) с одними и теми же параметрами до тех пор, пока не выполнится некоторый критерий точности.

Основной трудностью при использовании метода Ричардсона является частичная проблема отыскания собственных чисел и массива , который, как известно [2,3,4], для систем разностных уравнений магнитных полей МПУ накладного типа обладает большим размером и является плохо обусловленным. Для этого могут применяться различные приближенные методики [5].

Метод Ричардсона характеризуется высокой скоростью сходимости. Известно, что при использовании оптимального набора параметров число итераций на сетке размером узлов зависит от заданной точности следующим образом [2]:

. (8)

График выражения (8) при показан на рисунке 1.

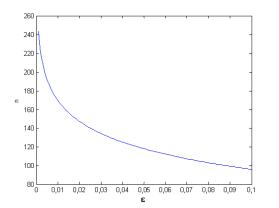
Рисунок 1 – Зависимость числа итераций от требуемой точности по методу Ричардсона

На рисунке 1 видно, что для достижения точности потребуется по методу Ричардсона потребуется выполнить , что при современных вычислительных ресурсах ЭВМ является вполне приемлемым.

Таким образом, решение системы конечно-разностных уравнений вида магнитного поля МПУ накладного типа для байпасных систем наиболее эффективно искать с использованием метода Ричардсона. Последовательность оптимальных значений параметров для него предлагается определять на основе равенства (7) и с их помощью рассчитать неизвестные потенциалы по итерационной формуле (3).

Литература:

1. Демин С.Б. Магнитострикционные системы для автоматизации технологического оборудования: Монография. – Пенза: ИИЦ ПГУ, 2002. – 182 с.

2. Демирчян К.С., Чечурин В.Л. Машинные расчеты электромагнитных полей. – М.: Высшая школа, 1986. – 240 с.

3. Карпухин Э.В., Демин Е.С, Демин С.Б. К вопросу применения эффективных численных методов для моделирования магнитострикционных приборов уровня. Вестник Тамбовского государственного технического университета. – 2012. – Т.18. – №11. – С.58-64.

4. Мокроусов Д.А., Карпухин Э.В., Демин С.Б., Дятков В.С. Применение численных методов для расчета магнитных полей в магнитострикционных уровнемерах. Вестник Ижевского государственного технологического университета. – 2013. – №3. – С. 102-104.

4. Самарский А.А., Гулин А.В. Численные методы. – М: Наука, 1989. – 432 с.