Masich I.S.

Siberian State Aerospace University, Russia

Comparative efficiency of two schemes of local search

in the optimization of pseudo-Boolean functions

Two schemes of local search are considered in the paper - steepest descent and local descent with the transition to the first improvement. About the effectiveness of the steepest descent algorithm earlier in [1] the following results were obtained (Theorems 1 and 2).

Theorem 1. Identifying the maximum point of the unimodal monotone on function f by the algorithm "steepest descent" from the starting point , , requires the calculation of the values of f at points of :

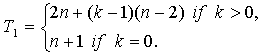
Consequence 1.

.

Theorem 2. Identifying the maximum point of the unimodal monotone on function f by the algorithm "steepest descent" requires on the average the calculation of values of f at points of :

.

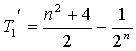We obtain similar estimates for the local search algorithm with the transition to the first improvement.

Theorem 3. Identifying the maximum point of the unimodal monotone on function f by the algorithm "local search with the transition to the first improvement" from the starting point , , requires on the average the calculation of values of f at points of :

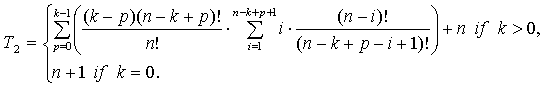
Proof. If then evaluation of complexity follows directly from the definition of an unimodal function [2]. Let . The probability that the first selected point belongs to equal , and the probability that belongs to equal . Thus, the algorithm after viewing one point moves at this point with probability . Correspondingly, the algorithm will make the transition to the next point after viewing i points with probability

.

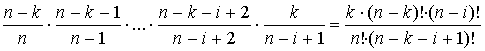Algorithm will find a solution with the best value of the function on the average after

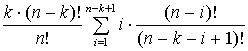
calculations. In further stages, evaluation of complexity is calculated similarly. At the point the algorithm will make n calculations else. Incrementally adding evaluation of complexity we obtain . ■

Consequence 2.

.

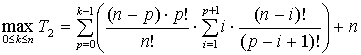Proof. Obviously. ■

Theorem 4. Determination of the maximum point of the unimodal monotone on function f by the algorithm "local search with the transition to the first improvement" requires on the average the calculation of values of f at points of :

.

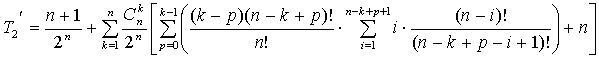Proof. The point is chosen arbitrarily, thus: : . Hence we have

.

Thus, the mathematical expectation for the required calculations of f to determine equal to . ■

It follows from theorems 1-4 and consequences 1-2 that the local search with the transition to first improve is the less time consuming algorithm than the steepest descent. Moreover, as can be seen from the graph in figure 1, its advantage growths when dimension increases. Figure 1 shows the graph of dependence the value of complexity evaluation of the algorithms on the average from the dimension of the problem (value n); solid line - steepest descent, dotted - local search with the transition to the first improvement.

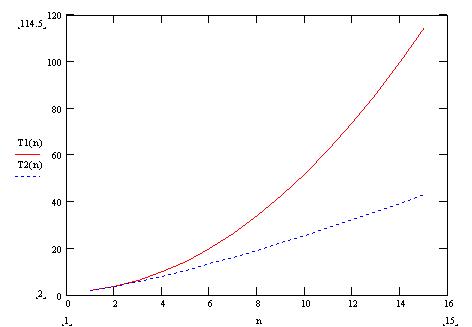
Figure 1 - Comparison of complexity of the algorithms

References

1. Antamoshkin A.N. Regular optimization of pseudo-Boolean functions. – Krasnoyarsk University publishing house, 1989.

2. Masich I.S. Heuristic algorithms for searching boundary points in pseudo-Boolean optimization problems. Materiály IX mezinárodní vědecko - praktická konference «Efektivní nástroje moderních věd – 2013». - Díl 40. Matematika: Praha. Publishing House «Education and Science», p. 54-57.