Физика/2 Физика твердого тела

Д.ф.-м.н. Каримов А.В., к.т.н. Рахматов А.З*.,

Абдулхаев О.А., Каримов А.А.

Физико-технический институт НПО «Физика–Солнца» АН Республики Узбекистан. 100084, г. Ташкент, ул. Бодомзор йули, 2б; e-mail: karimov@uzsci.net. *ОАО “Foton”; e-mail: plan-foton@mail.ru

Влияние гамма и электронного облучения

на прямое падение напряжения мощного

высокочастотного диода

В настоящее время широкое распространение получают силовые диоды, используемые в различных областях электронной техники. Для оптимизации их параметров начинает входить в практику радиационное воздействие. При этом наряду с улучшением быстродействия возможны статические потери мощности за счет увеличения прямого падающего напряжения.

В настоящей работе приведены результаты исследования зависимости прямого падения напряжения силового диода при гамма- и электронном воздействии.

Исследуемые образцы представляют собой высокочастотные диффузионные диоды с р⁺-р-n-n⁺- переходом с толщиной базовой области ~200 мкм из кремния КЭФ-4 Ом∙см [1].

Радиационному воздействию подвергались диоды, имеющие минимальный разброс по основным параметрам до воздействия радиации: прямое падение напряжения U_F =0.75÷0.8 В при прямом токе I_F = 10A, обратный ток I_R ~ 0.5-0.7 мкА и 0.7– 1.0 мкА при обратном напряжении U_R = 100 В и 200 В соответственно, время восстановления обратного сопротивления τ_rr ≤ 2.8±0.2∙10^-6 с при I_F = 1A, I_F/I_R = 1 и уровне отсчёта обратного тока 0,1 А. Каждому уровню радиационного воздействия подвергалась группа диодов в количестве 10шт.

Рассмотрим вопрос о возможности расчётного прогнозирования дозовой зависимости прямого падения напряжения на диоде.

В общем виде, прямое падение напряжения на диоде определяется формулой:

U_f = U_б + U_k (1)

В формуле (1): U_б- падение напряжения на базе диода, и U_k - падение напряжения на p-n переходе и n+n контакте.

Расчет величины U_k с учётом падения напряжения на nn+ переходе наиболее полно описан в [2] и в дальнейшем мы будем пользоваться результатами этой работы.

Наиболее сложно обстоит ситуация с расчётом падения напряжения на базе диода. Основная проблема здесь заключается в том, что в процессе облучения меняется соотношение между шириной базы диода (d) и диффузионной длиной неравновесных носителей заряда (L_p). Это приводит во-первых, к тому, что для разных уровней облучения меняется расчётная модель (см., например, [3]), а во-вторых, при определённых уровнях облучения необходимо учитывать наличие в базе диода собственных равновесных носителей (n_o), определяемых её удельным сопротивлением (ρ_б).

К сожалению, в наиболее полной монографии [2], посвящённой этому вопросу, рассматриваются только случаи высокого уровня инъекции во всей базе диода и величина n_o в конечных формулах для U_б не учитывается.

Исходя из этого, в рамках настоящей работы был произведён расчет величины U_б при следующих упрощающих предположениях:

- инъектирующая способность контактов p+n и n+n одинакова, граничные концентрации в плоскостях их расположения равны друг другу и их можно рассчитывать (для прямого тока I_F = 10А) по формуле (2),

Δn ≈	IFLp	=	IF(Dp τp)^0.5	=	IF	≈	4*10^18(KtФ)^-0.5 (2)
	qDpSpn		qDpSpn		q(Dp)^0.5(KtФ)^0.5Spn

где: I_F = 1А – прямой ток, с которого происходит переключение на обратное напряжение при измерении τ_rr,, D_p≈10см²/сек - коэффициент диффузии дырок, L_p – диффузионная длина дырок в базе диода, τ_p ≈ (K_tФ)^-1– время жизни неосновных носителей заряда в базе диода, изменяющееся под действием облучения с потоком Ф, S_pn ≈ 0.5 см² – площадь p-n перехода исследуемых диодов,

- n₀≈1.25*10¹⁵см^-3- концентрация основных носителей в базе при ρ_б~4 ом*см,

- тепловая скорость дырок вычислялась по известной формуле V_p=(3kT/m_p)^0.5 .

Для температуры 300 ºK V_p ≈ 1.58•10⁷ см/сек (при расчёте принималось [4] , что m_p – эффективные масса дырок, равна 0.55m₀, где m₀ – масса покоя электрона),

- если, как об этом говорилось выше, мы принимаем, что время жизни неосновных носителей заряда в базе диода в результате гамма- и электронного облучения формируется А-центром [5-10], то n₁ =N_cexp(-0.17/kT) = 4.05*10¹⁶см^-3 ( для расчёта n₁ использовались значения Nc≈2.8*10¹⁹см^-3, kT ≈ 0.0256 eV из [4]),

- во всей базе диода выполняется закон нейтральности: p_n0 + Δp = n_n0 + Δn,

- распределение концентраций неравновесных носителей по координате в базе диода симметрично относительно середины базы и описывается экспоненциальными функциями вида Δp(x) ≈ Δp(0)*exp(-x/L_p) и Δp(x) ≈ Δp(d)*exp[(x-d)/L_p] со стороны p-n перехода и со стороны nn+ контакта соответственно.

С учётом сделанных предположений и в приближении, достаточном для инженерных расчётов, можно считать, что

U_б ≈ U_{б(0 – d/2)}+ U_{б(d/2 – d)} ≈ 2•U_{б(0 – d/2)} (3)

В формуле (3): U_{б(0 – d/2)} – падение напряжения на участке базы 0 – d/2 (падение напряжения на половине ширины базы, примыкающей к p-n переходу, U_{б(d/2 – d)} падение напряжения на участке базы d/2 – d (падение напряжения на половине ширины базы, примыкающей к n+-n контакту.

С учётом сделанных предположений можно получить следующее выражение для падения напряжения на толще базы p+nn+ диода (U_б):

Uб=	Uбro•	(1-	2Lp	Ln	b•no	+1	) (4)
					(b+1)•p(0)
			d		b•no	+ e^-d/2L
					(b+1)•p(0)

В формуле (4) U_бro – падение напряжения на немодулированной базе диода:

U_бro = (I_f•ρ_б•d)/S_pn (5)

Для расчётов по формулам (1) и (4) необходимо знать численную зависимость времени жизни неравновесных дырок от дозы облучения. Её можно рассчитать по формулам (1) и (2) для величины прямого тока I_F = 10А.

Величина коэффициента радиационного изменения времени жизни(Kτ) вычислялась из известной формулы, определяющей изменение Τ_p под действием радиационного облучения:

1/τ_p(Ф) - 1/τ_p(0) = Δ(1/τ_p) = K_τФ (6),

В формуле (1): τ_p(Ф) – время жизни неосновных носителей заряда после радиационного воздействия Ф, τ(0) - время жизни неосновных носителей заряда до облучения, Kτ – коэффициент радиационного изменения времени жизни.

Экспериментальные данные, их анализ и обсуждение

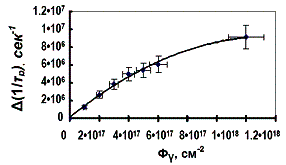
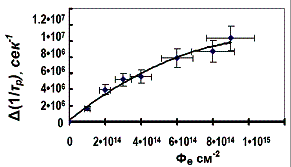
На рис. 1а,б представлены экспериментальные зависимости Δ[1/tp](Ф_γ) и Δ[1/tp](Фе), полученные в настоящей работе. При этом каждой экспериментальной точке сопоставлен наблюдавшийся разброс значений Δ[1/tp] и возможная погрешность определения Ф_γ и Фе (потоков гамма-квантов и электронов, соответственно).

б) зависимость	в) зависимость
Рис. 1. Зависимости времени жизни от дозы облучения р^+рnn^+диода

Из этих рисунков следует, что, что зависимость Δ(1/τ_p) = F(Ф) для диффузионных диодов с геометрией и параметрами, приведёнными выше, в отличие от этой зависимости для планарных приборов, исследованных в [11], явно нелинейная: с величина dF/dФ при увеличении Ф уменьшается. Это по сути означает, что с ростом Ф уменьшается величина коэффициента Kτ (при линейной зависимости Δ(1/τ_p) = F(Ф) Kτ - величина постоянная,

Подобная нелинейная зависимость Δ(1/τ_p) = F(Ф) для диффузионных диодов наблюдалась и анализировалась в работе [8] (для диодов, подвергнувшихся гамма-облучению) и в работе [7] для диодов, подвергнувшихся электронному облучению. В последней работе никакого объяснения этому эффекту не приводится, а в [8] вслед за работой [12] предполагается, что наиболее вероятной причиной наблюдаемой зависимости Δ(1/τ_p) = F(Ф) является снижение скорости введения А-центра с увеличением потока радиации (Ф), воздействующего на диод.

В соответствии с работой [12], уменьшение Kτ «может быть связано с тем, что при больших потоках радиации происходит аннигиляция пар Френкеля на дефектных центрах, в качестве которых могут выступать примеси (контролируемые и неконтролируемые)», которыми, конечно, насыщена база диффузионного диода после высокотемпературной диффузии. Однако, никаких количественных оценок, подтверждающих эту гипотезу, ни в [8], ни в [12] не приводится.

В связи с этим, представляет несомненный интерес разработка (на основе вышеприведённых экспериментальных данных), инженерной методики расчёта зависимостей Δ(1/τ_p) = F(Ф) и(или) Kτ(Ф). При этом будем исходить из двух основополагающих предпосылок достаточно хорошо обоснованных и описанных в литературе:

- величину времени жизни неравновесных носителей заряда (τ_p) в нейтральной базе диода после облучения электронами и гамма-квантами определяет однозарядный А-центр [5-10, 3] ;

- процессы рекомбинации носителей через А-центр происходят в соответствии с теорией рекомбинации Шокли-Рида [8,10].

В соответствии с вышеуказанной теорией, для рекомбинационного центра расположенного в верхней половине запрещённой зоны, константа повреждаемости времени жизни K_t для полупроводника n-типа определяется следующей формулой:

Kt =	(1+Δn/n0)	•Vpσp•	dM	(7)
	(1+Vpσp/Vnσn)•Δn/n0+n1/n0		dФ

В формуле (7): Δn – концентрация неравновесных носителей, n₀ – концентрация равновесных носителей, n₁ – концентрация носителей в зоне проводимости, в случае, если энергетическое положение уровня Ферми совпадает с энергетическим положением рекомбинационного уровня (~0.17 эВ для нашего случая), V_p,V_n – тепловая скорость дырок и электрионов соответственно, σ_p – сечение захвата дырок на рекомбинационный уровень, dM/dФ – скорость введения рекомбинационного центра при облучении.

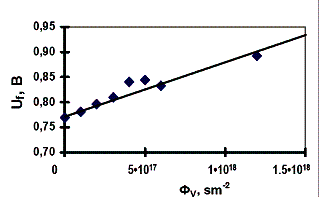
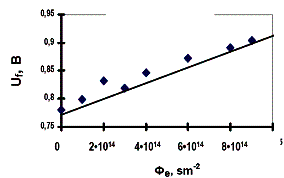
Результаты расчета падения напряжения на диоде (U_f) по вышеприведённым формулам представлена на рис. 2а,б для гамма- и электронного облучения соответственно. Из этих рисунков следует, что предложенная инженерная методика расчета дозовой зависимости прямого падения напряжения достаточно точно описывает экспериментальную зависимость и этой методикой можно пользоваться для прогнозирования влияния гамма- и электронного излучения на прямое падение напряжения кремниевых диффузионных диодов.

Рис. 2. Зависимость Uf = F(Фγ) и Uf = F(Фе)- расчёт по формулам (3) и (5) - экспериментальные точки

Таким образом, предложена и разработана инженерная методика расчёта прямого падения напряжения на диоде (с использованием разработанного метода расчёта Kτ), которая удовлетворительно объясняет полученные экспериментальные данные.

Литература:

1. Рахматов А.З., Каримов А.В., Сандлер Л.С., Ёдгорова Д.М., Скорняков С.П. Влияние гамма- и электронного облучения на ключевые параметры мощных высокочастотных диффузионных диодов. Компоненты и технологии. Санкт-Петербург, 2013. № 10. С.140-142.

2. Э.И. Адирович, П.М. Карагергий-Алкалаев, А.Ю. Лейдерман. Токи двойной инжекции в полупроводниках. Советское Радио, г. Москва, 1978 г., стр. 61, 65.

3. И.П.Степаненко. Основы теории транзисторов и транзисторных схем Энергия, Москва, 1977 г. стр. 142, 143.

4. Л. Россадо. Физическая электроника и микроэлектроника Перевод с испанского, Высшая школа, г. Москва, 1991 г. стр. 321, 322.

5. Е.А. Ладыгин. Радиационная технология твёрдотельных электронных приборов, Москва, 1976 г., стрю 118 – 124, 218-234, 48.

6. Ф.П. Коршунов и др. Радиационные эффекты в полупроводниковых приборах, Минск, Наука и техника, 1978 г., стр. 55 – 81.

7. В.С. Вавилов, Н.А. Ухин. Радиационные эффекты в полупроводниках и полупроводниковых приборах, Атомиздат, г. Москва, 1969 г., стр. 208 – 231.

8. Ю.М. Добровинский. Исследование радиационных эффектов в диффузионных элетронно-дырочных переходах на основе кремния. Разработка гамма-радиационного технологического процесса. Диссертация на соискание учёной степени кандидата физико-математических наук. г. Ташкент, 1981 г., стр. 59, 67-68, 61, 133.

9. В.М. Кулаков, Е.А. Ладыгин, В.И. Шаховцов Действие проникающей радиации на изделия электронной техники, г. Москва, Советское радио, 1980 г., стр. 121 – 142.

10. А.С.Зубрилов, С.В.Кавешников Влияние примесного состава n-кремния на радиационное дефектообразование и деградацию времени жизни ннз при гамма-облучении, ФТП, т.25, вып. 8, 1991 гш., стр. 1332 – 1338.

11. А.З. Рахматов, М.Ю. Ташметов, Л.С. Сандлер. Влияние проникающей радиации на параметры высоковольтных планарных выпрямительных диодов Вопросы атомной науки и техники, серия Физика радиационных повреждений и радиационное материаловедение(98), № 4 2011 г., стр. 26 – 33.

12. Болотов В.А., Васильев В.А., Двуреченский А.В. Вопросы радиационной технологии полупроводников, Наука, г. Новосибирск, 1980 г., стр. 256.