к.ф.-м.н.
Пчелинцева Е.С., к.т.н. Новиков. С.Г., Беринцев А.Н.,
д.ф.-м.н.
Костишко Б.М., д.ф.-м.н. Светухин В.В., Федоров И.С.
Ульяновский
государственный университет, Россия
Физическая модель
преобразования энергии ионизирующего излучения в электрическую
Аннотация. В работе разработана физическая модель преобразования
энергии ионизирующего излучения в электрическую для
радиационно-стимулированного источника электрического питания на основе 63Ni.
Ключевые слова: бетавольтаический эффект; радиационно-стимулированная
генерация тока, эффект аномального фотонапряжения.
Работа
выполнена при поддержке Госкорпорации «Росатом» ГК № H.4б.43.9Б.14.1061
Введение
В большинстве своем радиационно-стимулированные
источники электрической энергии представляют собой два связанных компонента -
радиоизотопный бета-источник и полупроводниковый преобразователь [1].
При физическом и
математическом моделировании работы радиационно-стимулированные источники
электрической энергии важно провести анализ трех основных процессов –
взаимодействие бета излучения с полупроводниковой структурой, разделение
генерированных носителей заряда и формирование выходного напряжения. Рассмотрим
эти процессы на примере радиоизотопного источника, выполненного в виде фольги и
расположенного над поверхностью поликристаллического структурированного
преобразователя с эффектом аномального напряжения (АН) [2].
Постановка задачи
Целью данной работы являлось разработка физической модели
преобразования энергии ионизирующего излучения в электрическую для
радиационно-стимулированного источника электрического питания на основе 63Ni с повышенным значением выходного напряжения.
Результаты
В качестве базовой модели
для исследования бетавольтаического эффекта была выбрана структура
микрокристаллита с p − n−переходом в составе поликристаллической
структурированной АН-пленки (рис.1).
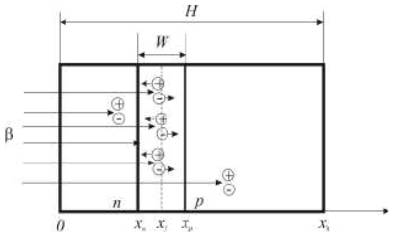
β–
бета частица излученная радиоактивным изотопом, xn−ширина
ОПЗ в полупроводнике n−типа проводимости, xp−ширина
ОПЗ в полупроводнике p−типа проводимости, xf−металлургическая
граница перехода, W−ширина области пространственного заряда, H−толщина
микрокристаллитаРисунок 1 – Структура микрокристаллита с p −
n−переходом под воздействием облучения.
Процессы движения бета
частиц в полупроводниковых материалах, используемых в составе бетавольтаических
элементов, обычно рассматриваются при помощи метода Монте-Карло [3]. Из этого
анализа следует, что соотношение между энерговыделением и глубиной
проникновения бета-частиц можно выразить в следующем виде [4]:
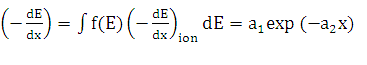 (1),
(1),
где f(E) – вероятность излучения бета частицы с энергией
E, a1 и a2 – поправочные коэффициенты, зависящие от
физических свойств и геометрической конфигурации устройства.
Для определения выражения
для плотности тока, генерируемого под воздействием бета-излучения в структуре
одного микрокристаллита можно воспользоваться уравнением непрерывности, для
неосновных носителей в p− и n−областях [3, 4, 5]. В области
n−типа уравнение непрерывности для неосновных носителей запишется в
следующем виде:
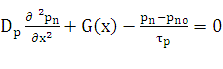 (2),
(2),
где pn и pn0 – концентрации дырок
при воздействии бета-частиц и без него соответственно; Dp−
коэффициент диффузии дырок; G(x) – коэффициент генерации электронно-дырочных
пар, который определяется по формуле:
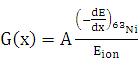 (3),
(3),
где A−активность 63Ni, Eion −
средняя энергия потраченная на создание одной электронно-дырочной пары в
поглотителе.
С учетом уравнения (1)
коэффициент G(x)
может быть выражен следующим образом:
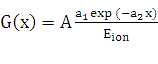 (4)
(4)
Для поиска решения данного
уравнения необходимо определить граничные условия.
1) На внешнем контакте, при
x = 0 изменение концентрации неосновных носителей заряда характеризуется
повышенной скоростью поверхностной рекомбинации Sp:
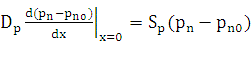 (5)
(5)
2) На границе x=хn
(рис. 1) отсутствует избыток неосновных носителей заряда, вызванный ионизацией:
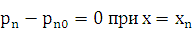
Для p−области,
уравнение непрерывности и граничные условия можно записать в следующем виде:
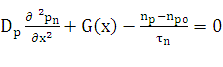 (6)
(6)
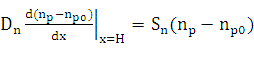 (7)
(7)
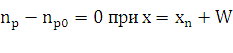 (8)
(8)
где Dn− коэффициент диффузии электронов,
Sn−скорость поверхностной рекомбинации электронов, tn−время
жизни носителя заряда, np− и np0−концентрации
электронов в p−области под воздействием бета-излучения и без него
соответственно.
В результате расчетов
суммарный радиационно-индуцированный ток является суммой токов генерируемых в
n− и p−областях, а также в области пространственного заряда и
выражается следующим образом.
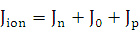 (9)
(9)
Напряжение холостого хода
для одного микрокристаллита выражается следующим уравнением [5]:
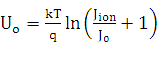 (10)
(10)
С целью повышения
эффективности преобразования энергии радиоактивного распада в электрическую
энергию, в данной модели использовать эффект АН, которое наблюдается в
поликристаллических пленках на основе различных материалов.
Максимальное напряжение в
АН структуре может достигать значений порядка mUo (2m−число p
− n−переходов). Однако на практике, из-за значительных отличий
модельных свойств переходов, наличия барьеров на границах микрокристаллитов
напряжения будут существенно отличаться от теоретических.
Более того, поскольку
кристаллиты имеют размеры порядка 104 − 105 см, то
вопрос о соотношении размера кристаллита H и длины диффузионного смещения L
показывает возможность взаимодействия соседних p −
n−переходов между собой [6], что может значительно уменьшить значение
выходного напряжения.
Разность значений
напряжения на соседних переходах Uoj и
Uoj+1
позволит определить значение общего выходного напряжения поликристаллической
структуры в виде:
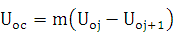 (11)
(11)
В указанном приближении,
зависимость функции энерговыделения, и собственно коэффициентов генерации в
пределах одного периода (и для двух взаимодействующих переходов) можно считать
линейной в зависимости от координаты вдоль поверхности поликристаллической
пленки.
Напряжение на выходе источника в зависимости от
активности источника, полученные в результате математического моделирования
приведены на рис.2. Данные зависимости получены при рассмотрения
поликристаллических пленок с ориентированными микрокристаллитами, плотность
которых составляет 104 на сантиметр.
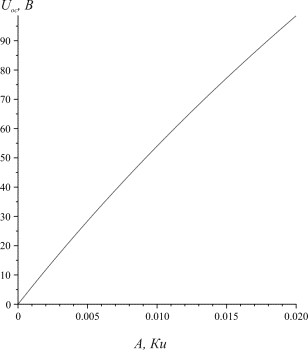
Рисунок 2 – Зависимость выходного напряжения холостого
хода источника электрического питания на основе изотопа 63Ni.
Таким образом, в данной
работе разработана физическая модель выходного напряжения преобразователя
энергии ионизирующего излучения в электрическую на основе поликристаллической
пленки с АН.
Список
литературы
1.
Импульсные
радиационно-стимулированные источник электрического питания / Е.С. Пчелинцева,
С. Г. Новиков, А. В. Беринцев и др. // Известия самарского научного центра РАН.
2012. Т. 14, № 4. С. 1126–1128.
2. Johnson H. R., Williams R. H., Mee C. H. B. The anomalous photovoltaic effect in cadmium telluride // Journal of Physics D: Applied Physics. 1975.
Vol. 8, no. 13. P. 1530–1541.
3. ZUO Guoping, ZHOU Jianliang, KE Guotu. A simple theoretical model for
63ni betavoltaic battery // Applied Radiation and Isotopes. 2013. Vol. 82, no.
0. P. 119 – 125.
4. ZUO Guoping, ZHOU Jianliang, KE Guotu. A simple theoretical model for
63ni betavoltaic battery // Applied Radiation and Isotopes. 2013. Vol. 82, no.
0. P. 119 – 125.
5. Design and simulation of betavoltaic battery using large-grain
polysilicon / Shulin Yao, Zijun Song, Xiang Wang et al. // Applied Radiation
and Isotopes. 2012. Vol. 70, no. 10. P. 2388 – 2394.
6. Wei Lawrence S. Parametric studies and optimization of the beta-voltaic
cell-ii open-circuit voltage and power efficiencies // Solid-State
Electronics. 1975. Vol. 18, no. 1. P. 71 – 77