Технические науки/2. Механика

 

Аспирант Агарков А.М.,

студент Краснов В.В., студент Локтионов И.С.

Белгородский государственный технологический

университет им. В.Г. Шухова, Россия

 

Расчет объёмов аспирируемого воздуха

 

Используя динамический подход к определению объемов эжектируемого воздуха, изложенный в работах О.Д. Нейкова, И.Н. Логачева и В.А. Минко, а также результаты проведенных аналитических и экспериментальных исследований аэродинамики рециркуляционных систем была разработана методика расчета объёмов аспирируемого воздуха, позволяющая учесть как влияние перегружаемого материала, так и подачу рециркуляционного потока, на процесс движения эжектируемого воздуха в перегрузочном желобе.

Основу предлагаемой методики составляют известные расчетные зависимости объемов эжектируемого воздуха для обычных аспирационных систем (АС), важнейшим параметром которых является суммарный КМС тракта "вернее укрытие – желоб – нижнее укрытие". В нашем случае  воздействие рециркуляционного потока на процесс эжектирования учитывается выражением (4.8).

Исходными данными при выполнении расчета являются.

1. Характеристика перегружаемого материала: расход Gм; плотность rм; гранулометрический состав, определяемый ситовым методом.

2. Характеристика перегрузочного узла: схема узла с углами наклона желоба к горизонту и высотами падения материала; площадь поперечного сечения желоба Sж; тип аспирационного укрытия; площади неплотностей верхнего Fву и нижнего Fну  укрытий.

Расчет объёмов аспирации ведется в следующей последовательности.

1. Рассчитывается скорость потока перегружаемого материала при выходе из желоба Vк в нижнее укрытие путем последовательного расчета движения материала на всех прямолинейных участках желоба:

а) для вертикальных участков

Vk = Ö Vн 2  + 2gh    ,                                                  (1)

б) для наклонных участков

                              Vk = Ö (Vн  sina)2 +2 gh(1-0,5×ctga)   ,                              (2)

где h – высота падения материала;

      Vн – скорость движения материала в начале желоба;

      a – угол наклона желоба к горизонту.

Для перегрузочного желоба изображенного на рис. 1. скорость Vк будет определяться следующим образом:

а) скорость в начале желоба

                       Vн = Vк1 =Ö 2 g h1    ,                                                 (3)

б) скорость на выходе из вертикального участка желоба

                       Vк2 = Ö V1 2 + 2gh22     ,                                               (4)

в) скорость в конце желоба

                       Vк = Vк3 = Ö (Vк2×sina ) 2 + 2g×h3 ( 1 – 0,5×ctga )   .                 (5)

2. Объемная концентрация частиц материала в желобе

                                  b = 2 Gн / (rм Sж (1+ n) Vк )    ,                                     (6)

где n = Vн / Vк – отношение скоростей потока частиц в начале  и конце желоба.

3. Средний диаметр частиц перегружаемого материала, мм

                                d = 0,01 Ni × di     ,                                               (7)

где Ni – процентное содержание (по массе) частиц диаметром di .

Если d £ 14,6b 0,5, то следует принять в качестве расчетного среднего диаметра  d = 14,6 b 0,5.

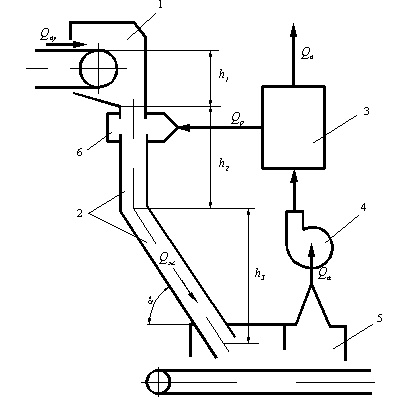
C:\DISSERTACIA\RIS\ris_4_1.wmf

Рис. 1. Схема рециркуляционной  системы аспирации перегрузочного узла: 1 – верхнее укрытие; 2 – желоб; 3 – пылеконцентратор; 4 – вентилятор; 5 – нижнее укрытие; 6 – воздушный затвор

 

4. Сумма коэффициентов местных сопротивлений желоба и укрытий аспирационной системы

                                åx = xж + xну + xвз + ( 1 - q )2 × xву  ,                             (8)

где xж , xвз , xну , xву – КМС желоба, воздушного затвора, нижнего и верхнего укрытий, q  – относительный расход рециркуляционного воздуха.

Для вертикальных желобов xж = 1,5, для желобов с наклонным участком xж=2,5.

Для укрытий с жесткой внутренней перегородкой величина xну зависит от отношения площади поперечного сечения желоба к площади перегородки Sж / Sп и отношения высоты перегородки к высоте укрытия Нп / Ну. Значение xну для укрытий данного типа представлены в табл. 1. Для укрытий без внутренней, жесткой перегородки xну = 0 .

Величина xву рассчитывается исходя  из площадей желоба Sж и неплотностей верхнего укрытия Fву

                                  xву = 2,4 ( S ж / Fву )2  .                                           (9)

Значение xвз зависит  как от относительного расхода рециркуляционного воздуха q (рис. 2), так  и от отношения площадей щели воздушного затвора и желоба  f = Sвз /Sж .

Как показали проведённые исследования одним из параметров, существенно влияющих на гидравлическое сопротивление  тракта "верхнее  укрытие – желоб – нижнее укрытие", а следовательно, и на аэродинамические характеристики АС с принудительной рециркуляцией, является относительный расход рециркуляционного воздуха  q .

Величина q должна обеспечивать наименьшие объёмы эжектируемого воздуха и выброса аспирационной системы. Порядок определения оптимальной величины q будет рассмотрен несколько ниже.

                                                                                                  Таблица 1.

Значения xну  для укрытий с двойными стенками и внутренней перегородкой

 

Sж/S п

Нп / Ну

0,1

0,2

0,3

0,4

0,5

1,0

0,8

0,6

0,4

0,2

0,1

193

124

69,5

30,9

7,72

1,93

44,5

28,5

16,0

7,12

1,78

0,45

17,8

11,4

6,41

2,84

0,71

0,18

8,12

6,19

2,92

1,3

0,32

0,08

4,02

2,57

1,45

0,64

0,16

0,04

   

4. Коэффициент лобового сопротивления частицы

y = 1,8 exp [-1,8( b × 103 ) 0,5 / d ] .                         (10)

5. Число Бутакова – Нейкова

Вu = 1,5y× Vк × Gм / (g × d ×10-3 × rм × Sж  × å x )  .                  (11)

По формуле (4.11) вычисляется число Вu  для вертикальных и желобов с преобладанием вертикальных участков. Для наклонных желобов ускорение свободного падения g в данном выражении необходимо заменить на ускорение движения материала

а = g× sina (1- fтр× ctga ) ,                                      (12)

где fтр » 0,5 – коэффициент трения материала о днище желоба.

 6. Значение критерия Эйлера

Eu =  2Pу / rв× Vк2×åx    ,                                    (13)

где Ру – величина разряжения в нижнем укрытии,

      rв – плотность аспирируемого воздуха.

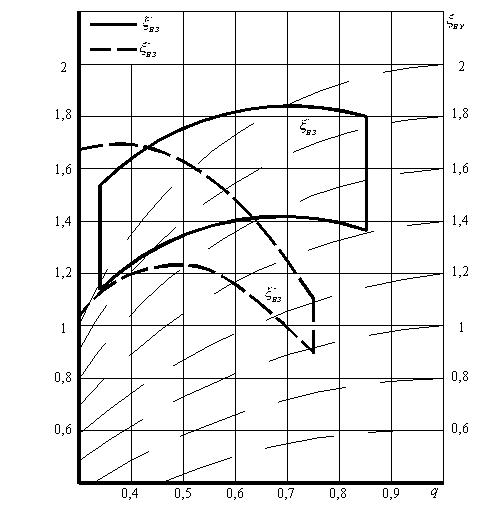
C:\DISSERTACIA\RIS\ris_4_2.wmf

   Рис. 2.  Поля значений КМС воздушных затворов и величины q×(2-q)×xву

 

При аспирации технологического оборудования, обладающего вентилирующей способностью (валковые и молотковые дробилки, дезинтеграторы), к разряжению  в укрытии необходимо добавить величину давления Роб, развиваемого рабочими органами оборудования. Выражение (13) в этом случае примет следующий вид

Eu = 2( Pу + Pоб ) / rв × Vк2 ×åx   .                              (14)

7. При найденных числах Ви и Еи коэффициент скольжения компонентов для равномерно ускоренного потока частиц определяется по формуле

j = Ö 0,33 Ви [|1-j|3 - | n -j |3] + Еи    .                     (15)

Решение данного уравнения можно найти методом последовательных приближений, полагая в качестве первого приближения

j1 = 0,5 [0,5 ( 1+ n ) + Еи0.5]  .                                (16)

Если окажется, что j1 < n, то величина j определяется решением квадратного уравнения (полученного из (15), опуская знаки абсолютной величины и раскрывая скобки):

j = Ö [ b/(2a) ]2 + c/a  -  b/(2a) ,                                 (17)

где:                                        а = 1 - Вu   (1 - n)   ;                                           (18)

b = (1 + n 2) × Вu  ;                                              (19)

c =  Eu + Вu × (1- n3) / 3 .                                          (20)

8. Расход воздуха, поступающего в нижнее укрытие по желобу

Qж = j × Vк× Sж × (1- b )2  ,                                      (21)

9. Расход воздуха, поступающий в нижнее укрытие через неплотности

Qн = 0,65× FнуÖ 2×Pу  /rв     ,                                       (22)

где Fну – площадь неплотностей нижнего укрытия.

10. Расход  аспирируемого воздуха

Qа= Qж + Qн ,                                                  (23)

11. Расход воздуха  в линии рециркуляции аспирационной системы

Qр= q × Qж  ,                                                      (24)

12. Расход воздуха, поступающий через неплотности верхнего укрытия

Qву = (1- q)× Qж  ,                                                 (25)

должен предотвращать возможность выбивания пыли через неплотности

Полученные расходы воздуха в трубопроводах АС позволяют произвести их гидравлический расчёт.

Величина давления, затрачиваемого на преодоление гидравлического сопротивления линии рециркуляции, включающего сопротивление распределителя рециркуляционного потока, определяется аэродинамическими характеристиками, применяемого пылеконцентратора и величенной потерь  давления в трубопроводе выброса аспирационной системы.

Как отмечалось выше, одним из важнейших компонентов расчета объёмов аспирации АС с принудительной рециркуляцией является оптимальная величина относительного расхода q.

Снижения объемов эжекции за счет роста гидравлического сопротивления желоба на величину, обуславливаемую действием воздушного затвора, можно записать следующим образом

xвз - q×(2- q)×xву = Dx   ,                                           (26)

где Dx – разность суммарных КМС рециркуляционной и обычной АС.

Величину Dx можно определить при помощи полей значений КМС воздушных затворов и величины q× (2- q)×xву  (рис. 2).

Анализ выражений (21), (15), (13) и (11) показывает, что наибольшее снижение объемов эжектируемого воздуха Qж будет иметь место при максимально-возможной положительной величине Dx .  Причем указанный максимум имеет место при минимальных значениях относительного расхода q (рис.2.).

С другой  стороны  снижение q  влечет  за собой повышенный  выброс в атмосферный воздух

Qв = (1- q)× Qж + Qн ,                                             (27)