Любимова А.А.

 Южно-Уральский государственный университет филиал в г. Златоусте

Численное интегрирование с помощью квадратурных формул Гаусса

Численное интегрирование —  это вычисление значения определённого интеграла (как правило, приближённое). Оно применяется, когда:

1.                      Сама подынтегральная функция не задана аналитически. Например,   представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.

2.                      Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции.

  Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы вида (1):

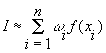,                                           (1)

где n - число точек, в которых вычисляется значение подынтегральной функции, точки  называются узлами метода, числа  - весами узлов.

Рассмотрим интегрирование функций с использованием формул Гаусса, обладающих наивысшей алгебраической точностью. Задача состоит в том, чтобы подобрать точки   и коэффициенты  так, чтобы квадратурная формула 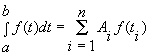(2)

                                                                                         (2)

была точной для всех полиномов наивысшей возможной степени.

         Ввиду того, что имеется  параметров и   , а полином степени   определяется  коэффициентами, эта наивысшая степень в

общем случае .

Запишем полином в виде 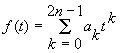 и подставим в (2). Получим

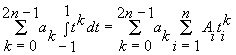                                      .                                    (3)

Приравнивая выражения при одинаковых коэффициентах , получим

,      ,

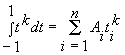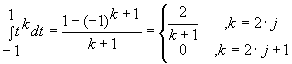                   ,                         (4)

Итак, и   находят из системы  уравнений

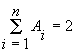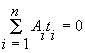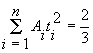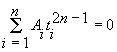                   ,    ,      …  .           (5)

Формулу 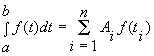, в которой - нули полинома Лежандр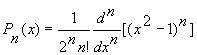а  , а  определяют из (6), называют квадратурной формулой Гаусса.

                                                                     (6)

Делая замену переменной

,                                                  (7)

 

получим:

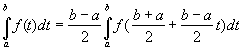                                      .                                  (8)

Применяя к последнему интегралу квадратурную формулу Гаусса, будем иметь:

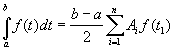.                              (9)

В общем случае формула имеет вид:

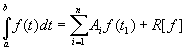                                            ,                               (10)

где - остаточный член.

Остаточный член формулы Гаусса с узлами выражается формулой (11):

    .                               (11)

Приближенные значения абсцисс  и коэффициентов  в квадратурной формуле Гаусса представлены в таблице 1.

Таблица 1

n

I

1

1

0

2

2

1, 2

0,57735027

1

3

1, 3

2

0,77459667

0

0,55555555

0,88888888

4

1, 4

2, 3

0,86113631

0,33998104

0,34785484

0,65214516

5

1, 5

2, 4

3

0,90617985

0,53846931

0

0,23692688

0,47862868

0,56888889

Рассмотрим решение интеграла с  помощью квадратурных формул Гаусса для случая трех ординат на конкретном примере: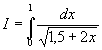

Начальные условия  и . В силу формулы замены переменной и таблицы 1 абсциссы точек будут иметь следующие значения (12):

  ,   ,   ,             (12)

, , .

Для оценки остаточной погрешности  воспользуемся формулой (13):

                            ,   .              (13)

         Следовательно  .

         Несмотря на высокую точность квадратурных формул Гаусса, ими пользуются сравнительно редко из-за трудностей при расчетах. Поэтому специально была реализована программа  в среде MatLab (рис. 1).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Рис. 1 Реализация программы решения интеграла с помощью квадратурных формул Гаусса

 

Литература:

1.                 Блюмин А.Г., Федотов А.А., Храпов П.В.Численные методы вычисления интегралов и решения задач для обыкновенных дифференциальных уравнений. Методические указания к выполнению лабораторных работ по курсу «Численные методы». - М.: Московский государственный технический университет им. Н.Э.Баумана, 2008. – 74 с.

2.                 Демидович Б.П., Марон И.А. Основы вычислительной математики. Изд. 3-е, испр. — М.: Наука, 1966. — 664 с.