Математика/1. Дифференциальные и интегральные уравнения
Ву Н. Ш. Т., к. ф.-м. н. Прядиев В. Л.
Белгородский
государственный национальный исследовательский университет
Некоторые классы естественных условий
в задаче Штурма-Лиувилля на графе
Введение.
Известно (см., например,
[1]), что функция ![]() ,
, ![]() , минимизирующая функционал
, минимизирующая функционал
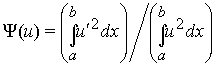
на множестве ![]() , удовлетворяет не только дифференциальному уравнению
, удовлетворяет не только дифференциальному уравнению ![]() , где
, где ![]() , но и краевым условиям
, но и краевым условиям ![]() ,
, ![]() . Эти краевые условия называются естественными. Знание
вида естественных условий позволяет получать оценки на собственные значения
соответствующей задачи Штурма-Лиувилля, что в случае функционала более общего
вида, нежели
. Эти краевые условия называются естественными. Знание
вида естественных условий позволяет получать оценки на собственные значения
соответствующей задачи Штурма-Лиувилля, что в случае функционала более общего
вида, нежели ![]() , может оказаться полезным в приложениях.
, может оказаться полезным в приложениях.
В настоящей статье
рассматривается функционал
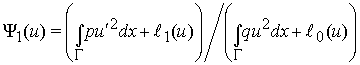 , (1)
, (1)
где ![]() – геометрический
граф,
– геометрический
граф, ![]() и
и ![]() – некоторые
положительные функции, а
– некоторые
положительные функции, а ![]() и
и ![]() – квадратичные формы
относительно значений
– квадратичные формы
относительно значений ![]() и
и ![]() в вершинах
в вершинах ![]() . Изучается вопрос о виде естественных условий, которым
должна удовлетворять функция
. Изучается вопрос о виде естественных условий, которым
должна удовлетворять функция ![]() , минимизирующая функционал
, минимизирующая функционал ![]() . При этом рассматриваются два класса функций, на которых
минимизируется
. При этом рассматриваются два класса функций, на которых
минимизируется ![]() : класс функций, непрерывных на
: класс функций, непрерывных на ![]() , и класс функций, допускающих разрывы в вершинах
, и класс функций, допускающих разрывы в вершинах ![]() .
.
1. Общие понятия и факты.
Начнём с понятия геометрического графа. Под
геометрическим графом мы понимаем связное множество ![]() , представимое в виде
, представимое в виде 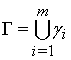 , где
, где ![]() ,
, ![]() , – прямолинейные отрезки. При этом будем предполагать, что
при
, – прямолинейные отрезки. При этом будем предполагать, что
при ![]() ,
, ![]() , где через
, где через ![]() обозначено множество
концевых точек отрезка
обозначено множество
концевых точек отрезка ![]() ,
, ![]() .
.
Пусть 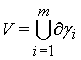 ; точки из
; точки из ![]() называются вершинами
графа
называются вершинами
графа ![]() . Зафиксируем множество
. Зафиксируем множество ![]() такое, что
такое, что ![]() связно. Точки из
связно. Точки из ![]() называются граничными
вершинами
называются граничными
вершинами ![]() , а точки из
, а точки из ![]() называются
внутренними вершинами
называются
внутренними вершинами ![]() . Для любой вершины
. Для любой вершины ![]() через
через ![]() будем обозначать
будем обозначать ![]() |
|
![]() . Ниже, для простоты изложения, будем предполагать всегда,
что к каждой граничной вершине примыкает ровно одно ребро, то есть
. Ниже, для простоты изложения, будем предполагать всегда,
что к каждой граничной вершине примыкает ровно одно ребро, то есть ![]() .
.
Всюду далее
предполагается, что каждое из рёбер графа как-то ориентировано, то есть при
каждом ![]() для каждой из двух
точек множества
для каждой из двух
точек множества ![]() указано какая из них
первая (начало отрезка
указано какая из них
первая (начало отрезка ![]() ), а какая – последняя (конец
), а какая – последняя (конец ![]() ). Договоримся всюду далее начало
). Договоримся всюду далее начало ![]() обозначать через
обозначать через ![]() , а конец – через
, а конец – через ![]() .
.
Будем считать всегда,
что в ![]() задана евклидова
топология, а на
задана евклидова
топология, а на ![]() – топология,
индуцированная из
– топология,
индуцированная из ![]() . Пусть
. Пусть ![]() – множество всех функций,
непрерывных на
– множество всех функций,
непрерывных на ![]() , а
, а ![]() – множество всех
функций
– множество всех
функций ![]() , определённых и непрерывных на
, определённых и непрерывных на ![]() и имеющих конечные
пределы
и имеющих конечные
пределы
![]()
для любой ![]() и любого
и любого ![]() .
.
Производная ![]() функции
функции ![]() в точке
в точке ![]() понимается нами так
же, как и в [2], и так же, как и в [2], через
понимается нами так
же, как и в [2], и так же, как и в [2], через ![]() для
для ![]() и
и ![]() мы обозначаем
производную функции
мы обозначаем
производную функции ![]() в точке
в точке ![]() вдоль ребра
вдоль ребра ![]() в направлении от
в направлении от ![]() . Пусть
. Пусть
![]() и
и ![]() .
.
В дальнейшем мы будем
рассматривать задачу о минимизации функционала (1) только на множествах
![]()
и
![]() .
.
Пусть ![]() – функционал,
определённый на
– функционал,
определённый на ![]() формулой
формулой
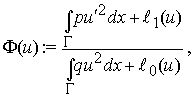 (2)
(2)
где
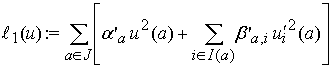 ,
,
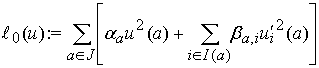 ,
,
а функция ![]() минимизирует
минимизирует ![]() на
на ![]() . Здесь
. Здесь ![]() и
и ![]() положительны, причём
положительны, причём ![]() ,
, ![]() на
на ![]() , а
, а ![]() ,
, ![]() ,
, ![]() ,
, ![]() – некоторые
вещественные числа. Если для
– некоторые
вещественные числа. Если для ![]() существует ненулевой
линейный относительно
существует ненулевой
линейный относительно ![]() и
и ![]() (
(![]() ) функционал
) функционал ![]() такой, что
такой, что ![]() , то условие
, то условие ![]() будем называть естественным
(для пары (
будем называть естественным
(для пары (![]() ,
, ![]() )) в точке
)) в точке ![]() .
.
Аналогично понимается
естественное условие в точке ![]() для пары
для пары ![]() для
для
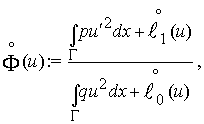
где
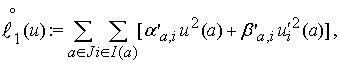
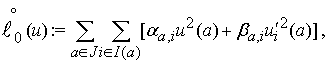
![]() и
и ![]() – те же, что и в (2),
– те же, что и в (2),
![]() ,
, ![]() ,
, ![]() ,
, ![]() – некоторые
вещественные числа.
– некоторые
вещественные числа.
2. Формулировка и доказательство основного
результата.
Теорема 1. Пусть
![]()
где ![]() . Тогда
. Тогда ![]() есть решение
уравнения
есть решение
уравнения
![]() (3)
(3)
и удовлетворяет
естественным условиям
![]() (4)
(4)
и условиям
![]() (5)
(5)
причём набор (по ![]() ) условий (4) и набор тех из условий (5), для которых
) условий (4) и набор тех из условий (5), для которых ![]() , исчерпывают все линейные независимые естественные условия.
, исчерпывают все линейные независимые естественные условия.
Доказательство. В силу определения ![]() имеем
имеем
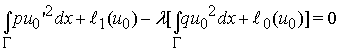 (6)
(6)
и
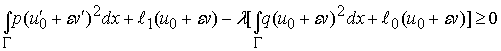 (7)
(7)
для ![]() и достаточно малых
и достаточно малых ![]() . Из (7) в силу (6) следует, что
. Из (7) в силу (6) следует, что
![]() (8)
(8)
для всех ![]() ; здесь
; здесь
![]()
Интегрируя в (8) по
частям получим, что
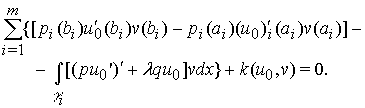 (9)
(9)
Пусть
![]()
Тогда для любого ![]() равенство (9) примет
вид
равенство (9) примет
вид
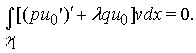
Отсюда по лемме Лагранжа
получим, что
![]() на
на ![]() .
.
Аналогично мы получим,
что ![]() на
на ![]() , на
, на ![]() , ..., на
, ..., на ![]() . Таким образом,
. Таким образом, ![]() есть решение
уравнения (3).
есть решение
уравнения (3).
С учётом этого (9)
принимает вид
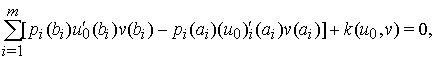
то есть
![]() (10)
(10)
Зафиксируем ![]() и рассмотрим
множество
и рассмотрим
множество
![]() {
{![]() |
| ![]() }
}
При ![]() равенство (10)
принимает вид
равенство (10)
принимает вид
![]() (11)
(11)
Ввиду произвольности ![]() естественность
условий (4) доказана.
естественность
условий (4) доказана.
Подставляя теперь (11) в
(10), получим
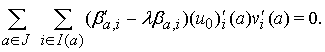 (12)
(12)
Фиксируя ![]() и
и ![]() , рассмотрим множество
, рассмотрим множество ![]() функций
функций ![]() таких, что
таких, что ![]() и
и ![]() , если
, если ![]() или
или ![]() . Для
. Для ![]() равенство (12)
принимает вид
равенство (12)
принимает вид
![]()
Теорема доказана.
Замечание. Если ![]() , то (5) принимает вид
, то (5) принимает вид ![]() .
.
Теорема 2. Пусть
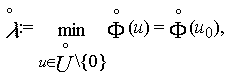
где ![]() . Тогда
. Тогда ![]() есть решение
уравнения
есть решение
уравнения
![]() (13)
(13)
и удовлетворяет естественным
условиям
![]() (14)
(14)
и условиям
![]() (15)
(15)
причём набор условий (14)
и набор тех из условий (15), для которых ![]() , исчерпывают все линейные независимые естественные условия.
, исчерпывают все линейные независимые естественные условия.
Доказательство. В силу определения ![]() имеем
имеем
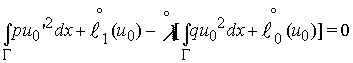 (16)
(16)
и
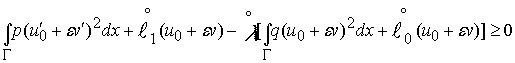 (17)
(17)
для ![]() и достаточно малых
и достаточно малых ![]() . Из (17) в силу (16) следует, что
. Из (17) в силу (16) следует, что
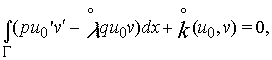 (18)
(18)
для всех ![]() ; здесь
; здесь 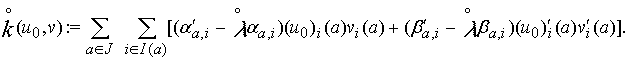
Интегрируя в (18) по
частям получим, что
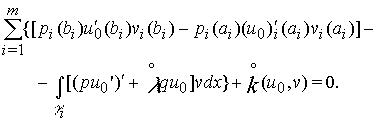 (19)
(19)
Пусть
![]() |
| ![]() }.
}.
Тогда для любого ![]() равенство (19) примет
вид
равенство (19) примет
вид
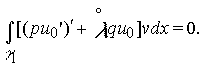
Отсюда по лемме Лагранжа
получим, что
![]() на
на ![]() .
.
Аналогично мы получим,
что ![]() на
на ![]() , на
, на ![]() , ..., на
, ..., на ![]() . Таким образом,
. Таким образом, ![]() есть решение уравнения
(13).
есть решение уравнения
(13).
С учётом этого (19)
принимает вид
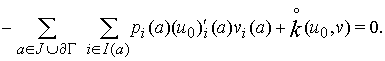 (20)
(20)
Зафиксируем ![]() и
и ![]() и рассмотрим
множество
и рассмотрим
множество 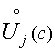 функций
функций ![]() таких, что
таких, что ![]() и
и ![]() , если
, если ![]() или
или ![]() , а также
, а также ![]() для всех
для всех ![]() и
и ![]() . При
. При 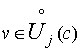 равенство (20)
принимает вид
равенство (20)
принимает вид
![]() (21)
(21)
Ввиду произвольности ![]() естественность
условий (14) доказана.
естественность
условий (14) доказана.
Подставляя теперь (21) в
(20), получим
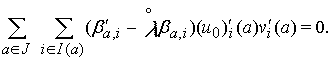 (22)
(22)
Фиксируя ![]() и
и ![]() , рассмотрим множество
, рассмотрим множество 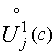 функций
функций ![]() таких, что
таких, что ![]() и
и ![]() , если
, если ![]() или
или ![]() . Для
. Для 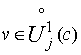 равенство (22)
принимает вид
равенство (22)
принимает вид
![]()
Теорема доказана.
Литература:
1. Гулд
С.
Вариационные методы в задачах о собственных значениях. - М.: Мир, 1966. - 328
с.
2. Покорный
Ю.В., Пенкин О.М., Прядиев В.Л., Боровских А.В., Лазарев К.П., Шабров С.А. Дифференциальные
уравнения на геометрических графах. - М.: ФИЗМАТЛИТ, 2004. - 272с.