к.ф.-м.н. И.А. Долгарев и к.ф.-м.н.
А.И. Долгарев
ЛИНЕЙНЫЕ
ПРОСТРАНСТВА КОРТЕЖЕЙ ЭЛЕМЕНТОВ ПолЯ ГАЛУА, СОСТОЯЩЕГО иЗ ![]() ЭЛЕМЕНтОВ
ЭЛЕМЕНтОВ
Рассмотрено поле Галуа, состоящее из ![]() элементов,
элементов, ![]() простое число. На
кортежах элементов этого поля с использованием нелинейной операции определена
абелева группа. Она содержит элементы, порядки которых больше
простое число. На
кортежах элементов этого поля с использованием нелинейной операции определена
абелева группа. Она содержит элементы, порядки которых больше ![]() . Существует линейное пространство на указанной группе,
отличное от стандартного линейного пространства над полем Галуа.
. Существует линейное пространство на указанной группе,
отличное от стандартного линейного пространства над полем Галуа.
В
работе изучается одна из абелевых подгрупп унитреугольной группы матриц ![]() порядка
порядка ![]() над полем Галуа
над полем Галуа ![]() , состоящем из
, состоящем из ![]() элементов. Указанная подгруппа содержит
элементы порядков
элементов. Указанная подгруппа содержит
элементы порядков ![]() , т.е. не является элементарной абелевой. Рассмотрены абелевы
группы кортежей
, т.е. не является элементарной абелевой. Рассмотрены абелевы
группы кортежей ![]() , операции над кортежами записываются нелинейными
равенствами. Определены различные линейные пространства на группах кортежей
, операции над кортежами записываются нелинейными
равенствами. Определены различные линейные пространства на группах кортежей ![]() над полем
над полем ![]() ,
, ![]() ,
, ![]() . Исследуемые группы полны, т.е. это группы с однозначным
извлечением корня.
. Исследуемые группы полны, т.е. это группы с однозначным
извлечением корня.
1. Абелева подгруппа группы унитреугольных матриц ![]()
Рассматривается
поле Галуа ![]() , состоящее из
, состоящее из ![]() элементов,
элементов, ![]() простое число, и группа унитреугольных матриц
простое число, и группа унитреугольных матриц ![]() ,
, ![]() , над полем
, над полем ![]() . В группе
. В группе ![]() выделяется подмножество
выделяется подмножество ![]() матриц, на диагоналях
которых находятся одинаковые элементы:
матриц, на диагоналях
которых находятся одинаковые элементы:
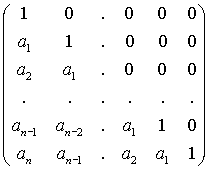 =
= ![]() .
.
Каждая
матрица однозначно определяется своим первым столбцом.
Лемма 1. Множество ![]() является абелевой подгруппой группы унитреугольных матриц
является абелевой подгруппой группы унитреугольных матриц ![]() .
.
# Единичная матрица ![]() есть
есть ![]() . Произведение матриц из
. Произведение матриц из ![]() является матрицей
того же вида:
является матрицей
того же вида:
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() . (1)
. (1)
Элементы обратной матрицы ![]() являются решением системы
линейных уравнений, получаемой по равенствам (1)
являются решением системы
линейных уравнений, получаемой по равенствам (1)
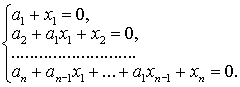
Система
уравнений имеет единственное решение, так как ее определитель отличен от 0. Это
означает, что ![]() вместе со всякой
матрицей содержит и ей обратную. Следовательно,
вместе со всякой
матрицей содержит и ей обратную. Следовательно, ![]() является подгруппой в
является подгруппой в
![]() . Равенства (1)
указывают на коммутативность умножения в
. Равенства (1)
указывают на коммутативность умножения в ![]() .#
.#
Для матриц ![]() из
из ![]() , где
, где ![]() кольцо целых чисел, в
работе [1; с. 160] установлено
равенство,
кольцо целых чисел, в
работе [1; с. 160] установлено
равенство, ![]() :
:
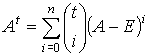 , (2)
, (2)
где 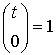 ,
, 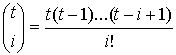 ;
;
которое
верно, в частности, для матриц из ![]() . В случае
. В случае ![]() имеем
имеем
![]() – нулевая матрица.
– нулевая матрица.
Равенство
(2) выполняется и для матриц из ![]() , как для элементов из
, как для элементов из ![]() . Важно установить, какие слагаемые содержатся в последнем элементе
первого столбца матрицы
. Важно установить, какие слагаемые содержатся в последнем элементе
первого столбца матрицы ![]() , если
, если ![]() . При
. При ![]() имеем:
имеем:
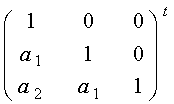 =
=![]() =
=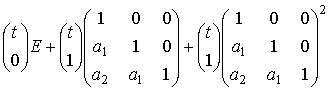
=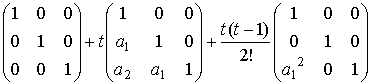 =
=
= 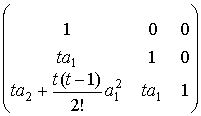 =
= ![]() .
.
Последнее
слагаемое в нижнем элементе первого столба матрицы ![]() при
при ![]() есть
есть ![]() . При
. При ![]() аналогичными
вычислениями находим:
аналогичными
вычислениями находим: ![]() =
= ![]() ,
,
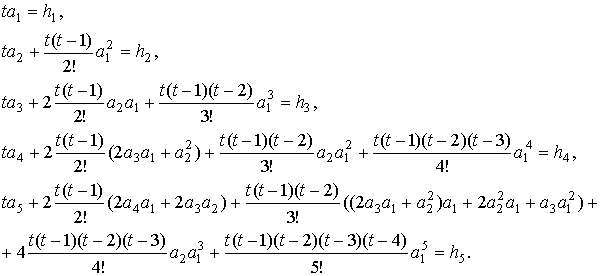
Если
![]() , то последнее слагаемое в нижнем элементе первого столбца матрицы
, то последнее слагаемое в нижнем элементе первого столбца матрицы
![]() равно
равно ![]() . Очевидно, в нижнем элементе первого столбца матрицы
. Очевидно, в нижнем элементе первого столбца матрицы ![]() последнее слагаемое
есть
последнее слагаемое
есть ![]() .
.
Матрица ![]() содержится в
содержится в ![]() .
.
2. Группы кортежей ![]() элементов поля
элементов поля ![]()
На конечнопорожденной нильпотентной
группе без кручения в книге [1; с. 159] введены целочисленные координаты.
Аналогично координаты вводятся в группах ![]() . Элементы групп записываются в виде кортежей из
. Элементы групп записываются в виде кортежей из ![]() и групповые операции
являются операциями над кортежами по аналогии с операциями над векторами. Групповая
операция в компонентах кортежей записывается нелинейно. Например, существует
биекция
и групповые операции
являются операциями над кортежами по аналогии с операциями над векторами. Групповая
операция в компонентах кортежей записывается нелинейно. Например, существует
биекция

![]() .
.
Произведению
матриц
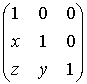
 =
=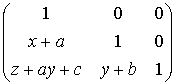
соответствует
сумма кортежей
![]() .
.
В
третьей компоненте суммы имеется слагаемое ![]() второго порядка, то
есть групповая операция на
второго порядка, то
есть групповая операция на ![]() нелинейна.
нелинейна.
Воспользуемся координатами на группах ![]() .
.
Теорема
1. Группа ![]() изоморфна группе кортежей
изоморфна группе кортежей ![]() с операцией
с операцией
![]() , (3)
, (3)
где компоненты суммы определяются
равенствами (1):
![]() ,
, ![]() ,
, ![]() .
.
# Биекция между элементами группы ![]() и кортежами из
и кортежами из ![]() такова:
такова:
![]() . (4)
. (4)
В
этой биекции матрице ![]() соответствует кортеж
соответствует кортеж ![]() , компоненты которого определяются равенствами (1). Из того,
что
, компоненты которого определяются равенствами (1). Из того,
что ![]() абелева группа, лемма
1, следует, что множество кортежей
абелева группа, лемма
1, следует, что множество кортежей ![]() с операцией (3)
является абелевой группой с операцией, определяемой равенствами (1) с
нелинейной операцией, определяемой равенствами. #
с операцией (3)
является абелевой группой с операцией, определяемой равенствами (1) с
нелинейной операцией, определяемой равенствами. #
Мы имеем группу кортежей ![]() . Нулевой элемент группы
. Нулевой элемент группы ![]() равен
равен ![]() =
= ![]() .
.
Известно, что множество кортежей ![]() является абелевой
группой относительно операции сложения
является абелевой
группой относительно операции сложения
![]() .
(5)
.
(5)
Это
группа ![]() . Операция (3) на множестве
. Операция (3) на множестве ![]() альтернативна
операции (5), поэтому она обозначена символом
альтернативна
операции (5), поэтому она обозначена символом ![]() . Альтернативная операция
. Альтернативная операция ![]() рассмотрена в работах
[2, 4], где изучается линейное пространство над полем
рассмотрена в работах
[2, 4], где изучается линейное пространство над полем ![]() действительных чисел с операциями
действительных чисел с операциями
![]() ,
, ![]() ,
, ![]() .
.
Это
линейное пространство использовано в построении альтернативной аффинной плоскости
![]() , [3]. Альтернативные операции нелинейны, компоненты
результатов операций, начиная со второй, содержат произведения компонент
исходных кортежей.
, [3]. Альтернативные операции нелинейны, компоненты
результатов операций, начиная со второй, содержат произведения компонент
исходных кортежей.
Для кортежей ![]() из
из ![]() определяются кратные
определяются кратные ![]() ,
, ![]() , с использованием степеней матриц из
, с использованием степеней матриц из ![]() , см. (2), или в
результате целочисленного повторения слагаемого
, см. (2), или в
результате целочисленного повторения слагаемого ![]() в суммировании
в суммировании ![]() , см. (1). Имеем следующую таблицу операций над кортежами из
, см. (1). Имеем следующую таблицу операций над кортежами из ![]() для начальных
значений
для начальных
значений ![]() .
.
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() =
= ![]() ,
,
![]() =
= ![]() ;
;
![]() ,
, ![]() =
=
![]() ,
,
![]() =
= ![]()
![]() ;
;
![]() ,
, ![]() =
=
![]() ,
,
![]() =
= ![]()
![]()
![]()
![]() .
.
При
![]() последнее слагаемое
последнее слагаемое ![]() ой компоненты кортежа
ой компоненты кортежа ![]()
![]() есть
есть ![]() .
.
Мы рассматриваем поле Галуа ![]() , состоящее из
, состоящее из ![]() элементов. Ниже установлено,
что в группе
элементов. Ниже установлено,
что в группе ![]() содержатся кортежи, порядки которых равны
содержатся кортежи, порядки которых равны ![]() . Пусть
. Пусть ![]() =
= ![]()
![]() . Найдем порядок
. Найдем порядок ![]() .
.
Теорема
2. Если ![]() есть поле, состоящее из
есть поле, состоящее из ![]() элементов, и
элементов, и ![]() , то
, то ![]() .
.
# Воспользуемся изоморфизмом групп ![]() и
и ![]() , см. теорему 1. В равенстве (2) положим
, см. теорему 1. В равенстве (2) положим ![]()
![]() ,
, ![]() . При
. При ![]() каждое число
каждое число 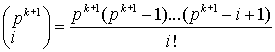 делится на
делится на ![]() , а значит сравнимо с нулем по модулю
, а значит сравнимо с нулем по модулю ![]() . Следовательно,
. Следовательно, ![]() . Вместе с тем
. Вместе с тем ![]() , так как
, так как 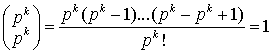 . Таким образом,
. Таким образом, ![]() . Значит, и
. Значит, и ![]() . #
. #
Доказанная теорема означает в
частности, что группа ![]() кортежей элементов
поля
кортежей элементов
поля ![]() , состоящего из
, состоящего из ![]() элементов, содержит
кортежи, порядки которых больше
элементов, содержит
кортежи, порядки которых больше ![]() . Группа
. Группа ![]() содержит элементы
порядка
содержит элементы
порядка ![]() , группа
, группа ![]() ,
, ![]() , содержит элементы порядка
, содержит элементы порядка ![]() .
.
3. Линейные пространства над полем Галуа
Рассматриваем поле Галуа ![]() , состоящее из
, состоящее из ![]() элементов, и
множество кортежей элементов поля
элементов, и
множество кортежей элементов поля ![]() . Если * есть операция сложения кортежей, то операцию
умножения кортежей на скаляры
. Если * есть операция сложения кортежей, то операцию
умножения кортежей на скаляры ![]() из поля
из поля ![]() обозначаем
обозначаем ![]() ; так как внешняя операция связана с внутренней. Имеется
линейное пространство
; так как внешняя операция связана с внутренней. Имеется
линейное пространство ![]() над полем
над полем ![]() :
: ![]() , где сложение есть (5) и операция
, где сложение есть (5) и операция ![]() такова
такова ![]() . Существуют и другие линейные пространства над другими
полями, носителем которых является множество кортежей
. Существуют и другие линейные пространства над другими
полями, носителем которых является множество кортежей ![]() , [5]. Выше, в п. 2, определена группа
, [5]. Выше, в п. 2, определена группа ![]() на носителе
на носителе ![]() с операцией (3),
альтернативной к (5). Воспользуемся внешней операцией
с операцией (3),
альтернативной к (5). Воспользуемся внешней операцией ![]() на
на ![]() . Она соответствует внешней операции (2) на
. Она соответствует внешней операции (2) на ![]() .
.
Лемма
2. В группе ![]() для всякой матрицы
для всякой матрицы ![]() и целого числа
и целого числа ![]() существует матрица
существует матрица ![]() , удовлетворяющая
равенству
, удовлетворяющая
равенству
![]() =
=![]() . (6)
. (6)
# На основе равенства (2) для величин ![]() получается система
уравнений, составленной по равенствам (1) с правыми частями
получается система
уравнений, составленной по равенствам (1) с правыми частями ![]() . Пример такой системы рассмотрен в п.1, составленной на
основе равенства
. Пример такой системы рассмотрен в п.1, составленной на
основе равенства ![]() =
= ![]() при
при ![]() . Нужно рассмотреть матрицу из
. Нужно рассмотреть матрицу из ![]() , заменить
, заменить ![]() на
на ![]() и
и ![]() на
на ![]() . Получаемая система уравнений имеет единственное решение. #
. Получаемая система уравнений имеет единственное решение. #
Лемма 2 означает, что справедлива
Теорема
3. ![]() является группой с однозначным извлечением корня, т.е. полной группой.
#
является группой с однозначным извлечением корня, т.е. полной группой.
#
Полнота группы
означает разрешимость уравнения (6) для всех ![]() и
и ![]() , см. [1; с. 86 – 90].
, см. [1; с. 86 – 90].
Ввиду изоморфизма групп ![]() и
и ![]() , группа кортежей
, группа кортежей ![]() обладает теми же
свойствами, что и группа матриц
обладает теми же
свойствами, что и группа матриц ![]() . На группе
. На группе ![]() имеется внешняя операция
имеется внешняя операция
![]() :
:
Определение.
Произведением кортежа ![]() на элемент
на элемент ![]() называется кортеж
называется кортеж ![]() , соответствующий матрице
, соответствующий матрице ![]() в изоморфизме (4).
в изоморфизме (4).
В п.2 приведены внешние операции на группах кортежей ![]() при
при ![]() . Лемма 2 определяет
кратное
. Лемма 2 определяет
кратное ![]() . Равенства (2) на основании изоморфизма (4) определяет
кратное
. Равенства (2) на основании изоморфизма (4) определяет
кратное ![]() =
= 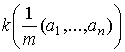 . Однако, конечного линейного пространства над полем
. Однако, конечного линейного пространства над полем ![]() рациональных чисел не
существует. Действительно, виду конечности линейного пространства, для кортежей
рациональных чисел не
существует. Действительно, виду конечности линейного пространства, для кортежей
![]() имеется число
имеется число ![]() , что
, что ![]() . Значит,
. Значит, ![]() сравнимо с нулем по
некоторому модулю и рациональное число
сравнимо с нулем по
некоторому модулю и рациональное число ![]() должно быть целым.
Таким образом, имеется пространство над конечным полем.
должно быть целым.
Таким образом, имеется пространство над конечным полем.
Пусть ![]() поле Галуа,
поле Галуа, ![]() .
.
Теорема
4. Структура ![]() , где
, где ![]() поле Галуа,
поле Галуа, ![]() ,
, ![]() наивысший порядок элементов из
наивысший порядок элементов из ![]() , является линейным
пространством, состоящем из кортежей из
, является линейным
пространством, состоящем из кортежей из ![]() с операцией сложения
с операцией сложения ![]() , см. (3), над кортежами,
и умножением
, см. (3), над кортежами,
и умножением ![]() кортежей на скаляры из поля
кортежей на скаляры из поля ![]() .
.
# По теореме 1, ![]() – абелева группа. На
кортежах
– абелева группа. На
кортежах ![]() из
из ![]() выше определены
кратные
выше определены
кратные ![]() ,
, ![]() . Согласно теореме 2, существует число
. Согласно теореме 2, существует число ![]() , что кортеж
, что кортеж ![]() из
из ![]() имеет порядок
имеет порядок ![]() . Рассматриваем поле
. Рассматриваем поле ![]() , изоморфное полю классов вычетов
, изоморфное полю классов вычетов ![]() по модулю
по модулю ![]() . Пусть
. Пусть ![]() принадлежит полной
системе вычетов из
принадлежит полной
системе вычетов из ![]() по модулю
по модулю ![]() . Умножение кортежей
. Умножение кортежей ![]() =
=![]() на скаляры из
на скаляры из ![]() есть умножение
кортежей на скаляры
есть умножение
кортежей на скаляры ![]() из указанной полной
системы вычетов; умножение происходит согласно определению, приведенному
выше. Выполняются свойства:
из указанной полной
системы вычетов; умножение происходит согласно определению, приведенному
выше. Выполняются свойства: ![]()
![]()
![]() =
= ![]() ;
; ![]() , так как справедливы соответствующие свойства для степеней
матриц из
, так как справедливы соответствующие свойства для степеней
матриц из ![]() . Аксиомы линейного
пространства для операций
. Аксиомы линейного
пространства для операций ![]() и
и ![]() выполняются. #
выполняются. #
4. Пример.
Пусть ![]() поле, состоящее из
двух элементов, т.е.
поле, состоящее из
двух элементов, т.е. ![]() . Имеем, что характеристика поля
. Имеем, что характеристика поля ![]() есть
есть ![]() . Таблицы операций в поле:
. Таблицы операций в поле:

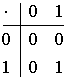
![]() есть группа матриц
есть группа матриц 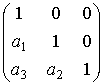 , где
, где ![]() , каждый из
, каждый из ![]() , является либо 0 либо 1. подгруппа
, является либо 0 либо 1. подгруппа ![]() состоит из матриц
состоит из матриц 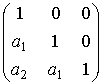 =
= ![]() . Обозначим:
. Обозначим: ![]() =
= 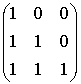 =
= ![]() . Находим степени
. Находим степени ![]() матрицы
матрицы ![]() , где
, где ![]() .
.
![]() =
= 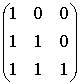
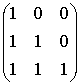 =
=  ,
,
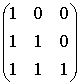
![]() =
= ![]()
![]() =
= 
 =
=  ,
,
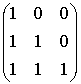
![]() =
= ![]()
![]() =
= 
 =
=  =
= ![]() , единичная матрица в группе
, единичная матрица в группе ![]() . Выполняется
. Выполняется ![]()
![]() при
при ![]() ,
, ![]() =
= ![]() . Очевидно, степени
. Очевидно, степени ![]() и
и ![]() совпадают, если
совпадают, если ![]() . Порядок матрицы
. Порядок матрицы ![]() из группы
из группы ![]() равен 4.
равен 4.
В биекции:
![]() ,
,
![]() является множеством
пар элементов поля
является множеством
пар элементов поля ![]() ; в биекции
; в биекции ![]() матрице
матрице ![]() =
= 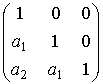 соответствует пара
соответствует пара ![]() . Находим:
. Находим:
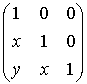
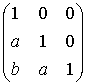 =
= 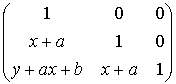 =
= 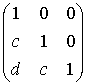 .
.
Произведению
матриц ![]() в биекции
в биекции ![]() соответствует пара
соответствует пара
![]() ,
,
где ![]() ,
, ![]() .
.
Тем
самым ![]() является изоморфизмом
между группами
является изоморфизмом
между группами ![]() и
и ![]() . Операция
. Операция ![]() сложения пар
альтернативна операции сложения
сложения пар
альтернативна операции сложения ![]() :
: ![]() в том смысле, что
операции
в том смысле, что
операции ![]() имеется альтернатива
имеется альтернатива ![]() . Возведению матриц
. Возведению матриц ![]() в целую степень
в целую степень ![]() соответствует в
автоморфизме
соответствует в
автоморфизме ![]() умножение пар из
умножение пар из ![]() на целое число:
на целое число:
![]() .
.
Умножение
пар на числа производится по правилу:
![]() ,
, ![]() .
.
Обозначим: ![]()
![]() . Степеням матрицы
. Степеням матрицы ![]() , выписанным выше, соответствуют пары, кратные
, выписанным выше, соответствуют пары, кратные ![]() .
.
![]() =
= ![]() ;
; ![]() =
= ![]() ;
;
![]() =
= ![]() =
= ![]() .
.
Таким
образом, ![]() при
при ![]() ,
, ![]() . Порядок элемента
. Порядок элемента ![]() группы
группы ![]() равен 4 =
равен 4 = ![]() , хотя пары из
, хотя пары из ![]() составлены из элементов поля
составлены из элементов поля
![]() . Группа
. Группа ![]() состоит из четырех
элементов
состоит из четырех
элементов ![]() и является
циклической, как и группа матриц
и является
циклической, как и группа матриц ![]() . Имеется линейное пространство
. Имеется линейное пространство ![]() над полем
над полем ![]() , поле
, поле ![]() состоит из четырех
элементов.
состоит из четырех
элементов.
Подводя
итоги, получаем следующее.
(а)
Существуют линейные пространства кортежей длины ![]() элементов поля Галуа,
состоящего из
элементов поля Галуа,
состоящего из ![]() элементов, над полем
элементов, над полем ![]() ,
, ![]() ,
, ![]() .
.
(б)
Линейные пространства ![]() и
и ![]() неизоморфны.
неизоморфны.
(в)
Не существует линейного пространства ![]() над полем
над полем ![]() .
.
(г)
Существует натуральное число ![]() такое, что порядок
кортежа
такое, что порядок
кортежа ![]() из
из ![]() превосходит любое
заданное число
превосходит любое
заданное число ![]() .
.
Последнее свойство линейных пространств
кортежей ![]() замечательно тем, что
имея поле, состоящее из
замечательно тем, что
имея поле, состоящее из ![]() элементов, можно
получить кортежи порядков
элементов, можно
получить кортежи порядков ![]() ,
, ![]() .
.
Литература.
1.
Каргаполов М.И.,
Мерзляков Ю.И. Основы теории групп. – М.: Наука, 1982. – 288с.
- Долгарев
А. И., Долгарев И.А. Альтернативное 2-мерное действительное линейное пространство.
Группа Ли замен базисов пространства. // Владикавказкий математический
журнал. – Владикавказ, 2008, Т.10, вып. 2. – С. 9 – 20.
- Долгарев
А.И., Долгарев И.А. Альтернативная аффинная плоскость.// Владикавказский
математический журнал – Владикавказ, 2007, Т.9, вып. 4. – С. 4 – 14.
4.
Долгарев А.И., Долгарев
И.А. Действительные линейные пространства малых размерностей с нелинейными
операциями. // Алгебра, логика и методика обучения математике. Материалы
Всероссийской конференции, посв. 100-летию со дня рожд. С.Л. Эдельмана.
Красноярск, 5-6 ноября 2010. Красноярск: КГПУ, С. 35 – 37.
5.
Долгарев И.А., Долгарев
А.И. Альтернативные действительные линейные пространства размерностей 2,3 и
4.// Известия высших учебных заведений. Поволжский регион.
Физико-математические науки. – 2011. № 1(17). – С. 3 – 19.