Математика/5. Математическое моделирование
Ефремов А.А.
Могилёвский
государственный областной институт
развития образования,
Беларусь
Моделирование итерационных процессов
с помощью функциональных уравнений
Под итерационным процессом в данной статье подразумевается
однозначно определённая последовательность повторяющихся операций. Природа
такого рода процессов достаточно многообразна, поэтому, с моей точки зрения,
неверно было бы сводить их лишь к процессам, связанным с теорией приближённых
вычислений.
Итерационные алгоритмы нашли наиболее широкое
применение в программировании. Так, любой цикл (одна из основных
алгоритмических структур) по сути представляет собой итерационный процесс.
В ходе моделирования циклических действий в
подавляющем большинстве случаев нельзя обойтись без применения ЭВМ, поскольку
обычно для этого требуется значительный объём арифметических расчётов. Однако в
основе работы алгоритма так или иначе лежит математический фундамент.
Таким образом, для глубокого понимания сути
итерационных процессов необходимо привлекать аппарат математического анализа, в
частности, теорию функциональных уравнений. Рассмотрим это на конкретном
примере.
Представим себе окружность, по периметру которой
расставлены натуральные числа от 1 до ![]() . На каждом шаге стирается (вычёркивается, удаляется) каждое
второе по ходу часовой стрелки число. Отсчёт начинается с 1. Так, на первом
шаге будут удалены все чётные числа. Ясно, что на каждом шаге количество чисел
на окружности уменьшается. Наступит момент, когда останется одно-единственное
число. Зададимся целью выяснить, какое число останется, например, при
. На каждом шаге стирается (вычёркивается, удаляется) каждое
второе по ходу часовой стрелки число. Отсчёт начинается с 1. Так, на первом
шаге будут удалены все чётные числа. Ясно, что на каждом шаге количество чисел
на окружности уменьшается. Наступит момент, когда останется одно-единственное
число. Зададимся целью выяснить, какое число останется, например, при ![]() .
.
Введём в рассмотрение функцию ![]() , которая представляет собой преобразование, совершаемое над
аргументом (в роли которого выступает окружность с числами). Результатом этого
преобразования является некоторое натуральное число. Таким образом,
, которая представляет собой преобразование, совершаемое над
аргументом (в роли которого выступает окружность с числами). Результатом этого
преобразования является некоторое натуральное число. Таким образом, ![]() .
.
Легко определить, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т.д.
и т.д.
Пользуясь методом математической индукции, можно
показать, что если ![]() , где
, где ![]() , то при последовательном вычёркивании каждого второго числа
последним останется число
, то при последовательном вычёркивании каждого второго числа
последним останется число ![]() . Однако этот способ, на мой взгляд, является слишком
«искусственным». Заметить эту закономерность отнюдь не просто.
. Однако этот способ, на мой взгляд, является слишком
«искусственным». Заметить эту закономерность отнюдь не просто.
Попробуем подойти к решению задачи несколько
иначе. Рассмотрим два случая.
1) ![]() . После первого шага получим ряд
. После первого шага получим ряд ![]() . Заметим, что если к каждому из оставшихся чисел прибавить
по единице и результат поделить пополам, будем иметь ряд
. Заметим, что если к каждому из оставшихся чисел прибавить
по единице и результат поделить пополам, будем иметь ряд ![]() . Следовательно, имеет место соотношение
. Следовательно, имеет место соотношение
![]() . (*)
. (*)
2) ![]() . После первой операции имеем последовательность
. После первой операции имеем последовательность ![]() . Если к каждому из этих чисел прибавить по единице и результат
поделить на два, получим ряд
. Если к каждому из этих чисел прибавить по единице и результат
поделить на два, получим ряд ![]() . Таким образом, можно записать
. Таким образом, можно записать
![]() . (**)
. (**)
Из (*) и (**) легко
найти, что весь процесс можно описать системой
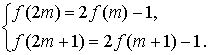
Применяя эти
рекуррентные соотношения, запишем
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Как было указано выше, ![]() . Выполняя вычисления значений функции
. Выполняя вычисления значений функции ![]() в обратном порядке,
получим, что
в обратном порядке,
получим, что ![]() .
.
Поставленную задачу
можно считать решённой. Для любого конечного ![]() описанный алгоритм
позволяет получить однозначный ответ.
описанный алгоритм
позволяет получить однозначный ответ.
Литература:
1. Блинков, А.Д. Московские математические регаты / Сост. А. Д. Блинков, Е. С. Горская, В.
М. Гуровиц. // М. : МЦНМО, 2007.
2. Роганов, Е.А. Рекурсия и итерация // Основы информатики и программирования: Учебное пособие.
— М. : МГИУ, 2001.