Математика / 5.Математическое моделирование

Димитриченко Д.П.

НИИ ПМА КБНЦ РАН, Россия, г. Нальчик

К вопросу о дифференцировании и интегрировании логических k-значных функций

В настоящей работе предложен способ дифференцирования логических функций, позволяющий проводить эффективный анализ дискретных функциональных зависимостей.

В работах [1,2] был предложен способ дифференцирования двоичных логических функций. В работе [3] предложена методика дифференцирования k-значных функций, использующая сложение по модулю k.

Пусть x переменная k-значной логики, где k - некоторое натуральное число, k >= 2.

Очевидно, что любое значение переменной x может быть получено при помощи выполнения конечного числа сложений единицы по модулю k.

Отметим на числовой прямой все возможные значения переменной x в порядке их возрастания.

Тогда, положив начальное значение x равное некоторому x*, и, последовательно прибавляя к x единицу (по правилам сложения по модулю k), мы вернемся в исходную точку x*, обойдя все точки в определенном направлении в сторону возрастания значений x.

Такое направление изменения значений переменной x мы назовем положительным.

Здесь и далее, + - это сложение по модулю k, а * - умножение по модулю k.

Множество элементов 0, 1, 2,… k-1 с введенными операциями + и * образуют кольцо (при простом k поле) с соответствующими свойствами [4].

Пусть теперь на множестве X: 0, … k-1 задана некоторая k-значная функция y=F(x): x принадлежит X. F: X → Y. Y, 0.. k-1.

И пусть F(x₁) = F₁, а F(x₂) = F₂.

Очевидно, что при переходе функции из точки x₁ в x₂ функция F(x) изменит свое значение на величину dF в положительном направлении своих значений такое, что: F(x1) +dF = F(x2).

Поскольку множество X с операцией + - сложение по модулю k является группой, то для любой пары значений функции F(x): F(x_i) = F_i и F(x_j) = F_j, где x_i и x_j некоторые значения аргументов функции F(x) величина dF будет определяться всегда, принимая значения 0, … , k-1.

Таким образом, мы можем говорить о приращении значения функции F(x) на величину dF при изменении аргумента x в положительном направлении.

Аналогом предельного перехода для дискретных функций будет рассмотрение приращения функции между двумя соседними (ближайшими в положительном направлении) точками.

Определение: Производной F′(x₀) функции F(x) в точке x₀ называется величина приращения функции при изменении значения аргумента x₀ на единицу в положительном направлении, такое что: F(x₀ +1) = F(x₀) + F′(x₀).

Исходя из определения производной, мы можем сформулировать теорему о существовании производной функции F в точке.

Теорема 1. Функция F(x) дифференцируема в точке x, если она определена в точках x = x+1.

Теорема 2. Всюду определенная функция F(x) дифференцируема во всех точках области определения.

Пусть F(x) и G(x), H(x) дифференцируемые в точке x функции, тогда выполнены следующие свойства:

Свойство 1. (F(x) +G(x))′ = F′(x) + G′(x), т.е. производная суммы равна сумме производных.

Свойство 2: Пусть C – произвольная константа, принимающая некоторое значение от 0 до k-1, тогда верно равенство: (CF(x))' = CF'(x), т.е. постоянную величину можно вынести за знак производной.

Свойство 3: Пусть F(x) и G(x) дифференцируемые в точке x функции. Тогда верно следующее равенство:

(F(x)G(x))' = F'(x)G(x) + F(x)G'(x) + F'(x)G'(x).

Свойство 3а: Производная произведения l дифференцируемых функций равна сумме произведений L членов, состоящих из всевозможных сочетаний функций и их производных.

Простейшее выражение получения значения функции в соседней точке x+1 через ее значение и значение ее производной в текущей точке x получается из определения производной: F(x+1) = F(x) + F'(x).

Таким образом, мы можем сформулировать следующую теорему:

Теорема 3. Пусть функция F(x) определена и дифференцируема до порядка k-1 включительно в точке x, тогда ее значение в точке x+k-1 выражается следующей формулой:

Для удобства, выражение, находящееся под знаком суммы обозначим через T(F,k-1) и будем называть полиномом Тейлора порядка k-1 относительно производных функции F.

Из способа вычисления коэффициентов для формулы Тейлора следует, что для ее построения можно воспользоваться мнемоническим правилом треугольника Паскаля, аналогичного тому, которое применяется для получения коэффициентов для бинома ньютона.

Особенность состоит в том, что здесь выполняются все сложения по модулю k.

Пусть на множестве значений x 0, 1, 2, …, k-1 определена функция F(x).

Пусть также выполняется следующее равенство: G'(x) = F(x).

Согласно формуле определения производной можно записать:

G(x₀) = c, где c – k-значная константа.

G(x₁) = c + F(x₀),

G(x₂) = c + F(x₀) + F(x₁),

G(x₃) = c + F(x₀) + F(x₁) + F(x₂),…,

G(x₀) = c + F(x₀) + … F(x_k-1).

Из единственности значения функции G(x) в точке x₀ следует тождество правых частей первого и последнего равенств, откуда вытекает необходимое требование к интегрируемой функции F(x):F(x₀) + F(x₁) + F(x₂) + … + F(x_k-1)=0.

Функцию, обладающую этим свойством будем называть функцией интегрируемой по контуру, так как значение следующее за x=k-1 будет x=0.

Свойство 1. Если функция F(x) интегрируема, то интегрируема функция F(x) + c, где с - произвольная k-значная константа.

Свойство 2. Если функция F(x) интегрируема, то интегрируема функция cF(x), где c - произвольная k-значная константа.

Свойство 3. Сумма интегрируемых функций также является интегрируемой функцией.

Рассмотрим частный случай полинома Тейлора, его дискретный аналог – полином Маклорена, разложение функции в точке x₀=0.

Учтя, что для всякого значения x=0,…,k-1 величины F(0), F’(0), F’’(0), …,F^(k-1)(0) будут оставаться неизменными, меняться будут сами коэффициенты при них.

Таким образом, коэффициенты при производных функции F(x) в точке x₀=0 можно считать специальными функциями I_j(x), где x,j=0,…,k-1, равные нулю, когда производные функции F(x) не участвуют при вычислении текущего значения функции F(x*).

Если теперь все коэффициенты всех k разложений функции F(x) выписать в виде некоторой матрицы T=t[x,j], где t[x,j] – значение соответствующего коэффициента для вычисления функции в точке x при производной порядка j;x,j=0,…, k-1, то каждому столбцу этой матрицы будет соответствовать определенная функция I_j(x).

Учтя, что:

1. Для любого x,j=0,…,k-1, t[x,j] = t[x-1,j] + t[x-1,j-1] по свойству построения полинома Тейлора;

2. Для любой функции F(x) самый левый столбец состоит из единиц, т.е. I₀(x)≡1.

3. Верхняя строка матрицы состоит из нулей за исключением элемента t[0,0] =1;

4. Каждый из столбцов может быть полностью вычислен, используя значения предыдущего (с меньшим номером) столбца, можно записать следующую формулу: 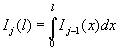, l,j=1,…,k-1, .

Таким образом, мы видим, что I_j(x) – это интегральные коэффициенты, каждый из которых получается интегрированием предыдущего коэффициента, как подинтегральной функции.

Теорема 5. Пусть функция F(x) определена в точке x₀=0 и имеет в ней производные до порядка k-1 включительно, тогда она представима в виде следующего интегрального разложения: .

Следствие. Для получения производной функции f(x), представленной виде интегрального разложения необходимо продифференцировать интегральные коэффициенты: .

Пусть G(x) – первообразная функции F(x), тогда можно сформулировать следующую теорему.

Теорема 6. Пусть функция F(x) определена в точке x₀=0 вместе со своими производными до порядка k-2 включительно, тогда , где c- значение первообразной G(x) в точке x=0.

Литература

1. Горбатов В.А. Фундаментальные основы дискретной математики.- М.: Наука, 2000.- 544 с.

2. Шевелев Ю.П. Дискретная математика.- Томск.: 2003.- 118 с.

3. Пантелеев В.И. Полиномиальное разложение k-значных функций по операторам Дифференцирования и нормализации // Известия высших учебных заведений: Математика №1, 1998. С. 82-103.

4. Кострыкин А.И. Введение в алгебру.- М.: Наука, 1977.- 320 с.