ON THE DIMENSION OF
THE SPACE IN THE EARLY UNIVERSE
V.V.Skobelev
Moscow State Industrial University; E-mail:
v.skobelev@inbox.ru
Abstract. It is shown
that if we consider fermions (quarks, electrons) generated by superstrings in
the early Universe a degenerate ideal quantum gas, the entropy of the system
has a local maxima in spaces with a number of dimensions equal to ![]()
![]() Thus, there is reason
to believe that the Universe was formed in the space with just such a number of
dimensions. An argument in favor of the dominance of space
Thus, there is reason
to believe that the Universe was formed in the space with just such a number of
dimensions. An argument in favor of the dominance of space ![]() is brought. With
further evolution, if we continue to adhere to the fundamental principle of the
second law of thermodynamics, due to changes in temperature and composition,
the space
is brought. With
further evolution, if we continue to adhere to the fundamental principle of the
second law of thermodynamics, due to changes in temperature and composition,
the space![]() apparently started to match the maximum entropy.
apparently started to match the maximum entropy.
I. INTRODUCTION
The modern theories do not exclude the possibility of the existence of
spaces with the number of dimensions more than![]() , some of which might be hidden from us. For example, in the
popular theory of superstrings the dimension of the space
, some of which might be hidden from us. For example, in the
popular theory of superstrings the dimension of the space ![]()
![]() [1,2]is possible,
while the number of dimensions of our space is three. In the present article we
attempt to clarify the issue in relation to the first instants of the Universe
(about 0.01s from the "start") when, apparently, the question of the
dimension of the space in which it could continue to evolve, was “being
solved”. We assume that in these first moments of the Universe it was governed
by the laws of quantum mechanics, while the majority of other laws of physics
had not yet "joined", partially because it was not an ordinary
matter, but there were only superstrings primarily in their excited states,
quarks and electrons. The second law of thermodynamics, according to which the
most probable states get implemented, has to deal not only with physical but
with mathematical laws, and we further assume that in this era the Universe has
evolved in accordance with the fundamental law of nature. In this regard, the
fermion excitations of superstrings form in the space with the highest entropy
level. That is why the problem of computing of the entropy
[1,2]is possible,
while the number of dimensions of our space is three. In the present article we
attempt to clarify the issue in relation to the first instants of the Universe
(about 0.01s from the "start") when, apparently, the question of the
dimension of the space in which it could continue to evolve, was “being
solved”. We assume that in these first moments of the Universe it was governed
by the laws of quantum mechanics, while the majority of other laws of physics
had not yet "joined", partially because it was not an ordinary
matter, but there were only superstrings primarily in their excited states,
quarks and electrons. The second law of thermodynamics, according to which the
most probable states get implemented, has to deal not only with physical but
with mathematical laws, and we further assume that in this era the Universe has
evolved in accordance with the fundamental law of nature. In this regard, the
fermion excitations of superstrings form in the space with the highest entropy
level. That is why the problem of computing of the entropy![]() of any of the fermion components as a function of space
dimension
of any of the fermion components as a function of space
dimension![]() rises. For simplicity, we assume that the system of fermions
is a degenerate Fermi gas. There are good reasons to do that: because of the
high concentration of fermions in an initially small volume of the Universe of
their kinetic energy at the Fermi level could considerably exceed the
temperature value. Note that the hypothesis of an extremely high temperature of
the early Universe at the stage of the Big Bang [2] relates, as we believe, to
a later point when the number of particles reaching the point at which we have
the usual statistical description of a system with temperature as a parameter
of its condition, and the second law of thermodynamics was an absolute exact
law of nature. If the number of fermions is limited and does not reach the
point at which the probability of states with maximum entropy is practically
equal to unity, the second law of thermodynamics indicates only a preferred
direction of evolution of the system with the realization of such states, and
the parameter
rises. For simplicity, we assume that the system of fermions
is a degenerate Fermi gas. There are good reasons to do that: because of the
high concentration of fermions in an initially small volume of the Universe of
their kinetic energy at the Fermi level could considerably exceed the
temperature value. Note that the hypothesis of an extremely high temperature of
the early Universe at the stage of the Big Bang [2] relates, as we believe, to
a later point when the number of particles reaching the point at which we have
the usual statistical description of a system with temperature as a parameter
of its condition, and the second law of thermodynamics was an absolute exact
law of nature. If the number of fermions is limited and does not reach the
point at which the probability of states with maximum entropy is practically
equal to unity, the second law of thermodynamics indicates only a preferred
direction of evolution of the system with the realization of such states, and
the parameter ![]() in the Fermi-Dirac
distribution is not the temperature in the conventional sense, and approval of
an extremely large value of the deficit of the particles immediately after the
start of their generation by superstrings does not make sense. However, we
further refer to this parameter as to the temperature for major
simplicity.
in the Fermi-Dirac
distribution is not the temperature in the conventional sense, and approval of
an extremely large value of the deficit of the particles immediately after the
start of their generation by superstrings does not make sense. However, we
further refer to this parameter as to the temperature for major
simplicity.
II. ENTROPY OF THE FERMION GAS IN ![]() - DIMENSION SPACE
- DIMENSION SPACE
The total
number of fermions in space of ![]() dimensions is
determined by the basic formula of Fermi-Dirac statistics:
dimensions is
determined by the basic formula of Fermi-Dirac statistics:
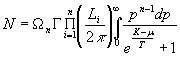 , (1)
, (1)
Where![]() is the statistical weight of state with a given value of the
relativistic kinetic energy
is the statistical weight of state with a given value of the
relativistic kinetic energy![]() , which we further consider independent from
, which we further consider independent from![]() ,
, ![]() - the chemical
potential,
- the chemical
potential, ![]() - normalization lengths of the axes,
- normalization lengths of the axes, ![]() - total angle in the space of
- total angle in the space of ![]() dimensions which can be expressed in terms of
dimensions which can be expressed in terms of ![]() - function [3]:
- function [3]:
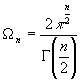 . (2)
. (2)
Determining
the concentration in the space of ![]() dimensions by
equation
dimensions by
equation
![]() , (3)
, (3)
we get:
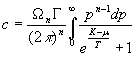 . (4)
. (4)
In
the case of a completely degenerate Fermi gas ![]() we find:
we find:
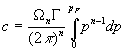 ,
(5)
,
(5)
Where ![]() is the Fermi
momentum, for which we therefore have:
is the Fermi
momentum, for which we therefore have:
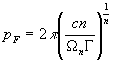 . (6)
. (6)
In
accordance with the ordinary differential equation for ![]() - potential [4]
- potential [4]
![]() (7)
(7)
the entropy can be found from its known
value:
![]() . (8)
. (8)
In our
case, the ![]() -potential per unit
"volume" is equal to
-potential per unit
"volume" is equal to
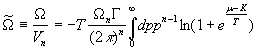 . (9)
. (9)
Integration
by parts gives:
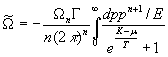 ,
,![]() ,
,
and with
the change of variable ![]() we obtain:
we obtain:
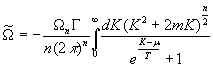 . (10)
. (10)
Furthermore,
we use the asymptotic expansion of the integral form (10) with respect to
temperature [4] in the case of a degenerate Fermi gas, which we put down in a
generalized form as follows:
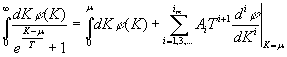 . (11)
. (11)
Note that
the contribution to (8) gives only the second term in (11) with explicit
dependence on temperature, since the derivative (8) is taken at a constant![]() , and the dependence
, and the dependence ![]() upon differentiation should not be considered. The index of
summation in (11) takes odd values (see also [4]) with maximum
upon differentiation should not be considered. The index of
summation in (11) takes odd values (see also [4]) with maximum![]() , and the way of determining of it at concrete
, and the way of determining of it at concrete ![]() will be indicated lower, and the coefficient
will be indicated lower, and the coefficient ![]() equal to:
equal to:
![]() , (12)
, (12)
where ![]() is the Riemann
function in area
is the Riemann
function in area ![]() is defined by equation [5]:
is defined by equation [5]:
![]() .
.
After the
transition to dimensionless variables we write the contribution we’re
interested in ![]() in the form
in the form
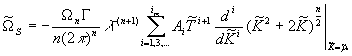 . (13)
. (13)
Here, ![]()
![]() ,
,![]() . For the further, we also give the expression of
the dimensionless momentum at the Fermi level
. For the further, we also give the expression of
the dimensionless momentum at the Fermi level![]() , which, according to (6), is equal to
, which, according to (6), is equal to
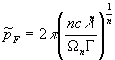 =
=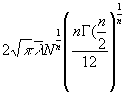 , (14)
, (14)
where we
used the formula (2), and the expression is written for the quarks (![]() ). For
simplicity we also believe that our system is in the
). For
simplicity we also believe that our system is in the ![]() -dimensional cube with side
-dimensional cube with side![]() . Since the cube in a
. Since the cube in a ![]() -dimensional space is
obtained by designing a cube in
-dimensional space is
obtained by designing a cube in ![]() -dimensional space on its face, then at the dimension change of
the space
-dimensional space on its face, then at the dimension change of
the space![]() , as also
, as also ![]() should be regarded
as constant; in this connection in (14) the notation
should be regarded
as constant; in this connection in (14) the notation ![]() is introduced (in the same
time,
is introduced (in the same
time, ![]() ).
Obviously,
).
Obviously, ![]() should be perceived as effective size of the early Universe.
As will be seen, a non-relativistic case is realized in it:
should be perceived as effective size of the early Universe.
As will be seen, a non-relativistic case is realized in it:
![]()
![]() , (15)
, (15)
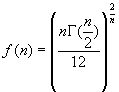 . (15a)
. (15a)
Inequality
(15) can always be observed for an appropriate choice of "free"
parameter![]() . Performing the (15), only the last term in parentheses
(13) makes the contribution. Next, we consider the values of the
derivative in various cases:
. Performing the (15), only the last term in parentheses
(13) makes the contribution. Next, we consider the values of the
derivative in various cases:
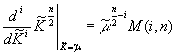 ,
(16)
,
(16)
1)![]() even,
even,![]()
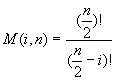 , (16a)
, (16a)
2)![]() even,
even,![]()
![]() ,
(16b)
,
(16b)
3)![]() odd,
odd,![]()
![]() , (16c)
, (16c)
4)![]() odd,
odd,![]() ,
, ![]() , (16d)
, (16d)
The
expression (16d) is the key for the purposes of this article. Combining
expressions (8), (12) - (16), we find the total entropy of the degenerate
non-relativistic quarks system, which in our units is a dimensionless quantity:
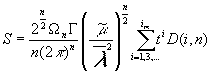 ,
, ![]() (17)
(17)
![]() . (17a)
. (17a)
Note that these expressions are valid when
the non-relativistic condition (15) and the corresponding limits on the
temperature![]() , which in view of (15a)) can be written in a
more convenient form as a condition on possible values of parameters
, which in view of (15a)) can be written in a
more convenient form as a condition on possible values of parameters ![]() :
:
![]() (17b)
(17b)
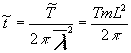 . (17c)
. (17c)
It is
possible to check that the expression (17)
at![]() with
the "replacement" of the quarks for electrons
with
the "replacement" of the quarks for electrons ![]() and values
and values ![]() coincide with the corresponding formula of the book [4], in
which, as in most other studies, only the linear term of the expansion of
entropy with respect to temperature was considered.
coincide with the corresponding formula of the book [4], in
which, as in most other studies, only the linear term of the expansion of
entropy with respect to temperature was considered.
In the
ultrarelativistic case
![]() , (18)
, (18)
when the first summand in parentheses in (13)
dominates, we obtain:
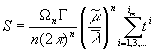
![]() ,
(19)
,
(19)
![]() , (19à)
, (19à)
with the
temperature limitation![]() , having form
, having form
![]() ,
(19b)
,
(19b)
![]() .
(19c)
.
(19c)
In the
formula (19) ![]() , if
, if ![]() is even, and
is even, and![]() , if
, if ![]() is odd. As seen from
(19), there is no fundamental difference between "odd"
is odd. As seen from
(19), there is no fundamental difference between "odd" ![]() and "even"
and "even" ![]() spaces in the sense of presence of maxima and minima of the
entropy in the ultrarelativistic case (the entropy increases monotonically with
increasing of
spaces in the sense of presence of maxima and minima of the
entropy in the ultrarelativistic case (the entropy increases monotonically with
increasing of![]() ), which can be determined also by a specific calculation,
taking for example, neglecting the temperature dependence of the chemical
potential
), which can be determined also by a specific calculation,
taking for example, neglecting the temperature dependence of the chemical
potential![]() . Likewise, a) the calculation of the degeneracy temperature
. Likewise, a) the calculation of the degeneracy temperature ![]() and entropy of the degenerate boson gas in
and entropy of the degenerate boson gas in ![]() -dimensional space, and b) the entropy of photon gas, lead to
the same conclusion about the monotonic variation of entropy. The results
obtained by standard methods [4] are as follows:
-dimensional space, and b) the entropy of photon gas, lead to
the same conclusion about the monotonic variation of entropy. The results
obtained by standard methods [4] are as follows:
a)
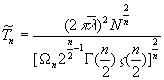 , (20a)
, (20a)
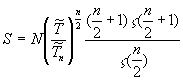 ,
(20b)
,
(20b)
b)
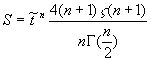 , (21)
, (21)
where the
value![]() is given by formula (19c).
is given by formula (19c).
III. DISCUSSION
Note that
the role of "primary" bosons in the early Universe, could be claimed
by axions, "responsible" for the CP-invariance of strong interactions
[6], and having a small mass ![]() [7,8], and also by
Higgs bosons [9], by which the Standard Model particles acquire mass. In this
case the bosons can also be viewed as excited states of superstrings [2]. But,
as already noted, neither they nor the photons “chose” the space with given
values of invariants
[7,8], and also by
Higgs bosons [9], by which the Standard Model particles acquire mass. In this
case the bosons can also be viewed as excited states of superstrings [2]. But,
as already noted, neither they nor the photons “chose” the space with given
values of invariants![]() in which the early Universe existed. The situation is
completely different, taking into account the entire temperature range (11) in
the case of non-relativistic fermion gas, the entropy value if which is given
by (16), (17). That is, at even
in which the early Universe existed. The situation is
completely different, taking into account the entire temperature range (11) in
the case of non-relativistic fermion gas, the entropy value if which is given
by (16), (17). That is, at even![]() , according to (16a, b), series (17) is cut off
"automatically" on
, according to (16a, b), series (17) is cut off
"automatically" on![]() , if
, if ![]() is even, and
is even, and ![]() if
if ![]() is odd. At the odd
is odd. At the odd ![]() the number (17) by a
factor
the number (17) by a
factor ![]() !! in (16d) diverges generally because, in
general, the decomposition (11) used is asymptotic and not convergent [7]. The
number must be torn off "by force" from physical considerations. Here
are the relevant arguments. From (16d) it is seen that in the spaces
!! in (16d) diverges generally because, in
general, the decomposition (11) used is asymptotic and not convergent [7]. The
number must be torn off "by force" from physical considerations. Here
are the relevant arguments. From (16d) it is seen that in the spaces ![]() at the values
at the values ![]()
![]() the contribution to the sum (17) is positive, as at
the contribution to the sum (17) is positive, as at ![]() , thereby increasing its value, and in the spaces
, thereby increasing its value, and in the spaces ![]() it is negative,
reducing the value of the sum at
it is negative,
reducing the value of the sum at![]() . This means that in the spaces
. This means that in the spaces ![]() there will be maximum
entropy, and in the spaces
there will be maximum
entropy, and in the spaces ![]() there will be minimum
entropy. Further, because of the factor
there will be minimum
entropy. Further, because of the factor ![]() in (16c, d) the peaks
will indefinitely increase with increasing of
in (16c, d) the peaks
will indefinitely increase with increasing of ![]() , as in the above-mentioned
cases of boson and ultrarelativistic fermion gases, which is unacceptable from
physical considerations. Thus, there should be such a maximum value
, as in the above-mentioned
cases of boson and ultrarelativistic fermion gases, which is unacceptable from
physical considerations. Thus, there should be such a maximum value ![]() that at
that at ![]() the second law of
thermodynamics in the terms we use is not applicable. Further, in the space
the second law of
thermodynamics in the terms we use is not applicable. Further, in the space ![]() because of the same factor
because of the same factor ![]() the negative entropy
will be achieved at the lowest value of the index of summation
the negative entropy
will be achieved at the lowest value of the index of summation ![]() rather than in spaces
such as
rather than in spaces
such as ![]() with a lower value
with a lower value![]() . To make entropy remain positive in these spaces, the number
(17) in them should be cut at
. To make entropy remain positive in these spaces, the number
(17) in them should be cut at![]() . As far as at the same parameters
. As far as at the same parameters ![]() the values of
the entropy in the spaces
the values of
the entropy in the spaces ![]() are not actually
independent, the temperature series (17) in the spaces
are not actually
independent, the temperature series (17) in the spaces ![]() should be truncated
at the same value
should be truncated
at the same value![]() .
.
In fact,
let us put down the equation of the form (17) ![]() for the two types of "odd spaces":
for the two types of "odd spaces":
![]() , (22a)
, (22a)
![]() . (22b)
. (22b)
With the
first equation we can find function![]() ; substituting
it in (22b), and then we have:
; substituting
it in (22b), and then we have:
![]() . (23)
. (23)
Since the
function![]() is defined up to
is defined up to ![]() inclusively, the
expansion
inclusively, the
expansion ![]() in series by
in series by ![]() should be done with
the same precision as required. Only the value of local maxima in the spaces
should be done with
the same precision as required. Only the value of local maxima in the spaces ![]() depends on the way of
"breaking" the series (17)
while they stay themselves, allocating these spaces among others.
depends on the way of
"breaking" the series (17)
while they stay themselves, allocating these spaces among others.
Thus,
although we do not have a clear recipe of definition ![]() (perhaps this value
can be determined from the condition of small fluctuations of the entropy
(perhaps this value
can be determined from the condition of small fluctuations of the entropy![]() , we are studying this issue), it is clear from the foregoing
that the graph of dependence of the entropy
, we are studying this issue), it is clear from the foregoing
that the graph of dependence of the entropy![]() on
on ![]() for the
non-relativistic degenerate fermion gas should be a broken line with local
maxima at
for the
non-relativistic degenerate fermion gas should be a broken line with local
maxima at ![]() and with minima at
and with minima at ![]() which must be
constructed also considering the approximate constraints (17b) on the
temperature.
which must be
constructed also considering the approximate constraints (17b) on the
temperature.
From
the steps of the calculations we have done,
another conclusion can be made. As seen, the inequality (17b) permits a
wider range of parameter values in the area ![]() ,
, ![]() at the lowest value
at the lowest value![]()
![]() , i.e. at
, i.e. at ![]() . Since the expansion of the range is actually equivalent to
increasing of the statistical weight of the quarks in this space, then above
all the spaces of the type
. Since the expansion of the range is actually equivalent to
increasing of the statistical weight of the quarks in this space, then above
all the spaces of the type ![]() it is considered most
likely that the early Universe could get in space
it is considered most
likely that the early Universe could get in space ![]() (which is consistent
with the concept of five-dimensional cosmological string model [10]), which
partially explains its transition due to changes in temperature and composition
in the "neighbor" odd space
(which is consistent
with the concept of five-dimensional cosmological string model [10]), which
partially explains its transition due to changes in temperature and composition
in the "neighbor" odd space![]() , to which the maximum entropy related in future.
, to which the maximum entropy related in future.
REFERENCES:
1. Veneziano G., Nuovo
Cim. V.57A, P.190, 1968.
2. Greene Brian, The
Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the
Ultimate Theory, Vintage Series, Random House Inc.,2000.
3. N. Ya. Vilenkin, Special functions and the theory of groups
representations, (in Russian), Ìoscow, Nauka, 1965.
4. L.D. Landau and E.M. Lifshitz, Course of Theoretical Physics,
Vol.5: Statistical Physics: Part 1, Butterworth-Heinemann, Oxford, 2000.
5. I.S. Gradshteyn and I.M. Ryzhik, Tables of Integrals, Sums, Series, and Products,
Acad. Press, New York, 1980.
6. R.D. Peccei and H.R, Quinn, Phys. Rev. Lett.,V.38, P.1440,
1977; Phys. Rev. V. D16, P. 179,1977.
7. J.E. Kim, Phys. Rep., V.150, P.1,1987.
8. H.Y. Cheng, Phys. Rep., V. 158,P.1, 1988.
9. P.W. Higgs, Phys. Lett., V.12,P.132,1964.
10. G.C. Samanta, S. Debata ,
J. Mod. Phys., V. 3, P. 180, 2012.