Способы
решения систем логических уравнений
Киргизова
Е.В., Немкова А.Е.
Лесосибирский
педагогический институт –
филиал
Сибирского федерального университета, Россия
Умение мыслить последовательно, рассуждать
доказательно, строить гипотезы, опровергать негативные выводы, не приходит само
по себе, это умение развивает наука логика [1]. Логика – это наука, изучающая
методы установления истинности или
ложности одних высказываний на основе истинности или ложности других
высказываний [1].
Овладение азами этой науки невозможно без
решения логических задач. Проверка сформированности умений применять свои
знания в новой ситуации осуществляется за счет сдачи. В частности, это умение
решать логические задачи. Задания В15 в ЕГЭ, являются заданиями повышенной
сложности, так как они содержат системы логических уравнений. Можно выделить
различные способы решения систем логических уравнений. Это сведение к одному
уравнению, построение таблицы истинности, декомпозиция, последовательное
решение уравнений и т.д.
Задача: Решить систему
логических уравнений:
Рассмотрим метод сведения к одному уравнению.
Данный метод предполагает преобразование логических уравнений, таким образом,
чтобы правые их части были равны истинностному значению (то есть 1). Для этого
применяют операцию логического отрицания. Затем, если в уравнениях есть сложные
логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом
объединяем уравнения в одно, равносильное системе, с помощью логической
операции «И». После этого, следует сделать преобразования полученного уравнения
на основе законов алгебры логики и получить конкретное решение системы.
Решение 1: Применяем
инверсию к обеим частям первого уравнения:
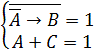
Представим импликацию через базовые
операции «ИЛИ», «НЕ»:
Поскольку левые части уравнений
равны 1, можно объединить их с помощью операции “И” в одно уравнение,
равносильное исходной системе:
Раскрываем
первую скобку по закону де Моргана и преобразовываем полученный результат:
Полученное
уравнение, имеет одно решение: A=0, B=0 и C=1.
Следующий способ – построение таблиц истинности.
Поскольку логические величины имеют только два значения, можно просто перебрать
все варианты и найти среди них те, при которых выполняется данная система
уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений
системы и находим строку с нужными значениями.
Решение 2:
Составим таблицу истинности для системы:
|
A |
B |
C |
|
|
|
|
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
Полужирным выделена строчка, для
которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.
Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из
переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения.
Затем можно зафиксировать значение второй переменной и т.д.
Решение 3: Пусть A = 0, тогда:
Из первого уравнения получаем B=0,
а из второго – С=1. Решение системы: A =
0, B = 0 и C = 1.
Так же можно воспользоваться
методом последовательного решения уравнений, на каждом шаге добавляя по
одной переменной в рассматриваемый набор. Для этого необходимо преобразовать
уравнения таким образом, что бы переменные вводились в алфавитном порядке.
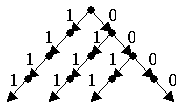
Далее строим дерево решений, последовательно добавляя в него переменные.
Первое уравнение системы зависит
только от A и B, а второе уравнение от А и C. Переменная А может принимать 2
значения 0 и 1:
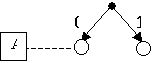
Из первого уравнения следует, что 
, поэтому при A =
0 получаем B = 0, а при A = 1 имеем B = 1. Итак, первое
уравнение имеет два решения относительно переменных A и B.
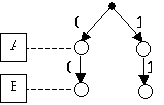
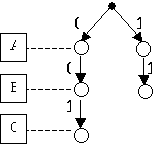Изобразим второе уравнение, из которого определим значения C для каждого варианта. При A=1 импликация не может быть ложной, то есть вторая ветка дерева не
имеет решения. При A=0 получаем единственное решение C = 1:
Таким
образом, получили решение системы: A =
0, B = 0 и C = 1.
В ЕГЭ по информатике очень часто требуется
определить количество решений системы логических уравнений, без нахождения
самих решений, для этого тоже существуют определенные методы. Основной способ
нахождения количества решений системы логических уравнений – замена переменных. Сначала необходимо
максимально упростить каждое из уравнений на основе законов алгебры логики, а
затем заменить сложные части уравнений новыми переменными и определить
количество решений новой системы. Далее вернуться к замене и определить для нее
количество решений.
Задача: Сколько решений имеет уравнение (A→B) +
(C→D) = 1? Где A, B, C, D –
логические переменные.
Решение: Введем новые переменные:
X = A→B и Y = C→D. С
учетом новых переменных уравнение запишется в виде: X + Y =
1.
Дизъюнкция верна в трех случаях: (0;1), (1;0) и
(1;1), при этом X и Y является импликацией,
то есть является истинной в трех случаях и ложной – в одном. Поэтому случай
(0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1)
– будет соответствовать девяти возможным сочетаниям параметров исходного
уравнения. Значит, всего возможных решений данного уравнения 3+9=15.
Следующий способ определения количества решений
системы логических уравнений – бинарное
дерево. Рассмотрим данный метод на примере.
Задача: Сколько различных
решений имеет система логических уравнений:
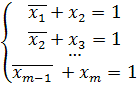
Приведенная система уравнений равносильна
уравнению:
(x1 → x2)*( x2 → x3)*…*( xm-1 → xm) = 1.
Предположим, что x1 –
истинно, тогда из первого уравнения получаем, что x2 также истинно, из
второго - x3=1, и так далее до xm = 1. Значит набор (1; 1; …; 1) из m
единиц является решением системы. Пусть теперь x1=0, тогда из первого
уравнения имеем x2 =0 или x2 =1.
Когда x2 истинно получаем, что
остальные переменные также истинны, то есть набор (0; 1; …; 1) является
решением системы. При x2=0 получаем, что x3=0 или x3=, и так далее.
Продолжая до последней переменной, получаем, что решениями уравнения являются
следующие наборы переменных (m+1 решение, в каждом
решении по m значений переменных):
(1; 1; 1; …; 1)
(0; 1; 1; …; 1)
…
(0; 0; 0; …; 0)
Такой подход хорошо иллюстрируется с помощью
построения бинарного дерева. Количество возможных решений – количество
различных ветвей построенного дерева. Легко заметить, что оно равно m+1.
|
Переменные |
Дерево |
Количество
решений |
|
x1 |
|
|
|
x2 |
3 |
|
|
x3 |
4 |
|
|
… |
… |
В случае трудностей в рассуждениях и построении
дерева решений можно искать решение с использованием таблиц истинности, для одного – двух уравнений.
Перепишем систему уравнений в виде:
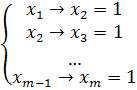
И составим таблицу истинности отдельно для
одного уравнения:
|
x1 |
x2 |
(x1 → x2) |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Составим таблицу истинности для двух уравнений:
|
x1 |
x2 |
x3 |
x1 → x2 |
x2 → x3 |
(x1 → x2) * (x2 → x3) |
|
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
Далее можно увидеть, что одно уравнение истинно
в следующих трех случаях: (0; 0), (0; 1), (1; 1). Система двух уравнений истина
в четырех случаях (0; 0; 0), (0; 0; 1), (0; 1; 1), (1; 1; 1). При этом сразу
видно, что существует решение, состоящее из одних нулей и еще m решений,
в которых добавляется по одной единице, начиная с последней позиции до
заполнения всех возможных мест. Можно предположить, что общее решение будет
иметь такой же вид, но чтобы такой подход стал решением, требуется
доказательство, что предположение верно.
Подводя итог всему вышесказанному, хочется
обратить внимание, на то, что не все рассмотренные методы являются
универсальными. При решении каждой системы логических уравнений следует
учитывать ее особенности, на основе которых и выбирать метод решения.
Литература:
1. Логические задачи / О.Б.
Богомолова – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2006. – 271 с.: ил.
2. Поляков К.Ю. Системы
логических уравнений / Учебно-методическая газета для учителей информатики:
Информатика №14, 2011 г.