Физика/ 1. Теоретическая физика./ Теоретическая механика.
К. физ.-мат.
наук Севрюков П.Ф.
Ставропольский
государственный педагогический институт, Россия.
Введение канонических переменных «действие-угол»
в возмущённой задаче Баррара.
Рассмотрим движение спутника,
принимаемого за материальную точку, в поле тяготения осесимметричной планеты.
Если ось аппликат направить вдоль ось динамической симметрии планеты, а начало
координат поместить в произвольной точке этой оси, то гравитационный потенциал
в стандартных обозначениях будет иметь вид
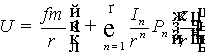 , (1)
, (1)
где f – гравитационная постоянная, т – масса планеты, r – модуль
радиус-вектора, In – постоянный
параметр, Рn – полином Лежандра n
– го порядка.
Гравитационное поле планеты будем
аппроксимировать полем тяготения Баррара [1, 2]. При этом начало координат
поместим в шаровую точку инерции планеты, тогда I1=с. Это значение составляет аппликату
центра масс планеты, I2=0, а
потенциал Баррара запишется следующим образом:
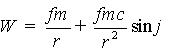 , (2)
, (2)
где sinφ=![]() . Оставшиеся
члены гравитационного потенциала составят пертурбационную функцию
. Оставшиеся
члены гравитационного потенциала составят пертурбационную функцию
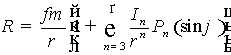 , (3)
, (3)
U=W+R. (4)
Задача Баррара
полностью учитывает возмущающий эффект второй зональной гармоники
гравитационного потенциала планеты. Уравнение движения невозмущённой задачи
Баррара интегрируется в замкнутом виде в квадратурах. [2]
В сферических
координатах r, φ, λ решение невозмущённой задачи Баррара имеет вид
![]() (5)
(5)
![]() (6)
(6)
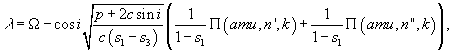 (7)
(7)
где
![]() , (8)
, (8)
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() , (12)
, (12)
![]() . (13)
. (13)
![]() - неполные
эллиптические интегралы III рода, модуль
и параметры которых равны
- неполные
эллиптические интегралы III рода, модуль
и параметры которых равны
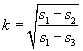 ,
, ![]() ,
, ![]() .
.
В формулах (5)-(13) а, e, i, Ω, v, ω являются аналогами большой
полуоси, эксцентриситете, наклона орбиты, долготы восходящего узла, истинной
аномалии и аргумента перицентра кеплеровской орбиты для задачи Баррара и
переходят в кеплеровские элементы про с=0.
Канонические переменные
«действие-угол» введены в работах [2, 3] и выражены через эллиптические
квадратуры.
В соответствии с ранее
принятыми обозначениями в сферических координатах r, φ, λ функция Гамильтона невозмущённой задачи Баррара может
быть записана в виде
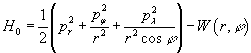 . (14)
. (14)
Здесь канонические
импульсы определены стандартным образом, а потенциал W
определяется формулой (2).
Уравнение
Гамильтона-Якоби
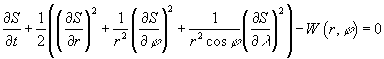 (15)
(15)
даёт полный интеграл, который легко
находится разделением переменных:
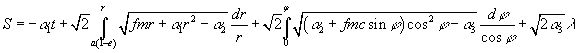 (16)
(16)
В формуле (16)
канонические постоянные α1, α2, α3
выбраны следующим образом:
![]() ,
, ![]() ,
, ![]() . (17)
. (17)
Зная полный интеграл
уравнения Гамильтона-Якоби, определим для данной задачи канонические переменные
«действие» по формулам
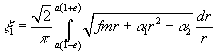 ,
,
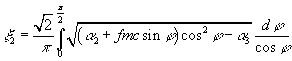 , (18)
, (18)
![]() .
.
В результате
интегрирования получим
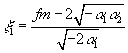 ,
,
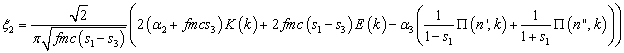 ,
,
![]() , (19)
, (19)
где K(k), E(k), ![]() (n,k) – полные
эллиптические интегралы I, II, III рода
соответственно, а их параметры и модуль соответственно равны
(n,k) – полные
эллиптические интегралы I, II, III рода
соответственно, а их параметры и модуль соответственно равны
![]() ,
, ![]() ,
, 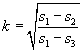 ,
,
причём s1, s2, s3 являются
корнями уравнения
2cs3+ps2-2cs+(2ccos2i-psini)sini=0
и выражаются формулами (10) и (11).
Опуская выкладки,
отметим, что переменные «угол», соответствующие соответствующим переменным типа
«действие», выразятся следующими формулами:
![]() ,
,
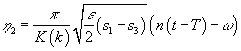 , (20)
, (20)
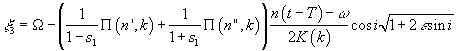 ,
,
где Т
– момент прохождения спутником перицентра, М – средняя аномалия спутника, n – среднее
движение:
![]() .
.
Дифференциальные
уравнения, описывающие возмущённое движение спутника во введённых выше
канонических переменных «действие-угол», будут иметь вид:
![]() ;
; ![]() ; (i=1,2,3) (21)
; (i=1,2,3) (21)
где
Н=Н0+R. (22)
Невозмущённый
гамильтониан ![]() , а пертурбационная функция R задаётся формулой (3), при этом предполагается, что R есть
функция переменных
, а пертурбационная функция R задаётся формулой (3), при этом предполагается, что R есть
функция переменных ![]() (i=1,2,3).
(i=1,2,3).
Дифференциальные
уравнения возмущённой задачи Баррара принимают наиболее простую форму, если вместо
переменных ![]() ввести канонические
переменные L, G, H, l, g, h, подобные элементам Делоне кеплеровского движения и
обращаются в соответствующие элементы при с=0.
Попытка ввести такие переменные была предпринята в [4], однако при введении
переменных была сделана ошибка: вверённые переменные не удовлетворяют условию
каноничности! Введём переменные с помощью равенств
ввести канонические
переменные L, G, H, l, g, h, подобные элементам Делоне кеплеровского движения и
обращаются в соответствующие элементы при с=0.
Попытка ввести такие переменные была предпринята в [4], однако при введении
переменных была сделана ошибка: вверённые переменные не удовлетворяют условию
каноничности! Введём переменные с помощью равенств
L=ξ1+ξ2+ξ3, l=η1,
G=ξ2+ξ3, g=-η1+η2, (23)
H=ξ3, h=η2+η3,
Поскольку, как легко
проверить,
![]() , (24)
, (24)
элементы L, G, H, l, g, h являются каноническими и при с=0 обращаются в соответствующие элементы Делоне кеплеровского
движения.
Уравнения возмущённого
движения в канонических оскулирующих переменных L, G, H, l, g, h будут иметь вид
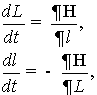
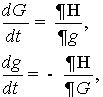
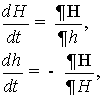 (25)
(25)
причём
![]() . (26)
. (26)
Ясно, что в формуле (26)
![]() - невозмущённый
гамильтониан задачи Баррара, R – пертурбационная
функция(3).
- невозмущённый
гамильтониан задачи Баррара, R – пертурбационная
функция(3).
Введение предложенных
автором переменных существенно упрощает решение задачи интегрируемости
возмущённой задачи Баррара.
Библиографический список.
1.
Barrar R.B. Some remarks on the motion of a satellite of an oblate
planet.// Astron. Journ. 1961. V. 66, №1.
2.
Дёмин В.Г. Движение
искусственного спутника в нецентральном поле тяготения./ М.: Наука, 1968. стр.
122-130.
3.
Конкс В.Я. Канонические
переменные «действие-угол» в задаче Баррара. //Космические исследования, 1985,
т. 23, вып. 3, стр.477-479.
4.
Искакова А.М. Переменные
«действие-угол» в задаче Баррара.// Аналитическая механика тел переменной
массы. Алма-Ата, 1982. стр. 30-36.
5.
Севрюков П.Ф. О
дополнительных аналитических первых интегралах возмущённой задачи Баррара.//
Проблемы механики управляемого движения. Нелинейные динамические системы:
Межвуз. сб. научн. трудов/ Пермь: – Перм. ун-т, 1989. стр. 142-145.
6.
Пуанкаре А. Новые методы
небесной механики// Пуанкаре А. Избранные труды/ М.: Наука, 1971. т. 1, стр.
8-326.