Математическая модель новой  рулевой трапеции автобуса «МАЗ»

Гурвич Ю. А., Лебедев Е.П.

Белорусский национальный технический университет

Под механико-математической моделью понимается  совокупность схемы рулевой трапеции и формализованной связи (математического описания       b=Ф(a,l1,..,lj,g1,..,gm),  где b – угол поворота внешнего управляемого колеса машины; a - угол поворота внутреннего колеса; l1,…,lj – управляемые параметры; j – количество управляемых параметров; g1,…,gm – неуправляемые параметры; m- количество неуправляемых параметров.

Механико-математическая  модель рулевой трапеции
 
 


+
 

β= Ф(a,l1,..,lj,g1,..,gm)
 

=
 

Схема рулевой трапеции (рис. 1)
 
 

 

В литературе приведено большое число различных конструкций рулевых трапеций, которые используются в машинах на пневмоколесном ходу. Соответственно приведены  схемы этих рулевых трапеций. Известна только одна механико-математическая модель – модель четырехзвенной неразрезной рулевой трапеции, впервые полученная академиком Е.А. Чудаковым [1]. Для всех остальных конструкций рулевых трапеций приведены только схемы, а математические описания  β= Ф(a,l1,..,lj,g1,..,gm) отсутствуют. Причём для каждой новой конструкции рулевой трапеции будет свое число звеньев и своя совокупность конструктивных параметров.

 

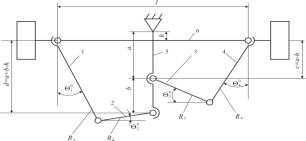
Рисунок 1. Схема несимметричной шестизвенной рулевой трапеции автобуса «МАЗ», колеса которого находятся в нейтральном положении

Постановка задачи. Для расчета параметров шестизвенной рулевой трапеции изображенной на рис.1 необходимо формализовать связь угла поворота наружного колеса  от угла поворота внутреннего колеса a и других управляемых и неуправляемых (конструктивных) параметров  β=β(a,l1,..,lj,g1,..,gm).

На рисунке 1 изображена новая шестизвенная рулевая трапеция автобуса «МАЗ» в исходном положении. На этом рисунке пронумерованы  длины стержней  1 – 5 соответственно через , , , а углы, определяющие направление стержней в начальном положении (до поворота рулевого колеса), обозначены индексом «0»: .

При повороте рулевого колеса автобуса углы  станут другими, и появится угол наклона стержня 5 к вертикали. Обозначим угол, определяющий  направления стержней 1 – 5 в ненулевом положении  (Рис. 2).

 

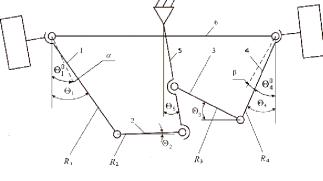
Рисунок 2. Схема несимметричной шестизвенной рулевой трапеции автобуса «МАЗ», колеса которого находятся  в повернутом положении

 

Штриховыми линиями на рис. 2 показаны начальные положения стержней 1 и 5. При повороте управляемого внутреннего колеса автобуса влево на угол  стержни 1, 4 и 5 будут вращаться против часовой стрелки, а углы  и  будут соответственно     равны:  , , , .

Для расчета параметров шестизвенной рулевой трапеции требуется определить зависимость угла поворота наружного колеса  от угла поворота внутреннего колеса β=β(a,l1,..,lj,g1,..,gm) и других конструктивных параметров, что эквивалентно определению .

 Определение начальных углов  и   

Определение . Рассматриваем часть трапеции левее стержня 5 (Рис. 1).

Связи: 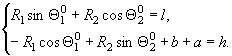                                                           (1)

Система (1) — это система уравнений с двумя неизвестными  и . Из (1) исключим и обозначим . Получим:

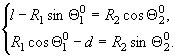                                                                 (2)

 

Возводим в квадрат уравнения (2) и  складываем их. В результате получим:

.                                 (3)

Введем угол  следующим образом:

,                   ,         .

 

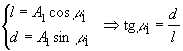Преобразуем выражение (3):

.

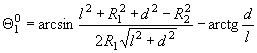Определение . Рассматриваем часть трапеции правее стержня 5 (Рис. 1).

Связи: 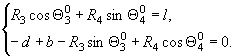                                                               (4)

Из (4) исключим  и обозначим. Получим:

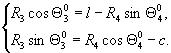                                                              (5)

Исключим из уравнений (5) ,  возведем их в квадрат и сложим:

.                            (6)

Введем угол  следующим образом:

,         ,         .

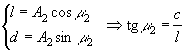Преобразуем выражение (6):

.

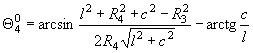Определение зависимости  

 Определение зависимости между  и . Рассматриваем левую часть трапеции (левее стержня 5).

Связи: 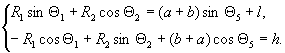                                         (7)

Из выражений (7)  исключим , возведем их в квадрат и сложим:

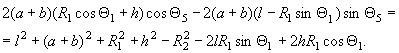              (8)

Определение зависимости между  и .

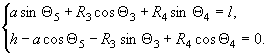Связи:                                              (9)

Из (8) исключим , возведем полученные уравнения  в квадрат и сложим их:

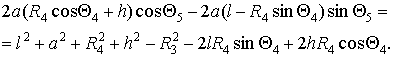               (10)

Исключим  из уравнений (8) и (10).  Уравнение (8) перепишем следующим образом:

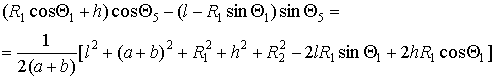    (11)

Введем переменную амплитуду  и :

                            (12)

и примем, что

,

.

Тогда     .                                                        (13)

Преобразуем  уравнение (11) и выразим из него :

.

Окончательно :

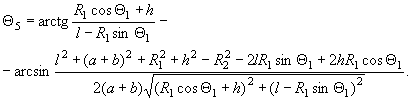            (14)

Преобразуем уравнение (10) таким образом:

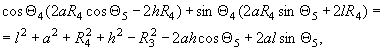
или (делим на ):

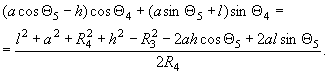                            (15)

Вводим  и переменную амплитуду

,                            (16)

,

.

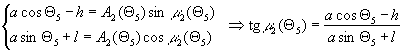Преобразуем уравнение (15) и выразим из него :

,       (17)

где  определяется по формуле (14).

В итоге зависимость угла поворота наружного колеса  от угла поворота внутреннего колеса β=β(a,l1,..,lj,g1,..,gm) примет вид:

,

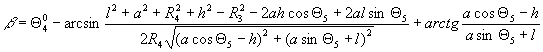где                  ,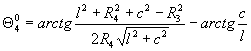

.

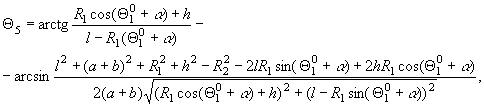
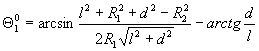Эта рулевая трапеция содержит двенадцать конструктивных параметров: l,, , , , , , , , , в том числе восемь независимых–.

Литература

1. Чудаков Е. А. Теория автомобиля. – М.: Изд. АН СССР, 1961.-462с.