А.И. Долгарев
УРАВНЕНИЕ ВТОРОГО ПОРЯДКА С ЧАСТНЫМИ ПРОИЗВОДНЫМИ,
СВЕДЕНИЕ К УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА.
ЕЩЕ ОДНА КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ
Приведено решение однородного дифференциального уравнения второго порядка с частными производными методом, основанным на геометрических соображениях. Уравнение приведено к системе уравнений первого порядка. Обнаружена еще одна квадратичная форма поверхности.
1. Однородное уравнение второго порядка с частными производными
1.ТЕОРЕМА. Однородное уравнение второго порядка с частными производными
, (1)
коэффициенты которого
подчиняются условиям
,
(2)
имеет своим решением
2-параметрическое семейство функций
, 
постоянные. (3)
Начальные условия вида
(4)
выделяет в (3) единственную поверхность,
проходящую через точку 
и имеющую касательную плоскость
в заданной точке 
.
#
Если функция 
является решением
уравнения (1), то при подстановке функции в (1) должно получиться тождество.
Следовательно, верны равенства
. (5)
Условия (2) означают, что функции (3) удовлетворяют уравнению (1), т.е. это условия интегрируемости уравнения (1): объединяя (2) и (5) имеем
.
Исходя из соображений (5) введем обозначения
, 
.
(6)
В интегрировании функции 
по параметру 
появляется слагаемое,
зависящее от другого параметра – от 
, как постоянное по 
слагаемое. С учетом
(5), очевидно, что выполняются соотношения:
,
.
Приведенные соотношения позволяют
найти функции 
и 
. Действительно, на основании (5),
, 
.
Таким образом,
, 
. (7)
Зная, согласно (6), функции 
, получаем уравнение с полным дифференциалом
.
(8)
Необходимое условие полного дифференциала функции здесь выполняется, т.к.
,
последнее равенство выполняется
тождественно: 
. Решением уравнения (8)
является, с учетом, (6),
.
Слагаемое 
отыскивается на
основе (6) из условия
.
Тем самым, найдено решение (3) однородного уравнения (1). Начальные условия (4) дают частное решение уравнения (1). #
Геометрическое толкование частного решения уравнения в частных производных дано в [1, с. 335 – 336].
В условиях
теоремы 1 при 
вместо (2) имеем
, (9)
что означает 
и 
. По (6), 
, 
, тогда уравнение (8) принимает вид 
и общее решение
уравнения (1) при 
есть
. (10)
2. СЛЕДСТВИЕ. Решением дифференциального уравнения
при условиях (9) является семейство линейных функций (10). #
Решение
(3) дифференциального уравнения (1)
второго порядка в частных производных 
зависит от условий,
налагаемых на его коэффициенты. Условия (2) при 
привели к тому, что
решением уравнения являются линейные функции (10). Другие условия интегрируемости
приводят, как известно, к решениям другого вида. Условия могут иметь вид
, или 
.
Первое из них означает 
, второе – 
.
2. Квадратичная форма поверхности, связанная с ее явным заданием
В окрестности всякой обыкновенной точки евклидовой регулярной поверхности эта поверхность может быть задана явной функцией
, 
,
(11)
см., например, [2, с. 209 – 211] и [3, с. 72 – 73, доказательство теоремы 1]. Имеется векторное задание поверхности (11), связанное с явным заданием
= 
.
(12)
Коэффициенты первой квадратичной формы поверхности (11), а, значит, и (12) есть
, 
, 
; (13)
и коэффициенты второй квадратичной формы поверхности (11) равны
, 
, 
; (14)
при этом детерминант первой квадратичной формы таков
.
(15)
Вторая квадратичная форма поверхности (11) имеет вид
= 
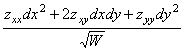. (16)
В числителе последнего выражения
находится квадратичная форма относительно 
:
с коэффициентами
, (17)
это еще одна квадратичная форма регулярной евклидовой поверхности. Согласно (16),
. Доказанная в п.1 теорема 1 означает, что выполняется
3.
ТЕОРЕМА. Коэффициенты (17) квадратичной формы 
поверхности (11) однозначно,
с точностью до положения определяют явно заданную регулярную евклидову
поверхность. # На основании теорем 2 и 1 устанавливается
следующая
4.
ТЕОРЕМА. Коэффициенты (17) квадратичной формы 
определяют коэффициенты первой основной квадратичной формы регулярной
евклидовой поверхности
, 
, 
; .(18)
Полная кривизна поверхности равна
.
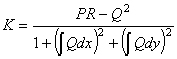(19)
#
Воспользуемся доказательством теоремы 1. Коэффициенты квадратичной формы 
определяют
единственную явно заданную регулярную евклидову поверхность (11), см. теорему
3. По (5) имеем
, 
.
На основании (13) справедливы равенства (18) и
= 
. (20)
В [4], установлено, что
поверхность (11) однозначно определяется коэффициентами ее первой квадратичной
формы. Имея форму 
, получаем поверхность (11) и имея первую квадратичную форму,
получаем (11). В обоих случаях
получается одна и та же поверхность, как показывают соотношения (18) и
(19). #
5.
ТЕОРЕМА. Евклидова регулярная поверхность
(11) определяется с точностью до
положения, если заданы коэффициенты ее второй квадратичной формы 
, 
, 
и детерминант первой квадратичной формы 
. Заданные функции
подчиняются условиям
, 
, 
. (21)
Начальные условия вида (4) выделяют
единственную поверхность, проходящую через точку 
и имеющую касательную плоскость
в заданной точке 
, 
.
#
Поверхность (11), имеющая коэффициентами второй квадратичной формы функции 
и детерминант 
первой квадратичной
формы, такова, что выполняются соотношения (14) и (15) . По второй формуле в (14)
, 
, значит,
, 
. (22)
По первому и третьему соотношениям в (14), имеем первое и второе условия в (21)
, 
.
Третье условие в (21) получаем по функциям (22) и формуле (15).
Заданные начальные условия определяют единственную поверхность (11). #
Оказалось, что регулярная евклидова поверхность (11) однозначно, с точностью до положения, определяется коэффициентами первой квадратичной формы, [4], или же коэффициентами второй квадратичной формы и детерминантом первой квадратичной формы. Это верно для всякой регулярной евклидовой поверхности, т.к. в окрестности обыкновенной точки регулярная поверхность описывается явной функцией (11).
3. Система уравнений второго порядка с частными производными.
Приведение к системе уравнений первого порядка с частными производными
6. ТЕОРЕМА. Однородное уравнение с частными производными второго порядка (1) равносильно системе уравнений второго порядка с частными производными
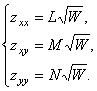(23)
# Формулы (14) записываются в виде системы уравнений (23). Левые части системы (23) удовлетворяют условиям (2), значит, система (23) имеет вид (5). Уравнение (1) можно записать в виде системы уравнений
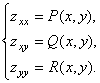
Условия (2) остаются в силе, начальные условия сохраняются. Положим:
.
Всякое решение системы уравнений (23) является решением уравнения (1) и обратно. #
7. ТЕОРЕМА. Коэффициенты второй квадратичной формы поверхности выражаются через коэффициенты первой квадратичной формы поверхности.
# В [5] формулы (13) продифференцированы и получены равенства
, 
, 
, 
. (24)
Так как 
, то с использованием второй формулы из (13) имеем: 
. По второй формуле в (14) находим
. (25)
По первой и третьей формулам в (14) и (13) имеем
, 
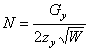. # (26)
В [5] по (25) и (26) получена формула Гаусса
.
Формулы (25), (26) означают, что выполняется
8. ТЕОРЕМА. Все свойства регулярной евклидовой поверхности, основанные на соотношениях, использующих коэффициенты первой и второй квадратичных форм, могут быть выражены через коэффициенты первой квадратичной формы поверхности. #
Подученные соотношения позволяют установить
9.
ТЕОРЕМА. Система уравнений (23) приводится к системе уравнений
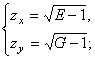(27)
первого порядка, решением
которой является функция 
, находимая по заданным
коэффициентам первой квадратичной формы поверхности в [4].
# По первому уравнению в (23) и первой формуле в (26) имеем:
.
Аналогично получается 
. Кроме того, выполняются равенства
, 
.
Следовательно,
, 
. (28)
Рассматривается поверхность
(11) 
, производные функции 
удовлетворяют
равенствам (23), (13). По последним из них:
, 
, (29)
т.е. 
, 
. Равенства (28), (29) равносильны, приходим к (27), рассматриваемой
в [4]. Система уравнений (23) сводится
к системе уравнений (27). #
На основании теорем 5, 8 и 9 заключаем, что выполняется
10. ТЕОРЕМА. Коэффициенты второй квадратичной формы поверхности не определяют поверхность; кроме коэффициентов второй квадратичной формы должен быть задан детерминант первой квадратичной формы поверхности. #
Литература
- Степанов В.В. Курс дифференциальных уравнений. - М., 1959. - 468 с.
- Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.
- Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. - М.: Наука, 1979. - 560с.
- Долгарев А.И. Система линейных уравнений первого порядка в частных производ-
ных. Задание евклидовой поверхности коэффициентами ее первой квадратичной
формы. // Materiali IX mezinarodni vedecko-praktika conference
«Dni vediy – 2013» -
Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and
Skience”. s.r.o. – 112. С. 32 – 40.
- Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверх-
ностей.//
Materiali IX mezinarodni vedecko-praktika conference «Dni vediy – 2013» -
Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and
Skience”. s.r.o. – 112. С. 55 – 60.