Математика/ 5. Математическое моделирование
к.ф.-м.н. Мухамбетжанов
А.Т., к.ф.-м.н. Искакова А.С.
Евразийский
национальный университет им. Л.Н. Гумилева, Казахстан
Об одном примере численного моделирования решения
линейных краевых задач в системе Matlab
Пусть Ω ограниченная
область, принадлежащая R с гладкой границей ∂Ω. Рассмотрим
задачу
Lu = -u" + q(x)u = f(x),
![]() (1)
(1)
где f(x) ![]() L2(Ω). Пусть -u"=v,
L2(Ω). Пусть -u"=v, ![]() или в операторной
форме A0u = v,
где
или в операторной
форме A0u = v,
где ![]() оператор однозначно
разрешим в пространстве L2
(Ω) с заданными
краевыми условиями. Тогда уравнение
(1) примет вид:
оператор однозначно
разрешим в пространстве L2
(Ω) с заданными
краевыми условиями. Тогда уравнение
(1) примет вид:
![]() (1’)
(1’)
Теорема. Пусть для
любого f(x)![]()
![]() (1) имеет единственное решение и
(1) имеет единственное решение и![]()
![]()
![]() , причем оператор М, определенный по (1’), удовлетворяет
условиям
, причем оператор М, определенный по (1’), удовлетворяет
условиям ![]() ,
, ![]() ,
причем справедливо неравенство cd >1. Тогда для
любого
,
причем справедливо неравенство cd >1. Тогда для
любого![]() последовательность
последовательность![]() , определяемая по
формулам
, определяемая по
формулам ![]() сходится к решению ω. уравнения (1’) причем выполнены оценки
сходится к решению ω. уравнения (1’) причем выполнены оценки ![]() ,
, ![]() где
где ![]() . При
этом функция и =
А-1ω будет решением задачи (1).
. При
этом функция и =
А-1ω будет решением задачи (1).
Пусть ![]() Lu = f при
Lu = f при ![]() , и(0) = и(1) = 0, где L - оператор,
действующий следующим образом
, и(0) = и(1) = 0, где L - оператор,
действующий следующим образом ![]() В этом случае можно взять интегральный оператор А0 с
ядром G (x,t), где G (
В этом случае можно взять интегральный оператор А0 с
ядром G (x,t), где G (![]() ) - функция
Грина задачи
) - функция
Грина задачи ![]() , u(0) = u(1)
= 0. Эта задача
эффективно разрешима и G(
, u(0) = u(1)
= 0. Эта задача
эффективно разрешима и G(![]() ) выписываются явно:
) выписываются явно: 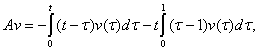
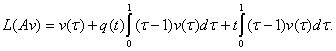
Пусть ![]()
![]() . Рассмотрим задачу
. Рассмотрим задачу
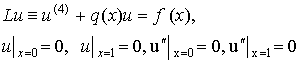
Таким уравнением описывается, например,
поперечный прогиб ![]() балки под действием
распределенной поперечный нагрузки
балки под действием
распределенной поперечный нагрузки ![]() ,
, ![]() . Где балка имеет постоянную жесткость на изгиб и лежит на
упругом основании, реакцию которого определяет слагаемое
. Где балка имеет постоянную жесткость на изгиб и лежит на
упругом основании, реакцию которого определяет слагаемое ![]() ,
, ![]() на интервале
на интервале ![]() .
.
Если балка имеет на
концах опоры, допускающие (в отличие от жесткого защемления) поворот ее
поперечного сечения пропорциональный в этом сечении изгибающему моменту, то в
этом случае граничные условия принимают следующий вид: ![]() .
.
Из этих уравнений при ![]() вытекают условия
жесткого защемления, а при
вытекают условия
жесткого защемления, а при ![]() и
и ![]() - шарнирного опирания. Введем оператор А0, следующим образом: обозначим
- шарнирного опирания. Введем оператор А0, следующим образом: обозначим
![]() = v,
= v,
![]()
или в операторной форме ![]() , где
, где ![]() - оператор однозначно разрешим в пространстве
- оператор однозначно разрешим в пространстве ![]() с заданными краевыми
условиями.
с заданными краевыми
условиями.
Пусть ![]() n n-ное приближенное решение уравнения J(
n n-ное приближенное решение уравнения J(![]() n)=0.
n)=0.
Выберем ![]()
Тогда ![]()
Полученные
результаты численных расчетов в системе Matlab по некоторым значениям
переменной х приведены ниже в таблицах
1-3.
Из таблицы 1 имеем ,что абсалютная
погрешность приближенного значение (![]() =1 и
=1 и
![]() =0.5)
в точке х=0.25 уже при n=2 равна 0.00002 , а относительная погрешность
составляет не более чем 0.0011 или 0.11 процента.
=0.5)
в точке х=0.25 уже при n=2 равна 0.00002 , а относительная погрешность
составляет не более чем 0.0011 или 0.11 процента.
Таблица 1 - Численный расчет
при х=0.25
|
x |
w_n |
e |
J_n |
M w_n - f |
u прибл. |
f(x) = |
|
|
0.25 |
1 |
0.5 |
3.645391 |
3.083496 |
|
-2.05566 |
|
|
1 |
-1.91631 |
|
0.101691 |
0.086016 |
-0.01778 |
|
|
|
2 |
-1.99767 |
|
0.002837 |
0.002399 |
-0.01853 |
|
|
|
3 |
-1.99993 |
|
7.91E-05 |
6.69E-05 |
-0.01855 |
|
|
|
4 |
-2 |
|
2.21E-06 |
1.87E-06 |
-0.01855 |
|
|
|
5 |
-2 |
|
6.16E-08 |
5.21E-08 |
-0.01855 |
|
u точн. |
|
6 |
-2 |
|
1.72E-09 |
1.45E-09 |
-0.01855 |
|
-0.01855 |
|
7 |
-2 |
|
4.79E-11 |
4.05E-11 |
-0.01855 |
|
|
|
8 |
-2 |
|
1.34E-12 |
1.13E-12 |
-0.01855 |
|
|
|
9 |
-2 |
|
3.73E-14 |
3.15E-14 |
-0.01855 |
|
|
|
10 |
-2 |
|
0 |
0 |
-0.01855 |
|
|
Таблица 2- Численный расчет
1 при х=0.5
|
x |
w_n |
e |
J_n |
M w_n - f |
u прибл. |
f(x) = |
|
|
0.5 |
1 |
0.5 |
2.580762 |
3.234375 |
|
-2.15625 |
|
|
1 |
-1.06461 |
|
0.804673 |
1.008468 |
-0.01386 |
|
|
|
2 |
-1.70835 |
|
0.250895 |
0.314437 |
-0.02224 |
|
|
|
3 |
-1.90906 |
|
0.078228 |
0.098041 |
-0.02486 |
|
|
|
4 |
-1.97165 |
|
0.024391 |
0.030569 |
-0.02567 |
|
|
|
5 |
-1.99116 |
|
0.007605 |
0.009531 |
-0.02593 |
|
u точн. |
|
6 |
-1.99724 |
|
0.002371 |
0.002972 |
-0.02601 |
|
-0.02604 |
|
7 |
-1.99914 |
|
0.000739 |
0.000927 |
-0.02603 |
|
|
|
8 |
-1.99973 |
|
0.000231 |
0.000289 |
-0.02604 |
|
|
|
9 |
-1.99992 |
|
7.19E-05 |
9.01E-05 |
-0.02604 |
|
|
|
10 |
-1.99997 |
|
2.24E-05 |
2.81E-05 |
-0.02604 |
|
|
Таблица 3-Численный расчет х=0.75
|
x |
w_n |
e |
J_n |
M w_n - f |
u прибл. |
f(x) = |
|
|
0.75 |
1 |
0,5 |
-1.41595 |
3.250488 |
|
-2.16699 |
|
|
1 |
-1.12393 |
|
-0.41349 |
0.949221 |
-0.01043 |
|
|
|
2 |
-1.74417 |
|
-0.12075 |
0.277196 |
-0.01618 |
|
|
|
3 |
-1.92529 |
|
-0.03526 |
0.080948 |
-0.01786 |
|
|
|
4 |
-1.97818 |
|
-0.0103 |
0.023639 |
-0.01835 |
|
|
|
5 |
-1.99363 |
|
-0.00301 |
0.006903 |
-0.0185 |
|
u точн. |
|
6 |
-1.99814 |
|
-0.00088 |
0.002016 |
-0.01854 |
|
-0.01855 |
|
7 |
-1.99946 |
|
-0.00026 |
0.000589 |
-0.01855 |
|
|
|
8 |
-1.99984 |
|
-7.5E-05 |
0.000172 |
-0.01855 |
|
|
|
9 |
-1.99995 |
|
-2.2E-05 |
5.02E-05 |
-0.01855 |
|
|
|
10 |
-1.99999 |
|
-6.4E-06 |
1.47E-05 |
-0.01855 |
|
|
Литература:
1.
J. M. Ortega, Introduction to parallel and vector solution of linear
systems, Plenum Press, New York, 1982.
2.
H. Trielel, Approximation nubers in function spaces and the distribution
of eigenvalues of some fractal elliptic operators, J. Approximation Theory, 129
(2004), 1-27.