Долгарев А.И.

ДОБАВОЧНЫЕ ВОЗМОЖНОСТИ

ПЕРВОЙ КВАДРАТИЧНОЙ ФОРМЫ ЕВКЛИДОВОЙ ПОВЕРХНОСТИ

Установлено, что коэффициенты второй основной квадратичной формы евклидовой поверхности выражаются через коэффициенты первой квадратичной формы и их производные первого порядка. На основе первой квадратичной формы поверхности ниже выражена нормальная кривизна линий на поверхности, полная и средняя кривизна поверхности, проведена классификация обыкновенных точек регулярной евклидовой поверхности. Указанные понятия являются метрическим и поэтому должны описываться с использованием первой квадратичной формы поверхности, вводящей метрику на поверхности.

1. Задание регулярной евклидовой поверхности явной функцией.

Основные квадратичные формы евклидовой поверхности

Регулярную евклидову поверхность принято задавать векторной функцией

= , , (1)

задание является симметричным. В учебниках по евклидовой дифференциальной геометрии отмечается, что регулярная поверхность может быть описана явной функцией

(2)

в окрестности обыкновенной точки, [1, с. 209 – 211]. Это соответствует параметрическому заданию регулярной евклидовой поверхности (1) в виде векторной функции

= . (3)

Рассматривая поверхности в виде (2), (3), мы имеем дело с их неоднородным и несимметричным заданием.

Первая и вторая основные квадратичные формы регулярной поверхности есть

, ,

, , . (4)

, , , . (5)

В параметризации (3) производные векторной функции таковы

, , , , .

Значения коэффициентов (4) и (5) есть

, , ; (6)

, , . (7)

Полная и средняя кривизна поверхности вычисляется по формулам

, . (8)

Формулы (6) – (7) содержатся в [1, с. 262 – 263], см. также [2, с. 87 – 92], где выявляется большая значимость явного задания евклидовой поверхности.

2. Выражение коэффициентов второй квадратичной формы поверхности

через коэффициенты первой квадратичной формы.

Полная и средняя кривизны поверхности

В [3] найдены значения коэффициентов второй квадратичной формы поверхности

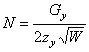, , , (9)

что позволило вычислить полную кривизну поверхности

. (10)

Это еще один вид формулы Гаусса, очень компактный и выражающий полную кривизну регулярной поверхности через коэффициенты первой квадратичной формы поверхности и производные первого порядка этих коэффициентов. Последнее обстоятельство важно тем, что полная кривизна поверхности определена через производные второго порядка функции , задающей поверхность, см. (8) и (5); и в формуле (10) содержатся производные не более чем второго порядка функции . Так как всякая регулярная поверхность в окрестности всякой ее обыкновенной точки задается функцией (2), то теорема 1 из [3] верна в общем случае для регулярной евклидовой поверхности, см. теорему 2 из [3]. Имеет место следующая

1. ТЕОРЕМА. Коэффициенты второй квадратичной формы регулярной евклидо-

вой поверхности выражаются через коэффициенты первой основной квадратичной формы и их производные первого порядка.

# В [3] получены выражения (9). Из (6) находим

, (11)

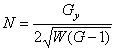, , . (12)

Получены выражения коэффициентов второй квадратичной формы поверхности через коэффициенты первой квадратичной формы поверхности. #

Отметим еще, что выполняются соотношения

= .

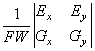2. ТЕОРЕМА. Средняя кривизна регулярной евклидовой поверхности выражается через коэффициенты первой квадратичной формы поверхности и производные первого порядка этих коэффициентов.

# Подставляем во вторую формулу в (8) выражения (12) с учетом (6) и (11):

. # (13)

3. Нормальная кривизна линий на поверхности

На основании теоремы 2 выполняется следующее утверждение.

3. ТЕОРЕМА. В направлении на евклидовой регулярной поверхности нормальная кривизна линий на поверхности вычисляется по формуле

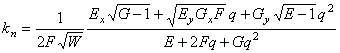, (14)

или .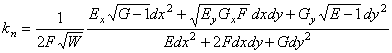

# Известна следующая формула

.

Подставляя сюда значения (12), получаем формулу (14). #

4. ТЕОРЕМА. Нормальная кривизна линий на евклидовой регулярной поверхности выражается через коэффициенты первой квадратичной формы поверхности и производные первого порядка этих коэффициентов. #

4. Об основной теореме теории евклидовой поверхностей

В евклидовой теории поверхностей установлена основная теорема, состоящая в том, что регулярная евклидова поверхность однозначно, с точностью до положения, определяется заданием коэффициентов ее первой и второй квадратичных форм. Впервые теорема доказана российским математиком К.М. Петерсоном в 1853 году, опубликована в 1952 г, [4]. Первая публикация основной теоремы принадлежит О. Бонне, 1867 г. В качестве следствия теоремы Петерсона-Бонне и теоремы 1 настоящей работы получается

5. ТЕОРЕМА. Регулярная евклидова поверхность однозначно, с точностью до положения в пространстве, определяется коэффициентами первой квадратичной формы. #

Основная теорема теории евклидовых поверхностей имеет уточненный вид, как теорема 5. В этом виде теорема установлена в [5], где дано ее доказательство в результате интегрирования системы уравнений с частными производными

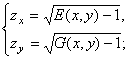
по заданным функциям , удовлетворяющим условиям

,

при заданных начальных условиях и имеет в этой точке касательную плоскость , где . Знаки функций , устанавливаются по заданной функции .

Таким образом, основная теорема теории евклидовых поверхностей в виде 5 установлена двумя независимыми способами как теорема 1 и как теорема 5 настоящей работы. Евклидова поверхность рассматривается в задании (2), и в задании (3); что возможно для всякой регулярной поверхности в окрестности всякой ее регулярной точки, п.1.

5. Классификация обыкновенных точек поверхности

Обыкновенные точки регулярной поверхности принято различать на основе второй квадратичной формы поверхности, см. [1, с. 269 – 274]. Произведем классификацию обыкновенных точек поверхности, используя (9) и (10).

6. ЛЕММА. Для явно заданной поверхности условие означает, что поверхность является цилиндрической; ее полная кривизна .

# По второй формуле в (6): . Равенство возможно только при или , или выполняются оба условия. Если , то = и поверхность (2) является цилиндрической. При поверхность является плоскостью. При выполняется . В этом случае также числитель правой части формулы (10) равен 0. Отношение двух нулей правой части (10) в данном случае равно нулю, в общем случае такое отношение не определено. Случай охватывается формулой (10). #

7. ТЕОРЕМА. Обыкновенная точка евклидовой регулярной поверхности является эллиптической, если в этой точке выражения

и

отличны от нуля и имеют одинаковые знаки; является гиперболической, если указанные выражения отличны от нуля и имеют противоположные знаки; и точка является параболической или точкой уплощения, если

.

# Ввиду (9), вторую квадратичную форму поверхности можно не рассматривать. Вид обыкновенной точки определяет ее полная кривизна. Согласно (10), знак величины совпадает со знаком величины

.

Указанная дробь положительна, если числитель и знаменатель одного знака, и отрицательна, если противоположных знаков. По лемме 6, при имеется параболическая точка или точка уплощения. #

Благодаря формулам (12) возможности первой квадратичной формы поверхности расширились.

6. О внутренней геометрии поверхности

Принято выделять внутреннюю геометрию поверхностей, часто связывая ее с первой квадратичной формой поверхности. По [1, с. 225], «Те геометрические свойства поверхности, которые можно установить, исходя из задания только первой квадратичной формы, относятся к внутренней геометрии поверхности.» Вместе с тем отмечается, что внутренняя геометрия поверхностей изучает изгибание поверхностей. Известны теоремы Либмана и Гильберта: первая о неизгибаемости сферы, вторая – о несуществовании в 3-мерном евклидовом пространстве полной регулярной поверхности отрицательной кривизны, т.е. о неизгибаемости поверхнолсти отрицательной кривизны на плоскость. В связи с результатами пп. 2 – 5 лучше внутреннюю геометрию поверхности связывать только с изгибанием поверхностей.

7. Неоднородность евклидова пространства

Евклидово и галилеево пространства получены на основе аффинного пространства в результате введения в линейном пространстве аффинного пространства либо евклидова либо галилеева скалярного произведения векторов. Объекты аффинного пространства, в частности, линии, обладают аффинными, евклидовыми, галилеевыми и иными свойствами, [6]. Выявить метрические свойства аффинных кривых можно введя соответствующие скалярные произведения векторов аффинного пространства. Для евклидовых кривых определены галиллеева кривизна и галилеево кручение, [7]. Галилеевыми натуральными уравнениями евклидова кривая определяется с точностью до положения в пространстве (обнаруживается это проще, чем для евклидовых натуральных уравнений). Изучение галилеевых свойств евклидовых кривых выявляет неоднородность евклидова пространства, [8]. В евклидовом пространстве, содержащем регулярные кривые, существует 2-мерное инвариантное направление – это направление плоскости галилеевых кривизн евклидовой кривой. Плоскости галилеевых кривизн всех регулярных евклидовых кривых параллельны между собою. В движениях евклидова пространства указанное 2-мерное направление инвариантно, [8]. Рассмотрение регулярных евклидовых поверхностей в явном задании естественно для неоднородного пространства.

8. О значимости полученных выше фактов

В формуле (10) присутствует некоторая неопределенность, преодолеваемая простыми исследованиями, лемма 6. Вторая из формул (12) и формулы (13), (14) содержат двузначные выражения вида . При рассмотрении вопросов, связанными с этими формулами, нужно выбрать знаки таких выражений в каждой обыкновенной точке поверхности. Следствия таких формул могут зависеть от знаков двузначных выражений. Но один вывод бесспорен. Величины, характеризуемые формулами (13), (14), выражены через коэффициенты первой квадратичной формы поверхности и производные этих коэффициентов. Таким образом, выполняется

8. ТЕОРЕМА. Все свойства поверхности, выраженные через коэффициенты первой и второй квадратичных форм поверхности, выражаются только через коэффициенты первой квадратичной формы и их производные. #

Пример выбора знаков у величин , по заданной величине , рассмотрен в [5]; рассмотрения в [5] дают однозначно определенный результат. Формулы (12) – (14) имеют принципиальный характер, а чтобы не выбирать каждый раз знаки выражений , , надо величины вычислять с использованием второй квадратичной формы поверхности, которая вместе с полученными результатами присутствует в теории поверхностей.

Литература

1. Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.
2. Дубровин Б.А, Новиков С.П., Фоменко А.Т. Современная геометрия. //М.: Наука – 1979, 760с.
3. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхно

стей. Materiali IX mezinarodni vedecko-praktika conference «Dni vediy – 2013» - Dil

32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and

Skience”. s.r.o. – 112. С. 55 – 60.

4. Петерсон К.М. Об изгибании поверхностей. Рассуждение на соискание степени кандидата.– В сб. Историко-математические исследования. Вып.V, 1952, с.87 – 133.
5. Долгарев А.И. Система линейных уравнений первого порядка в частных производ-

ных. Задание евклидовой поверхности коэффициентами ее первой квадратичной

формы. // Materiali IX mezinarodni vedecko-praktika conference «Dni vediy – 2013» -

Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and

Skience”. s.r.o. – 112. С. 32 – 40.

6. Долгарев А.И. О геометрии 3-мерного действительного многообразия. – Вестник Татарского государственного гуманитарно-педагогического университета. – Казань, 2011, вып. 1(23). – С. 2 – 15.

7. Долгарев А.И., Долгарев И.А. Некоторые приложения галилеевых методов. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2009, № 2(9), с. 39 – 59.

8. Долгарев А.И. Различные по Ф. Клену евклидовы геометрии: элементарная и диф-

ференциальная.// Materialy IX Miedzynarodowej naukowi-praktycznej konferencji

“Strategiczne pytania swiatowej nauki – 2013” Volume 28. Matematyka. Fizyka.

Nowoczesneinformacyjne technologie.: Przemysl. Nauka i studia – 96 str. C. 3 – 8.