А.И. Долгарев

ОПРЕДЕЛЯЕМОСТЬ ЕВКЛИДОВОЙ КРИВОЙ

ВЕКТОРОМ ГАЛИЛЕЕВОЙ КРИВИЗНЫ

Известна задача И. Ньютона, согласно которой по заданному полю ускорений движения материальной точки требуется указать траекторию движения точки. Траектория движения точки описывается векторной функцией , ускорение движения есть вектор , причем

, время.

Задача И. Ньютона относится к геометрии Галилея-Ньютона, ее геометрической основой является геометрия Галилея. Решению задачи И. Ньютона В.И. Арнольд посвятил книгу [1], в которой анализируются многие геометрии с целью указать такую из них, средствами которой задача решается. На с. 26 в аннотации к § 5 В.И. Арнольд констатирует результаты своих исследований следующим утверждением: ”Анализ общей потенциальной системы с двумя степенями свободы выходит за рамки возможностей современной науки.” Пространство-время Галилея В.И. Арнольд тоже анализирует, [1, c. 12 – 20], но ко времени написания книги [1] геометрия Галилея была создана лишь для 2-мерного случая в работах Н.М. Макаровой, см. [2]. 3-мерная геометрия появилась лишь в 2003 году, [3], изложение геометрии Галилея содержится в [4, с. 46 – 101]. На основе геометрии Галилея решение задачи И. Ньютона для движения с двумя степенями свободы дано в [5]. (Число степеней свободы движущейся материальной точки совпадает с размерностью евклидова пространства, в котором лежит траектория движения.) Для движения с тремя степенями свободы решение содержится в [6].

1. События. Галилеевы свойства

1.1. Мир – пространство событий

Пусть событие , состоящее в том, что точка рассматривается в момент времени . Множество всех событий есть Мир, совпадающий с , где поле действительных чисел. Величина является временной составляющей события , величины являются пространственными составляющими события . Нужна геометрия Мира. Для этого выбираются правила оперирования с событиями. Поступим по аналогии с построением аффинной геометрии на множестве . Выбор размерности 3 не является принципиальным, можно говорить о произвольной размерности . В аффинной геометрии тройки рассматриваются как векторы, т.е. считается линейным пространством над . Вместе с тем тройки рассматриваются как точки, задано отображение пар точек в линейное пространство , удовлетворяющее аксиомам Г. Вейля, т.е. является аффинным пространством с линейным пространством .

На множестве известны разнообразные операции, см., например [4], и множество является алгебраической структурой с выбранными операциями – линейным пространством над , некоммутативным растраном над и т.д.. Выберем линейную коммутативную операцию над событиями, назовем ее сложением, используем символ +, с ней связана внешняя операция умножения троек на действительные числа. Считаем, что алгебраическая структура есть линейное пространство над .

1.2. Галилеево векторное пространство

На множестве задаем операции

+ = , =, .

В результате получено линейное пространство =. Галилеевым скалярным произведением векторов = и = называется число

=

Галилеевым модулем вектора называется число ,

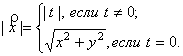(1)

Согласно [7, с. 41], это квазинорма векторов из . Линейное пространство превратилось в галилеево векторное пространство . Первые компоненты векторов из являются временными, вторые и третьи – пространственными. Векторы = евклидовы и составляют евклидово векторное пространство .

В отображении имеем галилееву векторную функцию

= , . (2)

При отображении временного интервала время сохраняет свой временной смысл, оно не превращается в функцию от времени; пространственные компоненты и являются функциями от времени , , так как с течением времени положение материальной точки на плоскости может измениться. Дифференцирование галилеевых векторных функций производится покомпонентно: = , = , … Скорость течения времени считается постоянной: , не существует ускорения течения времени. Пространственные компоненты векторной функции считаются евклидовыми, поэтому и дифференцируются как евклидовы функции.

1.3. Пространство-время Галилея

При введении галилеева скалярного произведения векторов в линейном пространстве аффинного пространства , аффинное пространство становится пространством-временем Галилея и обозначается . Аффинные линии становятся галилеевыми линиями пространства . Галилеево скалярное произведение векторов позволяет выявлять галилеевы свойства линий .

Паре точек , где , = аффинного пространства соответствует вектор . Галилеева длина вектора , согласно (1), есть

=

Первые компоненты событий являются временными, вторые и третьи – пространственными. События = одновременны с событием . Множество событий, одновременных с событием , является евклидовой плоскостью в пространстве-времени Галилея , уравнение этой плоскости . События из есть точки в галилеевом пространстве . Через каждую точку пространства-времени Галилея проходит единственная евклидова плоскость.

1.4. Кривые в пространстве-времени Галилея

Функцию (2) считаем не менее трех раз дифференцируемой. Выполняются условия: , векторы и не коллинеарны. Кривые пространства , описываемые функциями (2) и удовлетворяющие перечисленным условиям, называются регулярными.

Пространственная составляющая события = является материальной точкой = . Линия (2) называется мировой линией события , проекция = мировой линии в евклидову плоскость пространства-времени является траекторией движения материальной точки .

Для двух событий и , , лежащих на мировой линии , по (1) имеем

.

В связи с этим, время есть галилеево расстояние по мировой линии от некоторого события этой линии. Параметризация (2) мировой линии события = является естественной; .

Кривизна галилеевой кривой (2) в естественной параметризации равна модулю вектора второй производной функции :

, , , (3)

см. (1), здесь временная компонента равна нулю, [4М, с. ]; кручение кривой (2) определяется из соотношения

,

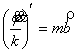где так называемая каппа-функция евклидова вектора , [4М, с. ]

, , , . (4)

Кривизна галилеевой кривой (2) определена по аналогии с кривизной евклидовой кривой в естественной параметризации. Вектор называется вектором галилеевой кривизны линии (2).

В геометрии пространства-времени Галилея выполняется следующая основная теорема теории кривых.

Заданные на интервале функции кривизны и кручения галилеевой кривой определяют кривую (2) на интервале с точностью до положения в пространстве-времени , [8].

По формулам (3) и (4) получена система дифференциальных уравнений

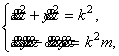(5)

решением которой являются компоненты функции (2), задающей кривую. По первому уравнению системы (5) записываем функции

, , где . (6)

Проверка показывает, что функции (6) удовлетворяют и второму уравнению системы (5). Решение системы уравнений (5) получается в интегрировании функций (6). Начальные условия выделяют единственную кривую , проходящую через данную точку в направлении данного вектора . Тем самым, установлена

1. ТЕОРЕМА О КРИВИЗНЕ. Регулярная кривая галилеева пространства

однозначно, с точностью до положения, определяется вектором кривизны кривой. #

1.5. Решение задачи И. Ньютона для движения с двумя степенями свободы

Пусть материальная точка движется по плоской траектории = , вектор ускорения движущейся точки. Считается, что задано плоское векторное поле , требуется найти траекторию движения . Рассматриваем событие =, состоящее в том, что точка = движется во времени с заданным ускорением , мировая линия движущейся точки есть (2) = , компоненты мировой линии предстоит найти. По определению ускорения движения по траектории, имеем

=, т.е. , .

Кроме того, траектория движения точки отыскивается в результате решения системы уравнений (5), сводящейся к уравнениям (6). Согласно теореме 1 о кривизне, выполняется

2. ТЕОРЕМА. Траектория движения материальной точки с двумя степенями свободы определяется однозначно, с точностью до положения, вектором ускорения.#

Решение задачи И.Ньютона содержится в [5]. Траекторию движения можно найти и интегрируя уравнения , .

2. Метрические свойства кривых

2.1. Евклидовы и галилеевы свойства линий

Согласно [9], линии аффинного пространства обладают метрическими свойствами, однако средствами аффинной геометрии они не выявляются. При введении в линейное пространство аффинного пространства евклидова скалярного произведения векторов, выявляются евклидовы свойства линий ; при введении в галилеева скалярного произведения векторов, выявляются галилеевы свойства линий . Таким образом, всякая регулярная линия обладает как евклидовыми, так и галилеевыми свойствами. Имеется единая геометрия многообразия , ограничение размерности несущественно.

2.2. Галилеевы кривизны евклидовой кривой

В [10] определены галилеева кривизна и галилеево кручение евклидовой кривой. Рассматривается регулярная евклидова кривая

=, . (7)

Условия регулярности кривой означают, что покомпонентные функции обратимы. Пусть . Параметризация (7) заменяется параметризацией

= , (8)

которая называется выделенной, она совпадает с естественной параметризацией (2) галилеевой кривой; параметр может иметь смысл, отличный от временного. Параметризации (8) соответствует задание линии (7) как линии пересечения двух цилиндрических поверхностей:

каждая из них задана явной функцией параметра .

Галилеевой кривизной евклидовой линии (8) называется величина

= = ; (9)

галилеевым кручением евклидовой кривой (8) называется величина

= = , (10)

ср. с определениями (3) и (4) для галилеевой кривой (2). Справедлива теорема о галилеевых натуральных уравнениях евклидовой кривой.

3. ТЕОРЕМА. Регулярная евклидова кривая функциями галилеевых кривых и определяется однозначно, с точностью до положения в пространстве.

# Это есть основная теорема теории галилеевых кривых, сформулированная для евклидовых кривых, т.е. для одних и тех же кривых, рассматриваемых в различных условиях – в условиях евклидова и галилеева скалярных произведения векторов. #

2.3. Решение задачи И. Ньютона для движения с тремя степенями свободы

Этот случай задачи И. Ньютона содержится в [6]. Пусть материальная точка = движется по траектории (7) под воздействием ускорения = . Считаем функцию дифференцируемой и . Тогда покомпонентные функции обратимы, пусть существует функция . Приходим к заданию ускорения в виде (8) = . Система дифференциальных уравнений вида (5)

,

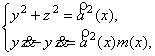
имеет своим решением функции , где и движение по траектории = происходит под воздействием ускорения = . По функции , обратной к , имеем функцию . Подставляя ее в компоненты функции , имеем функцию . Получен аналог теоремы 2:

4. ТЕОРЕМА. Траектория движения материальной точки с тремя степенями

свободы однозначно, с точностью до положения, определяется вектором ускорения движения. #

Вместе с тем, траектория движения отыскивается в результате интегрирования дифференциальных уравнений:

, , .

2.4. Определяемость евклидовой кривой

Евклидова регулярная кривая определяется заданием ее галилеевых натуральных уравнений, теорема 3. С учетом решения задачи И. Ньютона справедлива

5. ТЕОРЕМА. Регулярная евклидова кривая однозначно, с точностью до положе-

ния в пространстве, определяется вектором галилеевой кривизны.

# Евклидову кривую рассматриваем в выделенной параметризации (8). Пусть задан вектор галилеевой кривизны

(11)

евклидовой кривой (8) . Галилеева кривизна линии (8), согласно (9), есть

.

По компонентам данного вектора вычисляется галилеево кручение (10)

.

Имеем систему дифференциальных уравнений вида (5)

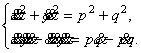(12)

Имеем функции вида (6)

, , , (13)

Интегрируя уравнения (13), находим компоненты кривой , обладающей вектором галилеевой кривизны (11). Соответствующие начальные условия выделяют из решений уравнений (13) единственную кривую, проходящую через точку в заданном направлении . Правые части уравнений (13) есть функции компонент данного вектора галилеевой кривизны кривой (8). Для получения кривой (8) достаточно знать компоненты вектора (11). Но по первому уравнению системы (12) вместо (13) можно написать уравнения

.

Их решения дают функции . #

Итак, для получения евклидовой кривой (8) можно задать две функции и галилеевых кривизн линии (8) или две функции компонент вектора галилеевой кривизны этой кривой. Для регулярной евклидовой кривой (7) вектор галилеевой кривизны есть

.

Если задан вектор , то вектор отыскивается в результате решения дифференциальных уравнений

.

Использованная литература

1. Арнольд В.И. Математические методы классической механики. – М.: Наука, 1989. – 472с.
2. Макарова Н.М. Двумерная неевклидова геометрия с параболической метрикой длин и углов: Дис. ... канд.физ.-мат.наук. - Л., 1962.
3. Долгарев А.И. Элементы дифференциальной галилеевой геометрии и одуль галилеевых преобразований. – Саранск: Средневолжское математическое общество, 2003, препринт 63. – 116с.
4. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.
5. Долгарев А.И. Натуральные уравнения галилеевой кривой и решение уравнения Ньютона для движения с двумя степенями свободы.// Материали за VII Международна научна практична конференция «Найновите постижения на европейската наука» – 2011. Том 37. Математика. София. «Бял ГРАД-БГ» ООД 2011. – С. 5 – 15.
6. Долгарев А.И. Решение задачи Ньютона для движения с тремя степенями свободы.- Materialy VIII mezinarodni vedecko-praktika conference “Veda a vznik – 2011 - 2012”. Dil 28. Matematika,Fizika, Moderni informacni technologie. Praga,2012, p. 3 – 8.
7. Розенфельд Б.А., Замаховский М.П. Геометрия групп Ли. Симметрические, параболические и периодические пространства. – М.: МЦНМО, 2003.- 560с.

8. Долгарев А.И. Натуральные уравнения кривых 3-мерных одулярных галилеевых пространств// Дифференциальная геометрия многообразий фигур. Межвуз. тем. сб. научн. тр. Вып. 36. – Калининград: КГУ, 2005. – С. 31 – 36.

9.Долгарев А.И. О геометрии 3-мерного действительного многообразия. – Вестник Татарского государственного гуманитарно-педагогического университета. – Казань, 2011, вып. 1(23). – С. 2 – 15.

10. Долгарев А.И., Долгарев И.А. Некоторые приложения галилеевых методов. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2009, № 2(9), с. 39 – 59.