Т.ғ. докторы, профессор Ә.К. Байдібеков

Студент Т.С. Набидуллина

Л.Н.Гумилев атындағы Еуразия Ұлттық Университеті, Қазақстан

ТӨРТ РЕТТІ ҚИСЫҚ СЫЗЫҚТАРДЫҢ ЖАҢА САЛЫНУ ЖОЛДАРЫ

Сызба геометрияда қисық сызықтар нүкте мен түзу сызықтан кейінгі қарапайым геометриялық элемент болып саналады. Қисық сызықтар күнделікті өмірде әр түрлі жағдайда кездесіп отырады. Бұл қисық сызықтардың ішінде төрт ретті қисықтардың нүкте мен түзуден және екі ретті және үш ретті қисық сызықтардан кейінгі көп таралған геометриялық элементтер болып табылады.

Төрт ретті қисықтардың математикада, техникада, техникалық ғылымдарда алатын орны ерекше. Бұл - қисықтардың геометрикалық, механикалық және басқа да қасиеттерін зерттеумен өткен ғасырлардың көрнекті математиктері айналысқаны тарихтан белгілі. Осы төрт ретті қисықтардың тамаша қасиеттерін қазіргі кезде де түрлі механизмдерде, оптикада, кеме, көліктер мен ұшақтар жасауда, сәулет–құрылыс ғимараттарын салғанда да кеңінен қолданылады.

Қисықтардың көмегімен қайсыбір үрдістің бағытын көрнекті түрде қадағалауға, тәжірибе нәтижесін бейнелеуге, қайсыбір функционалдық тәуелділіктің мәнін жақсырақ түсінуге, әзірге аналитакалық өрнектерді табылмаған заңдылықтарды зерттеуге, кейбір ғылыми және инженерлік есептерді, әсіресе олардың шешуі күрделі немесе қолайсыз үлкен математикалық аппараттарды қолдануды қажет ететін есептерді шешуге, бұйымдарға мүмкіндігінше тиімді әрі көркем тұлға беруге және т.б мүмкіндік туады. Сызба геометрияда жазықтық қисық сызықтарының дәрежелері қисық сызықтың түзу сызықпен қиылысу нүктелері арқылы анықталатынын белгілі. Біз осы сызба геометрияда диссертация қорғаған техника ғылымының докторы, профессор Әуез Кеңесбекұлы Бәйдібековтың жасаған биквадратты түрлендіру әдістерінің ішіндегі 5-ші түрлендіруін негізгі зерттеу аппараты ретінде алып отырмыз.

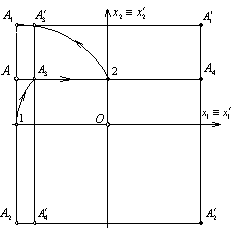
1-сурет

Профессор Ә.К.Байдібеков жалпы жағдайда орналасқан түзу сызықтарды зерттеп, төрт ретті түзу сызықтарды тапқан болатын (2-сурет). Бұл әдіс бойынша табылған төрт ретті қисық сызықтар құрылыс мамандығында қолданғанын диссертациялық жұмыстан оқып көрдім.

Т.ғ.д. Ә.К.Байдібековтың диссертациялық еңбегінде осы әдістің көмегімен әртүрлі төрт ретті жаңа қисықтар шыққанын көре отырып, осы әдісті әрі қарай дамытуға өз үлесімізді қоссам деп шештік.

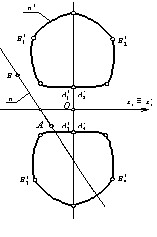
2-сурет

Ал біз биквадратты түрлендіру әдістерінің ішіндегі 5-ші түрлендіруі негізінде түрлендіретін түзу сызықтың прообразын графигіміздің центрі арқылы өткіземіз (3-сурет).

Мысал ретінде төрт ретті қисық сызықтардың ішіндегі қарапайым түрі түзуді аламыз. Биквадратты түрлендіру әдістерінің ішіндегі 5-ші түрлендіруінің алып, көмегімен төрт ретті қисық сызықтарды табуға тырыстық (3 және 4-суреттер).

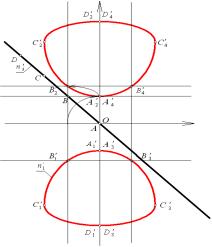
3-сурет

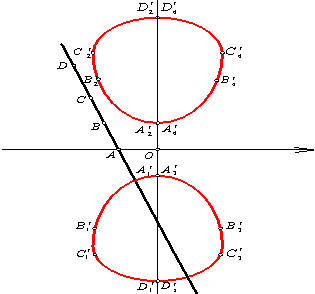
4-сурет

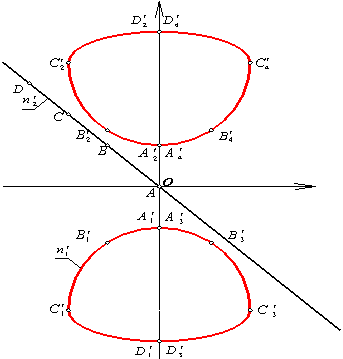
5-сурет

Қорыта келгенде, біздің мақсатымыз, біріншіден, студенттерге төрт ретті қисық сызықтардың шығу жолдарымен таныстыру. Екіншіден,осы биквдратты түрлендіруді пайдаланып, өзімізге жаңа қисықтарды тауып, студенттердің ғылымға деген құштарлығын арттыру болып табылады.

Пайдаланылған әдебиеттер:

1. Ә.К. Бәйдібеков. Развитие теории квартетичных соответствий и их применение. -М.: Изд. Компания «Спутник+». 2005. -95 с.