Технічні науки 10. Гірництво

Канд. техн. наук Василишин Я.В., Василишин В.Я.

Івано-Франківський національний технічний університет нафти і газу

ОПТИМІЗАЦІЯ ГЕОМЕТРИЧНИХ ПАРАМЕТРІВ РІЗЬБОВОЇ ЧАСТИНИ НАСОСНО-КОМПРЕСОРНИХ ТРУБ

При дослідженні різьбового з’єднання насосно-компресорних труб (НКТ) стараються знайти таке поєднання його геометричних параметрів, щоб при найменших затратах матеріальних засобів та часу отримати найбільш точну і повну інформацію про вплив кожного досліджуваного параметра на функцію відгуку для ніпеля та для муфти.

Для дослідження різьбової частини НКТ, враховуючи пріоритетність показників якості різьби [1], виберемо такі геометричні параметри:

- для ніпельної частини (табл.1): – крок різьби; – висота профілю різьби; – кут зовнішньої фаски; товщина стінки;

Таблиця 1 – Коефіцієнти вагомості та пріоритетність показників якості різьби ніпельної частини НКТ

Пріо-рітет-ність	Одиничні показники якості різьби та їх геометрична інтерпретація		Дисперсії одиничних показників	Коефіцієнти вагомості
1		крок різьби	=0,000002	=0,680471745
2		висота профілю різьби	=0,000004	=0,319233658
3		кут зовнішньої фаски	=0,006232	=0,000180404
4		товщина стінки	=0,009707	=0,000057048
5		відхилення конусності різьби	=0,0132729	=0,0000343505
6		зовнішній діаметр труби	=0,116404	=0,000009658
7		глибина внутрішньої фаски	=0,162788	=0,000006906
8		кут нахилу бічних сторін	=0,457861	=0,000002455
9		натяг різьби	=0,545496	=0,0000020609
10		довжина різьби	0,656438	=0,0000017127
Дисперсія комплексного показника якості ніпельної частини різьби НКТ:

- для різьби муфт (табл.2): кут різьби; ширина зовнішньої фаски; висота профілю різьби муфти; відхилення конусності різьби.

Таблиця 2 – Коефіцієнти вагомості та пріоритетність показників якості різьби муфт НКТ

Пріорі-тет-ність	Одиничні показники якості різьби та їх геометрична інтерпретація		Дисперсії одиничних показників	Коефіцієнти Вагомості
1		кут різьби	=0,0000145	=0,862000122
2		ширина зовнішньої фаски	=0,0000451	=0,292933
3		висота профілю різьби муфти	=0,000091	=0,137351668
4		відхилення конусності різьби	=0,0466	=0,000268219
5		діаметр циліндричної виточки муфти	=0,121235	=0,00014158
6		глибина циліндричної виточки муфти	=0,225232	=0,0000555511
7		зовнішній діаметр муфти	=0,23645	=0,0000528611
8		довжина муфти	=0,305	=0,0000409803
9		ширина торцевої площини муфти	=0,43278	=0,0000290674
10		кут зовнішньої фаски	=0,63645	=0,0000196386
11		кут нахилу бічних сторін профілю різьби	=0,81685	=0,0000153015
12		кут переходу від циліндричної виточки муфти до різьби	=0,86255	=0,0000144908
13		натяг різьби муфти	=2,37	=0,0000052738
Дисперсія комплексного показника якості різьби муфт НКТ буде дорівнювати:

Таким чином, число незалежних змінних приймає значення

Функції відгуку відповідно будуть:

Функція відгуку має вигляд

де - коефіцієнт регресії, що називається лінійним ефектом змінної ;

– парна взаємодія факторів та .

Математичну модель 2-го порядку у загальному вигляді можна записати так:

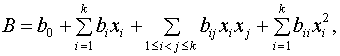
де – вибіркова оцінка функції, що вивчається;

– вибіркові коефіцієнти регресії (оцінки) для генеральних значень коефіцієнтів регресії ,, ;

- незалежні змінні; – загальне число незалежних змінних.

При проведенні дослідів використовуються математичні методи планування, за допомогою яких розкривається вплив досліджуваних геометричних параметрів та їх взаємодії на міцність та навантажувальну здатність різьбової частини НКТ.

Математична обробка даних дозволяє знайти коефіцієнти рівняння регресії за формулами:

; ;

, ;

.

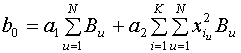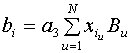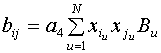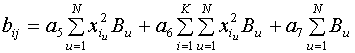Порядок проведення статистичного аналізу отриманого рівняння регресії:

1. Визначається дисперсія досліду за формулою

,

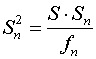де ,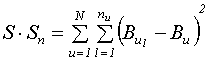

- експериментальні дані при повторенні u-ої серії дослідів;

- середнє значення експериментальних даних для u-ої серії,

визначається за формулою ;

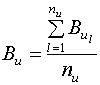– число паралельних дослідів в u-ій серії;

– число серій дослідів, що відрізняються один від одного;

– число степенів вільності, що являє собою різницю між загальним числом дослідів в експерименті і числом серій дослідів в ньому .

2. Визначається дисперсія похибки визначення коефіцієнтів регресії

; ; ; ,

де .

3. Визначаються довірчі інтервали коефіцієнтів регресії

; ; ; ,

де – табличне значення критерія Стьюдента; вибирається за заданою довірчою вірогідністю і числом степенів вільності , знайденому при оцінці дисперсії .

Коефіцієнт регресії можна вважати значимим із заданою довірчою вірогідністю, якщо .

При порушенні цієї нерівності коефіцієнт незначимий і виключається з рівняння регресії.

4. Визначається дисперсія, що характеризує неадекватність моделі

,

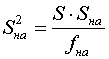де 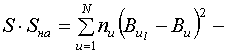сума квадратів, яка визначає неадекватність представлення результатів експеримента;

– число степенів вільності, що відповідає і є різницею між числом серії дослідів в експерименті і числом значимих коефіцієнтів в перетвореному рівнянні регресії.

Перевірка гіпотези про адекватність представлення результатів експерименту рівнянням регресії здійснюється за допомогою -критерія Фішера .

Розрахункове значення F-критерія порівнюється з табличним при вибраному рівні значимості і числі степенів вільності та . Якщо , то гіпотеза про адекватність відкидається.

Після знаходження адекватної графоаналітичної моделі необхідно дослідити поверхню відгуку в околі оптимуму методами аналітичної геометрії і лінійної алгебри, які дозволяють встановити форму цієї поверхні і окреслити шляхи оптимізації даного процесу [2].

Дослідження поверхні відгуку починається з перетворення рівняння другого порядку в канонічну форму, тобто знаходження рівняння, що характеризує форму поверхні і дозволяє поділити всі - вимірні поверхні відгуку на: 1) такі, що мають екстремум; 2) мінімаксні; 3) типу зростаючого підвищення (“гребня”).

Така методика канонічного перетворення може бути повністю використана при аналізі багатовимірних поверхонь відгуку за допомогою двовимірних перерізів. У цьому випадку для дослідження впливу двох яких-небудь факторів на функцію відгуку всі решта незалежні змінні в рівнянні фіксуються на оптимальних рівнях, що дозволяє перейти до дослідження рівняння кривих 2-го порядку і значно спростити розрахунки.

Література

1. Кононенко М.А., Семенюк С.С., Габльовська Н.Я., Луцишин Т.І. Аналіз якісних показників різьбової частини насосно-компресорних труб // Розвідка і розробка нафтових і газових родовищ. – 2007. – №6. – С.50–55.

2. Василишин В.Я. Алгоритм оптимізації геометричних параметрів різьбових з’єднань із вставним витком за умов міцності та навантажувальної здатності / В.Я.Василишин // Розвідка та розробка нафтових і газових родовищ. – 2006. – №4(21). – С.82 – 85.