Технические науки /Отраслевое машиностроение
К.т.н. Харламова С.П., к. т. н. Алехин С.Н.,
магистрант первого года обучения Плескачев В.Н.
Институт сферы обслуживания и предпринимательства
федеральное государственное бюджетное образовательное учреждение высшего
профессионального образования «Донской государственный технический университет»
(ИСО и П (филиал) ДГТУ)
К методу анализа влияния нестационарного температурного режима
холодильной камеры на энергетические характеристики бытовых холодильных приборов
Результаты стендовых испытаний режимов работы бытовых
холодильных машин параметрического ряда фирмы «Атлант» (г. Минск, республика
Беларусь) с двухпозиционным температурным реле подтверждают влияние колебаний
температуры объектов холодильной камеры на энергетические характеристики машин.
На основе теоретических исследований цикличной
работы бытовых холодильных приборов компрессионного типа [1] авторами данной
статьи разработаны методика аналитического анализа влияния температуры
окружающего воздуха и места установки терморегулятора на формирование
температурного поля в холодильной камере.
Цикл работы автоматической холодильной машины
состоит из двух режимов [рис.1]: рабочего–компрессор включён, температура
холодильного агента и стенок испарителя понижается от ![]() , (при пуске) до
, (при пуске) до ![]() (при остановке);
нерабочего – компрессор выключен.
(при остановке);
нерабочего – компрессор выключен.
В
нерабочем режиме от охлаждаемого объекта отводиться тепло и температура стенок испарителя
повышается от ![]() до
до ![]() . Температура испарителя циклично колеблется в пределах
. Температура испарителя циклично колеблется в пределах ![]() , и изменяется практически по экспоненте.
, и изменяется практически по экспоненте.
При
естественной конвекции воздуха в холодильной камере на перемещение охлаждённого
воздуха по объёму камеры требуется определённое время. При этом, чем дальше от
испарителя расположено термореле, тем больше время запаздывания включения
компрессора и тем больше будет отличаться амплитуда колебаний температуры
камеры ![]() от дифференциала
термореле
от дифференциала
термореле![]() .
.
При
разработке методики приняты следующие общепринятые допущения:
– пуск и остановка компрессора осуществляется
двухпозиционным термореле по температуре кипения холодильного агента;
– внутренние и наружные поверхности
камеры изотермические, температурное поле одномерное, стационарное;
– воздух и поверхности находящихся в
камере объектов во всех точках камеры в каждый момент времени имеют одну и ту
же температуру ![]() и водяной эквивалент
и водяной эквивалент
![]() ;
;
– текущее значение температуры поверхности
испарителя ![]() ;
;
– температура поверхности испарителя
![]() с водяным
эквивалентом В,
с водяным
эквивалентом В, ![]() в каждый момент
времени одинакова во всех точках поверхности и равна
в каждый момент
времени одинакова во всех точках поверхности и равна![]() .
.
Приняты
неизменными:
– площадь поверхностей ограничений ![]() ;
;
– термическое сопротивление
ограждений ![]() ,
, ![]() ;
;
– площадь внутренних поверхностей
камеры, ![]() ;
;
– площадь поверхностей испарителя ![]() ,
, ![]() ;
;
– коэффициент теплоотдачи от воздуха
камеры к поверхности испарителя ![]() ,
,![]() .
.
– коэффициент теплоотдачи от стен
камеры к воздуху камеры ![]() ,
,![]()
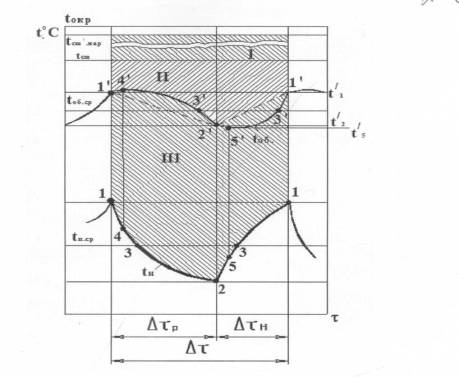
Рис.1 Изменение температур в циклично работающем
холодильнике:
![]() – температура поверхности испарителя, в момент запуска
компрессора;
– температура поверхности испарителя, в момент запуска
компрессора; ![]() – температура поверхности испарителя, в момент остановки
компрессора; 3– линия средняя за цикл температуры стенки испарителя
– температура поверхности испарителя, в момент остановки
компрессора; 3– линия средняя за цикл температуры стенки испарителя ![]() ;
; ![]() – средняя за цикл температура в камере,
– средняя за цикл температура в камере, ![]() ;
; ![]() -
- ![]() – дифференциал
замерзания;
– дифференциал
замерзания; ![]() -
- ![]() – диапазон запаздывания;
– диапазон запаздывания; ![]() – температура объекта соответствующая моменту пуска
компрессора;
– температура объекта соответствующая моменту пуска
компрессора; ![]() – температура объекта соответствующая моменту остановки
компрессора;
– температура объекта соответствующая моменту остановки
компрессора; ![]() – температура окружающей среды;
– температура окружающей среды; ![]() – температура охлаждаемого объекта;
– температура охлаждаемого объекта; ![]() – средняя температура охлаждаемого объекта;
– средняя температура охлаждаемого объекта; ![]() – средняя температура испарителя;
– средняя температура испарителя; ![]() – температура наружной стенки камеры;
– температура наружной стенки камеры; ![]() – температура внутренней стенки камеры;
– температура внутренней стенки камеры; ![]() – время работы холодильника;
– время работы холодильника; ![]() – время простоя холодильника;
– время простоя холодильника; ![]() – время цикла холодильника.
– время цикла холодильника.
Теплоприток через изоляционные
конструкции за время ![]() :
:
![]() , Вт. (1)
, Вт. (1)
Теплоприток ![]() от внутренних
поверхностей стен к камере за то же время:
от внутренних
поверхностей стен к камере за то же время:
![]() , Вт. (2)
, Вт. (2)
Тепло воспринимаемое испарителем:
![]() (3)
(3)
При интенсивной теплоотдаче от
поверхности компрессора окружающему воздуху и использовании предконденсатора с
частичной или полной конденсацией хладона для охлаждения масляной ванны
уравнения (2 и 3) принимают вид:
![]() , Вт (4)
, Вт (4)
![]() , Вт (5)
, Вт (5)
Тепловой баланс камеры определяется
уравнением:
![]() , (6)
, (6)
а общий перепад температур делится в
следующей пропорции:
![]() (7)
(7)
В нестационарном процессе при
цикличной работе холодильной машины тепловой баланс камеры может быть составлен
в дифференциальной форме:
![]() ,
(8)
,
(8)
отсюда
![]() (9)
(9)
Левая часть уравнения становится
равной нулю, а температура ![]() проходит через эксцентрум
в момент, когда удовлетворяется уравнение, подобное уравнению (7), в котором
вместо средних значений температур
проходит через эксцентрум
в момент, когда удовлетворяется уравнение, подобное уравнению (7), в котором
вместо средних значений температур ![]() и
и ![]() подставляют их
текущие значения
подставляют их
текущие значения ![]() и
и ![]() .
.
Аналогично
в варианте холодильного агрегата с вынесенными за пределы помещения
компрессионно – конденсаторным блоком и наличии предконденсатора, уравнение (9) имеет вид:
![]() (10)
(10)
По
знаку второй производной определяем вид экстремума. Легко показать, что в
рабочую часть цикла, когда![]() , температура
, температура ![]() проходит через
максимум, а в нерабочую часть цикла, в которой
проходит через
максимум, а в нерабочую часть цикла, в которой ![]() –через минимум.
–через минимум.
Обратимся
к рис.1. в момент пуска компрессора (точка 1) температура ![]() высока, а разность
высока, а разность ![]() меньше, чем следует
из равенства (8), поэтому температура камеры
продолжается повышаться. В точке 4, в которой
меньше, чем следует
из равенства (8), поэтому температура камеры
продолжается повышаться. В точке 4, в которой ![]() удостоверяет
равенству (7), температура
удостоверяет
равенству (7), температура![]() проходит через
экстремум (максимум), после чего начинает снижаться все более ускоренно.
проходит через
экстремум (максимум), после чего начинает снижаться все более ускоренно.
В момент
остановки компрессора (точка 2) разность ![]() имеет наибольшее
значение, поэтому
имеет наибольшее
значение, поэтому ![]() продолжает снижаться
даже после остановки компрессора и последующего повышения
продолжает снижаться
даже после остановки компрессора и последующего повышения ![]() . Только в точке 5 снова удовлетворяет равенству (10) и температура
. Только в точке 5 снова удовлетворяет равенству (10) и температура
![]() снова проходит через
экстремум (минимум) и затем начинает повышаться все более ускоренно.
снова проходит через
экстремум (минимум) и затем начинает повышаться все более ускоренно.
Поскольку
в реальных условиях температура стенки и водяной эквивалент непостоянны, то
амплитуда колебаний температуры камеры ![]() всегда больше
разности температур
всегда больше
разности температур ![]() в моменты пуска и
остановки компрессора.
в моменты пуска и
остановки компрессора.
Переменная
знака изменения ![]() происходит не в
точках 1' и 2' а позднее, в точках
происходит не в
точках 1' и 2' а позднее, в точках ![]() в которых
производная
в которых
производная ![]() равна нулю, а
разность
равна нулю, а
разность ![]() имеет определенное
значение.
имеет определенное
значение.
В точках 1' и 2' происходит смена закона
изменения протекания ![]() , следовательно, и смена
закона изменения разности
, следовательно, и смена
закона изменения разности ![]() количества тепла,
отводимого испарителем.
количества тепла,
отводимого испарителем.
В
зависимости от требований, предъявляемых к точности расчёта, возможно принятие
одного из трех предположений, относящихся к температуре объекта, а именно:
А) неизменность температуры ![]() ;
;
Б) изменение её по отрезкам прямых ![]() и
и ![]() (на рисунке показаны пунктиром);
(на рисунке показаны пунктиром);
В) изменение по действительной
кривой ![]() .
.
Для улучшения метода расчета необходимо
создание общей математической модели холодильника, состоящего из шкафа и
холодильного агрегата. Эта модель должна включать в себя описание элементов,
недостаточно исследованных в настоящее время, например, циклично работающего
компрессора, нестационарной теплопроводности ограждений шкафа, а также
устранить упрощения, неизбежные при нынешнем состоянии методики расчетов.
Математическая модель, показывающая, как изменяются параметры в отдельных
точках и в холодильнике в целом при изменении двух основных независимых
переменных – температуры окружающего воздуха и установки терморегулятора, –
должна соответствовать конкретному типу холодильника: а) с одним испарителем, б)
двухкамерному с принудительной циркуляцией воздуха и т. п.
Разработка методики анализа
колебаний температуры в камере холодильника имеет большое значение в вопросах
проектирования, когда уже на этой стадии можно закладывать принципиально новые
технические решения, приводящие к снижению колебаний температур и достижению
требуемых значений в соответствии с ГОСТ 16317 – 87 нижнего уровня температур в
относительно короткие сроки, приводящие к снижению усушки продуктов при их
хранении и, соответственно снижению энергопотребления.
Литература
1.
Лёвкин В.В. Теоретические основы
расчёта характеристик цикличной работы бытовых холодильных приборов
компрессионного типа / Лёвкин В.В., Гамзаян А.Ю., Блатман Г.М., Харламова С.П. //Изв.
вузов. Сев.–кавк.р Техн. науки.– 2006. Прил. №1.–с.90-94.
2.
Темлотехника/ В.Н. Луканин, М.Г.
Шатров, Г.М. Камфар и др.; под ред. В.Н. Луканина. –2-е изд.–М: Высш. ш., 2000.
671с.