Магистр
математики, магистр менеджмента Омарова М.Т.
Магистр экономических наук Тынгишева А.М.
Карагандинский экономический университет Казпотребсоюза
Применение
принципа оптимальности Беллмана для решения задач динамического
программирования
В последнее время особое развитие получили методы
оптимального управления в задачах экономики, т.к. основной причиной такого
процесса является все большее удорожание средств для решения задач управления и
реализации полученных результатов. Оптимальным управлением называется выбор
наилучшего среди множества всевозможных вариантов управления [1, стр. 39].
Динамическое программирование является одной из
разновидностью подхода оптимизации в задачах математического программирования.
Отличительной особенностью решения оптимизационных задач динамического
программирования является сведение его к решению более простых «подзадач» и
оптимизации целевой функции на каждом этапе. Поэтому нахождение оптимального
решения (максимума или минимума функции) является задачей динамического программирования.
Эта функция характеризует состояние системы, которая всегда меняется, при этом проходя
этапы своего развития. Динамическое программирование позволяет выбор управления
переходом от одного этапа к другому таким образом, чтобы на самом последнем этапе
получить оптимум данной функции [2, стр. 57].
Таким образом, можно ввести следующее
определение:
– динамическое программирование – это метод
оптимизации, приспособленный к операциям, в которых процесс принятия решения
может быть разбит на этапы (шаги). Такие операции называют многошаговыми [3, стр.
245].
Динамическое программирование дает возможность
привести одну сложнейшую задачу с несколькими переменными ко многим задачам с
маленьким количеством переменных, ускоряя процесс принятия управленческого
решения и сокращая при этом время на принятие решения.
Во
многих задачах и примерах, которые решаются данным методом, в процессе
управления, как мы говорили ранее, происходит разбиение на некоторые шаги. Шагом
можно считать, например, какой-то период времени, если мы распределяем ресурсы
производственной деятельности на несколько лет. В другом же случае шагом будет,
например, номер каждого предприятия, если будет распределение между этими
предприятиями определенных средств. В некоторых же других задачах может
вводиться искусственно разбивка на шаги. Например, процесс управления
происходит непрерывно, и в то же время мы можем его представить в виде
дискретного процесса, при этом разбивая условно этот процесс на определенные
отрезки (шаги). Для конкретных условий задачи при этом нужно правильно выбирать
длину каждого шага таким образом, чтобы было получено более простая задача по
оптимизации на каждом конкретном шаге задачи и обеспечивать при этом
необходимую точность вычислений [4, стр. 364].
Рассмотрим пример эффективного распределения
банкоматов между филиалами банка методом динамического программирования.
Задача 1. Руководство коммерческого банка г.
Караганды считает целесообразным распределение 5 банкоматов между тремя
филиалами, находящимися в городах Абай, Каркаралинск и Жезказган, и планирует
получить за неделю максимальный доход (млн. тг) от их совместного
использования. Функции дохода, в зависимости от применяемого количества
банкоматов в каждом из трех филиалов, приведены в таблице исходных условий (см.
таблицу 1).
Таблица 1
|
Доход по филиалам банка |
Количество банкоматов, Х |
|||||
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
g1(X) |
0 |
0,21 |
0,33 |
0,45 |
0,54 |
0,66 |
|
g2(X) |
0 |
0,20 |
0,34 |
0,39 |
0,55 |
0,6 |
|
g3(X) |
0 |
0,19 |
0,39 |
0,41 |
0,53 |
0,64 |
Математическая модель
задачи
Определить 
Решение:
На основе рекуррентного уравнения Р. Беллмана
рассчитываем значения функций по шагам для 
, 
, 
, изменяя х1,
х2 и х3 от 0 до 5.
1-ый этап. Решение для 
очевидное, т.е.
. Заносим эти значения в новую таблицу (см. таблицу
решения).
2-ой этап. Решение уравнения для 
:
В эту формулу подставим вместо Х значения 1, 2,
3, 4, 5.
При Х=1
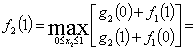
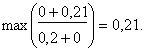
Нужно
обратить внимание на то, что значение 0,21
было получено при сумме 
и 
, т.е. при х2=0. Запишем значения 
и х2 в таблицу решения.
При Х=2
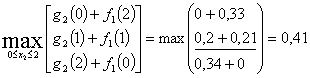при х2=1.
Запишем значения 
и х2 в таблицу решения.
При Х=3
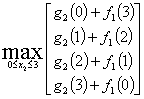
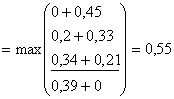при х2=2. Запишем значения 
и х2 в таблицу решения.
При Х=4
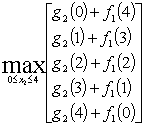
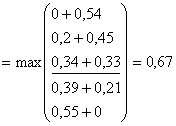при х2=2. Запишем значения 
и х2 в таблицу решения.
При Х=5
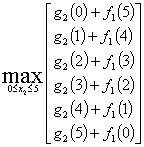
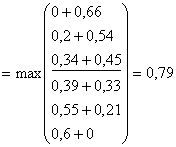при х2=2. Запишем значения 
и х2 в таблицу решения.
3-ий этап. Решение уравнения для 
:
В эту формулу подставим вместо Х значения 1, 2,
3, 4, 5. Получим:
При Х=1
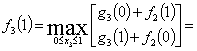
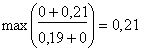при х3=0. Запишем значения 
и х3 в таблицу решения.
При Х=2
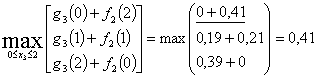при х3=0. Запишем значения 
и х3 в таблицу решения.
При Х=3
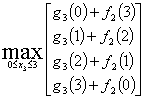
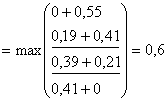при х3=1;2. Запишем значения 
и х3 в таблицу решения.
При Х=4
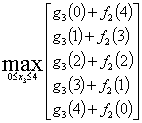
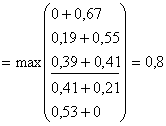при х3=2. Запишем значения 
и х3 в таблицу решения.
При Х=5
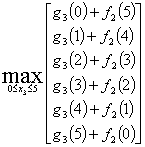
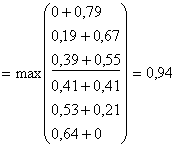при х3=2. Запишем значения 
и х3 в таблицу решения (см.
таблицу 2).
Таблица 2
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
0 |
0,21 |
0,33 |
0,45 |
0,54 |
0,66 |
|
Х1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
0 |
0,21 |
0,41 |
0,55 |
0,67 |
0,79 |
|
Х2 |
0 |
0 |
1 |
2 |
2 |
2 |
|
|
0 |
0,21 |
0,41 |
0,6 |
0,8 |
0,94 |
|
Х3 |
|
0 |
0 |
1, 2 |
2 |
2 |
|
Составлено
авторами на основе расчетных показателей задачи 1 с учетом данных таблицы 1 |
||||||
Анализ решения
Максимальное значение функции цели (доход) 
при х3=2.
Это значит, в третьем филиале необходимо установить 2 банкомата.
Тогда на остальные два филиала остается 5 – 2 = 3 банкомата. Значение дохода 
. При этом во 2-ом филиале следует установить 2
банкомата.
Следовательно, на 1-ый филиал остается 3 – 2 = 1 банкомат. При этом доход равен
0,21.
Таким образом, руководству банка необходимо
принять следующее оптимальное решение:
– в 1-ом филиале разместить 1 банкомат, доход от
него равен 0,21 млн. тг;
– во 2-ом филиале – 2 банкомата, доход от него
равен 0,34 млн. тг;
– в 3-ем филиале – 2 банкомата, доход от него
равен 0,39 млн. тг.
Суммарный доход от совместной работы 5-ти
банкоматов будет равен 0,21+0,34+0,39=0,94 млн. тг за неделю.
Теперь проведем анализ задачи по оптимальному
распределению инвестиций между дочерними компаниями предприятия методом
динамического программирования.
Задача 2. Общее собрание акционеров
промышленного предприятия выдвинуло предложение по наращиванию производственных
мощностей с целью увеличения выпуска однородной продукции дочерним компаниям,
принадлежащим данному предприятию.
Для реализации данной задачи собрание акционеров
поручило выделить средства в объеме 200 млн. тенге с дискретностью 50 млн.
тенге, причем в одну компанию можно осуществить только одно вложение. Следует
отметить, что прирост выпуска продукции в дочерних компаниях зависит от
выделенной суммы, и эти значения представлены компаниями предприятия и
содержатся в таблице исходных условий (смотрите таблицу 3).
Таблица 3
|
Инвестиции, х млн. тенге |
Прирост выпуска продукции, млн. тенге |
|||
|
Компания №1, |
Компания №2, |
Компания №3, |
Компания №4, |
|
|
50 100 150 200 |
25 60 100 140 |
30 70 90 122 |
36 64 95 130 |
28 56 110 142 |
Следует разработать план распределения
денежных средств между четырьмя дочерними компаниями предприятия, чтобы данный
план обеспечивал максимальный прирост выпуска продукции.
Решение:
Вначале разобьем решение задачи на 4 этапа по
количеству компаний, в которые предполагается осуществить инвестиции.
1-й этап. Для первой компании уравнение
Беллмана будет иметь вид 
.
Т.е. нвестиции производим только первой компании.
Тогда
2-й этап. Инвестиции выделяем
первой и второй компаниям. Рекуррентное соотношение для этого этапа имеет вид
Тогда 
при х=50
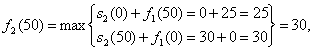
при х=100
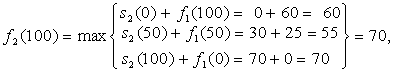
при х=150
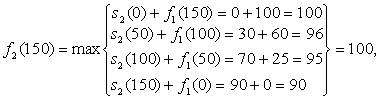
при х=200
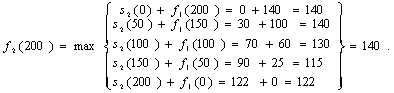
3-й этап. Финансируем 2-й этап и
третью компанию, тогда расчеты проводим по формуле
Получим
при х=50
при х=100
при х=150
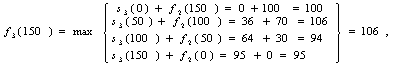
При х=200
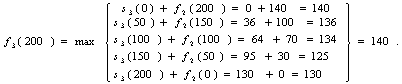
4-й этап. Инвестиции в объеме 200
млн. тенге распределяем между 3-м этапом и четвертой компанией.
Получим
при х=200
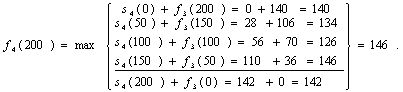
Возвращаемся от 4-го этапа к 1-му.
Максимальный прирост выпуска продукции в 146
млн. тенге получен на 4-м этапе как
.
Т.е. 110 млн. тенге соответствует выделению 150
млн. тенге 4-ой компании (это означает, что из данных 150 млн. тг используется
только 110 млн. тг).
Согласно 3-му этапу 36 млн. тенге получено следующим
образом:
.
Т.е. 36 млн. тенге соответствует выделению 50
млн. тенге третьей компании.
Согласно 2-му этапу 0 млн. тенге получено при выделении
0 млн. тенге 2-ой компании. Т.е. 
.
Таким образом, на основании данного решения
руководству предприятия необходимо распределить вложения в объеме 200 млн. тг между
четырьмя дочерними компаниями следующим образом:
- третьей – 36 млн. тенге;
- четвертой – 110 млн. тг (т.е. в первую и во
вторую компанию лучше не вкладывать инвестиции);
- неиспользованными средствами останутся 54 млн.
тг,
- прирост продукции будет максимальным и
составит 146 млн. тенге.
Список использованной
литературы:
1.
Экономико-математические методы и модели: учебник для бакалавров / А.М. Попов,
В.Н. Сотников; под ред. проф. А.М. Попова. – М.: Издательство Юрайт, 2011. –
479 с. – Серия; Бакалавр.
2.
Элементы исследования операций: учебное пособие / Е.Г. Давыдов. – М.: КНОРУС,
2013. – 158 с.
3.
Исследование операций в экономике: Учебное пособие для вузов / Н.Ш. Кремер,
Б.А. Бутко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: Банки
и биржи, ЮНИТИ, 1997. – 407 с.
4.
Математика в экономике: математические методы и модели: учебник для бакалавров
/ М.С. Чупрынов; под ред. М.С. Красса. – 2-ое изд., испр. и доп. – М.:
Издательство Юрайт, 2013. – 541 с. – Серия: Бакалавр. Базовый курс.