Математика/4. Прикладная математика

Батыров Б.Е., к.ф.-м.н., доцент

Северо-Казахстанский государтвенный университет им М. Козыбаева, Республика Казахстан

О группе подстановок

Известно, что теория групп является основным разделом общей алгебры. В математической литературе эта теория достаточно глубоко разработана. В учебниках по общей алгебре для студентов математических и технических специальностей наряду с описанием теории групп приводятся примеры групп [1]. В качестве основного множества в таких примерах рассматривались числовые множества с обычными операциями сложения или умножения. Изучаются и примеры, носящие прикладной характер. Одним из таких примеров является группа подстановок . Но в таких примерах редко рассматриваются их подробное доказательство.

Целью настоящей работы является изучение группы подстановок на примере множества .

Обозначим через множество, состоящее из первых натуральных чисел, т.е..

Подстановкой множества состоящего из  первых натуральных чисел, называется взаимно-однозначное отображение множества  на себя. Число  в этом случае называется порядком подстановки.

Подстановки будем записывать в виде таблицы, состоящей из двух строк и  столбцов следующим образом:

,

где – одно из чисел .

Композиция определяет операцию умножения на перестановках одного порядка.

Относительно этой операции множество подстановок порядка образует группу, которую называют симметрической и обычно обозначают через . Множество подстановок имеет вид:

.

, т.е. количество подстановок на множестве равно

Например, если , то .

.

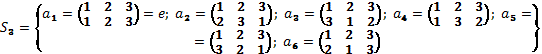Построим таблицу умножения для элементов множества .

Теперь вычисленные значения произведения элементов множества подстановок внесем в таблицу умножения элементов множества

Таблицы такого вида называют таблицей Кэли. Первая строка и первый столбец таблицы называются соответственно главной строкой и главным столбцом. Все элементы, находящиеся ниже главной строки и правее от главного столбца, представляет собой квадрат. Элементы, расположенные в каждой строке и в каждом столбце квадрата, разные. Такой квадрат называют латинским. Это означает, что введенная операция умножения подстановок замкнута на множестве .

В качестве примера группы покажем, что множество образует группу.

Теорема. Множество относительно умножения подстановок образует группу.

Доказательство. Проверим выполнимость условий определения группы.

1. Ассоциативность умножения подстановок из , т.е. равенство

следует из таблицы. Например, если , то

. (2)

Действительно, согласно таблице левая часть (2) имеет вид

. (3)

Теперь рассмотрим правую часть (2). По таблице видно, что

. (4)

Правые части равенств (3) и (4) равны между собой, тогда равны и их левые части.

2. Из первой строки и из первого столбца латинского квадрата видно, что существует элемент , что для любых

3. Для того, чтобы найти обратный элемент к данному элементу, берем элемент из главного столбца, далее идем по строке, где расположен рассматриваемый элемент, находим элемент на этой строке. Далее по столбцу, где расположен элемент , поднимаемся вверх по столбцу и элемент, стоящий по главной строке, является обратным элементом к данному элементу.

По этому алгоритму обратным элемент к элементу будет элемент . Таким образом, доказано, что множество образует группу.

Литература:

1. Кострикин А.И. Введение в алгебру. Основы алгебры. М.: МЦНМО, 2012.