Заурбекова Г.Н. -
магистрант
Казахский национальный университет имени
аль-Фараби, Алматы, Республика Казахстан
математическое
моделирование загрязнения
атмосферы нефтяной промышленностью
и анализ
результатов
Как известно, состояние атмосферного воздуха
играет огромный роль в воздействии на окружающую среду и здоровья человека.
Поэтому нахождение закономерностей распространения загрязняющих примесей в
атмосфере и их особенностей является важнейшей задачей в исследованиях процесса
загрязнения атмосферного воздуха. Решение данной проблемы представляет определенные трудности [1-10].
Для решения данной проблемы эффективно и экономически
выгодно необходимо использовать
математические методы исследования распространения вредных примесей в
атмосфере. Применение натурных, промышленных и полу промышленных исследовании
очень дорогие, а ставить эксперименты практически невозможно. Применение удачно
выбранной математической модели и численного алгоритма его решения достичь
желаемого результата. Предложенные нами
математические модели могут решить широкий класс задач, возникающих при
математическом моделировании загрязнения атмосферы с учетом свойств поверхности
земли и загрязнения воздушного бассейна.
Целью данной статьи является разработка оптимального
алгоритма и численной реализации данной проблемы. Известно, что метод
математического моделирования загрязнения атмосферы и переноса примесей дает
возможность проверки результатов моделирования в дальнейшем путем сопоставления
с фактическими данными.
Алгоритм моделирования распространения загрязняющих
примесей в атмосфере нефть и газодобывающего месторождения был реализован в
виде программы (рис. 1).
При этом необходимо учесть, что нами взяты следующие масштабы:
в системе 
– 2500 м х
2500 м х 200 м.
в системе
XYZ – 25 км х 25 км
х 0,2 км.
Входные информации, необходимые для математической
модели приведены в таблице 1.
ПРИЛОЖЕНИЕ D 1
Cx=55*m*k/(v/(1,4l+b+x)^2) Cy=Cx*s1 C=7,2*m*k/(v*l*(h+x)) S1=exp(-30*y^y/(1,4l+b+x)^2) Cx=1,3*m*k/v(0,6/(h*l)-42/(1,4l+b+x)^2) Cy=1,3*m*k/v(0,6/(h*l)-42/(1,4l+b+x)^2)*s1 C=2*m*k/(v*l*h)
Рисунок 1- Алгоритм в виде блок-схемы для реализации
на ЭВМ математической модели
загрязнения выбросами нижних слоев атмосферы
Итак, в таблице 1 приведены данные о высоте приземного
слоя h, которая рассчитывается в модели по формуле [1]:
, (1)
где
=
– вертикальная
составляющая скорости вращения Земли.
Таблица 1
– Высота приземного слоя,
рассчитанная по модели
|
№ варианта |
Т, °C |
Т, °C |
м/с |
Т, °C |
м |
h |
|
1 |
1 |
2 |
4 |
315 |
10 |
54,04 |
|
2 |
1 |
2 |
4 |
315 |
100 |
54,04 |
|
3 |
1 |
2 |
2 |
315 |
10 |
23,74 |
|
4 |
1 |
2 |
2 |
315 |
100 |
23,74 |
|
5 |
-1 |
15 |
6 |
45 |
10 |
102,98 |
|
6 |
-1 |
15 |
6 |
45 |
100 |
102,98 |
|
7 |
-1 |
15 |
3 |
45 |
10 |
54,79 |
|
8 |
-1 |
15 |
3 |
45 |
100 |
54,79 |
При расчете высоты приземного слоя h возникают множества проблем. Предложенная нами
методика позволяет рассчитывать
величину h по формуле (1), поэтому является одним из главных
преимуществ данной модели.
В следующих рисунках 2-6 предложены результаты
вычисленного в результате созданного нами программного продукта. Одним из
важнейших элементов загрязнения атмосферы, влияющих на здоровье населения,
является двуокиси серы 
, поэтому произведен расчет распределения по территории
месторождения, отмеченного контуром. Нами специально выделены три из девяти
групп источников, соответствующие своим истинным положениям. В карте местности
ось OY направлена на север, а ось
OX – на восток. Отмеченные номерами
изолиний соответствуют следующим значениям концентрации:
, (2)
где:
k – номер соответствующей изолинии; ПДК – предельно допустимые концентрации загрязняющих
веществ в атмосферном воздухе (
=0,05 мг/м
–
среднесуточная).
Анализ
результатов вычисления. Группа
рисунков (рисунки 2-6) изолинии реализует вариант с различными уровнями
наблюдения (
=10 м, 
=100 м). В верхних слоях атмосферы с увеличением высоты
увеличивается скорость ветра (см. рис. 5) и увеличивается размер вихрей,
обслуживающий турбулентный обмен, что приводит к большому распространению
загрязняющих примесей. Как уже указывалось, в силу поставленных условий
расчета, выделить изолинии уровня единиц ПДK нет возможности (уровень 7). Может вызвать удивление сравнение рисунков
2 и
4 для аналогичных условий (меняется только
скорость ветра, для рисунка 4 скорость ветра в 2 раза меньше) – размывание на рисунке 4 больше, чем на рисунке 2,
хотя ветер меньше. Но изучение истинного состояния проясняет ситуацию – группа важных по вкладу в загрязнения источников 4-6
в четыре раза увеличила свою эффективную высоту, что и послужило более
далекому распространению примесей.
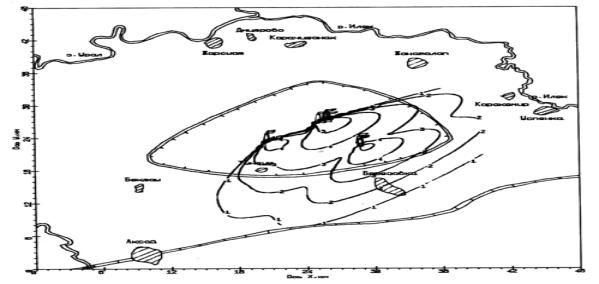
Рисунок 2 – Изолинии распределения концентрации СO2 на высоте 10 м.
Рисунок 3 – Изолинии распределения концентрации СO2 на высоте 100 м
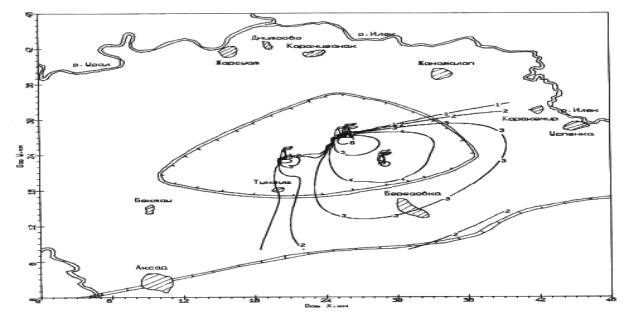Рисунок
4 – Изолинии распределения концентрации СO2 на высоте 10 м
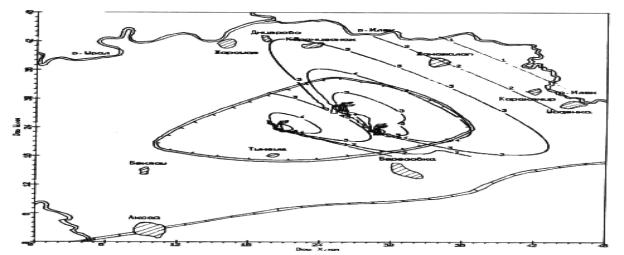Рисунок
9 – Изолинии распределения концентрации СO2 на высоте 100 м
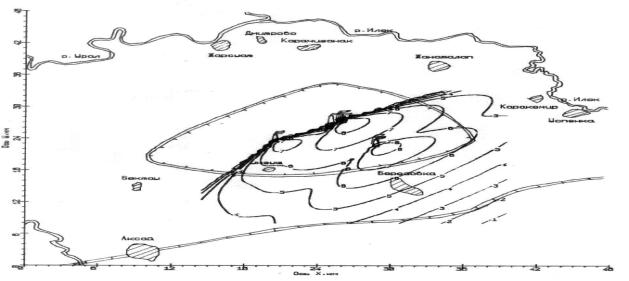Рисунок 10 – Изолинии распределения концентрации NO2 на высоте 10 м
Аналогичные рассуждения можно привести и к случаю
неустойчивой атмосферы (рис. 6).
Различие двух групп рисунков (устойчивой и неустойчивой атмосферы) обусловлено
более высоким подъемом и дальним переносом примеси в случае конвекции, что
приводит к более сжатым изолиниям в случае неустойчивой атмосферы на
высоте z=10 м и большим различием
на высоте z=100 м.
Литература
1.
Берлянд М.Е.
Современные проблемы атмосферной диффузии и загрязнения атмосферы. – Л.:
Гидрометеоиздат, 1975. – 448 с.
2.
Меллор Л.,
Херринг Х.Дж. Обзор моделей для замыкания уравнений осредненного турбулентного
течения // Ракетная техника и космонавтика.
– 1973. – (Т.11)№5. – С.17-29.
3.
Садоков В.П.,
Важник А.И. Предварительные результаты по методу прогноза осредненных
по времени полей метеоэлементов // Тез. докл. на Всесоюз. шк.-семинаре
по числен. моделированию крупномасштаб.
атмосфер. процессов и долгосроч. прогнозу погоды. – Дилижан, 1977.
4.
Оникул Р.И.,
Канчан Я.С. О расчетах загрязнения атмосферы от многих источников на ЭВМ с
применением унифицированных программ // Тр. ГГО. – Вып.467. – 1983. – С.41-49.
5.
Семевский Ф.Н.
К вопросу оценки глобального эффекта загрязнения среды инсектицидами // В кн.:
Проблемы экологического мониторинга и моделирования экосистем. – Л.:
Гидрометеоиздат. Т.7. – 1985. – С.288-292.
6.
Бурлибаев М.Ж.
Теоретические основы устойчивости экосистем трансзональных рек Казахстана:
дис... д-ра техн. наук: 25.00.27; 25.00.36 / Таразский гос. ун-т им.
М.Х.Дулати. - Тараз, 2004.
7.
А.А. Турсунов.
Гидроэкологические проблемы Республики Казахстан. – Издательский дом CA&CC Press. Швеция. 2010.– 213 с.
8.
М.Ж. Бурлибаев,
Р.К. Кайдарова, А.Н. Клец, Л.В. Лященко Концепция единой системы экологического
мониторинга// Гидрометеорология и экология. - 2000. - № 3-4. - С. 109-145.
9.
Айдосов А.А., Айдосова Г.А., Заурбеков
Н.С. Модельная оценка экологической обстановки
окружающей среды при аварийных ситуациях. - Алматы, 2010 (монография). – 414 с.
10.
Заурбеков Н.С. Модели
экологической обстановки окружающей среды при реальных атмосферных процессах. -
Алматы, 2010 (монография). – 368 с.