УДК 622.02+532.5
К.ф.-м.н. А.Г.Танирбергенов, к.т.н. Нурбекова,
магистрант Б.Ергалиев, магистрант Мураткажин Д.
Казахский национальный технический университет имени
К.И. Сатпаева
Алматы, Казахстан е-mail: tan.amanjol@mail.ru
ЧИСЛЕННЫЙ РАСЧЕТ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
СОЛЯНОКУПОЛЬНЫХ НЕФТЕГАЗОНОСНЫХ СТРУКТУР В ПРОЦЕССЕ ИХ РОСТА
Введение
Изучение условий формирования
солянокупольных структур и мантийных диапиров имеет
большое научное и практическое значение. С ними связано распределение месторождений полезных ископаемых в земной
коре. Кроме того, соляные структуры используются в качестве хранилищ
нефти и газа, а также «хранилищ-консервантов» термоядерных и других
промышленных отходов.
Исследование медленных
тектонических процессов проводится как правило, на базе модельных уравнений
ползущих течений Стокса в поле сил тяжести (гравитационная неустойчивость) с неизвестной заранее
эволюцией поверхности раздела сред. Начальная линейная стадия гравитационной
неустойчивости ползущего движения вязкой несжимаемой жидкости достаточно
подробно рассмотрена аналитическими методами [1] .
Наступающая
за начальной - нелинейная стадия мало изучена. Результаты, относящиеся к
некоторым задачам тектоники (преимущественно соляной), получены лабораторным и
численным моделированием. Однако экспериментальное
исследование не обеспечивает достаточного подобия реальным тектоническим
процессам.
Численное
моделирование формирования и развития соляных диапиров встречается с
определенными трудностями при описании раздела слоев и их эволюции, особенно в
развитой фазе. Подробная
библиография приведена в [2]. Расчеты проводились консервативно-разностными
методами с использованием монотонных разностных схем, либо методом
конечных элементов. Не обсуждая достоинства тех или иных методов, заметим, что
численное моделирование позволяет, детализировано оценить кинематические и силовые характеристики
течения, что экспериментальными методами затруднительно.
В настоящей работе проведен расчет напряженно-деформированного состояния
солянокупольных структур в процессе гравитационной неустойчивости и указываются возможные приложения этих
исследований в разведке, оценке и
разработке нефтегазовых месторождений.
Постановка задачи. Начально-краевая
задача, описывающая движение неоднородной сильновязкой несжимаемой жидкости в поле силы тяжести в
плоской постановке формулируется следующим образом. В прямоугольной области W требуется
определить вектор скорости ![]() давление
давление ![]() плотность
плотность ![]() динамическую вязкость
динамическую вязкость
![]() в момент времени
в момент времени ![]() удовлетворяющих
системе уравнений
удовлетворяющих
системе уравнений
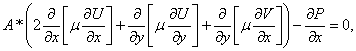 (1)
(1)
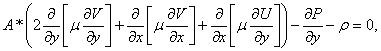 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
начальным и граничным
условиям
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Система уравнений (1) –(5), начальные и
граничные условия (6) –(8) записаны в безразмерном виде. Здесь ![]() соответственно
горизонтальная и вертикальная составляющие скорости.
соответственно
горизонтальная и вертикальная составляющие скорости. ![]() Система уравнений
(1)–(3) описывает движение неоднородной сильновязкой несжимаемой жидкости в
поле силы тяжести, т.е. течение Стокса, а уравнения (4), (5) учитывают сохранение плотности и
вязкости в любой момент времени. Коэффициент
Система уравнений
(1)–(3) описывает движение неоднородной сильновязкой несжимаемой жидкости в
поле силы тяжести, т.е. течение Стокса, а уравнения (4), (5) учитывают сохранение плотности и
вязкости в любой момент времени. Коэффициент ![]() равен отношению числа
Фруда к числу Рейнольдса,
равен отношению числа
Фруда к числу Рейнольдса, ![]() Здесь g – ускорение свободного падения,
Здесь g – ускорение свободного падения, ![]() характерные параметры среды, соответственно кинематическая вязкость, скорость и линейный размер области. В задачах гравитационной
неустойчивости отсутствует характерный масштаб скорости, поэтому в качестве
последнего в работе принимается вязкая
скорость
характерные параметры среды, соответственно кинематическая вязкость, скорость и линейный размер области. В задачах гравитационной
неустойчивости отсутствует характерный масштаб скорости, поэтому в качестве
последнего в работе принимается вязкая
скорость ![]() , где n – произвольное
число. Выбирая n определенным образом, получим
необходимый масштаб скорости рассматриваемой модели.
, где n – произвольное
число. Выбирая n определенным образом, получим
необходимый масштаб скорости рассматриваемой модели.
Численный
метод решения. Для численного решения
систем уравнений (1) –(3) используется итерационный процесс, основанный на
схеме расщепления по физическим процессам [3]. Пусть исследуемая область
течения Ω покрыта равномерной по x и y сеткой ячеек:
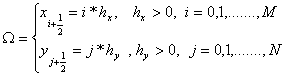
где
![]() размеры шагов сетки,
размеры шагов сетки, ![]() число ячеек сетки соответственно в направлениях x и y.
число ячеек сетки соответственно в направлениях x и y.
На первом этапе схемы расщепления по неявной схеме рассчитывается предварительное значение вектора
скорости:
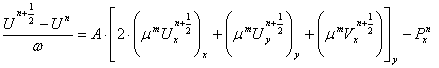 (9)
(9)
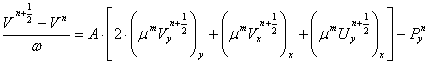 , (10)
, (10)
Уравнение
(9) рассматривается в точках сетки ![]() а уравнение (10) – в точках
а уравнение (10) – в точках ![]() . Для наглядности, например, член
. Для наглядности, например, член ![]() расписывается в
точках
расписывается в
точках ![]() следующим образом:
следующим образом:
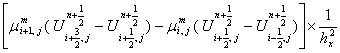 .
.
В уравнениях верхний индекс ![]() обозначает временной
слой, а
обозначает временной
слой, а ![]() номер итераций.
номер итераций.
На втором этапе по найденному промежуточному полю
скорости ![]() с учетом условия
соленоидальности вектора скорости
с учетом условия
соленоидальности вектора скорости ![]() находится поле
давления
находится поле
давления ![]() из уравнения:
из уравнения:
![]() . (11)
. (11)
Уравнение
(11) рассчитывается в точках ![]()
На третьем
этапе находим ![]() из уравнений:
из уравнений:
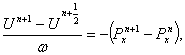 (12)
(12)
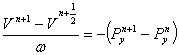 (13)
(13)
Уравнения
(12) и (13) рассматриваются соответственно в тех же точках, что и (9) и (10).
Для численного решения (4) и (5) используется консервативная схема
разности против потока [4], при этом шаг по времени ![]() выбирается с учетом
устойчивости и монотонности схемы:
выбирается с учетом
устойчивости и монотонности схемы:
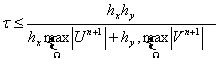 (14)
(14)
Для решения уравнений (9) – (10)
используется метод верхней релаксации. Как показали расчеты разностная схема (9)
– (13) абсолютно устойчива. Параметр ![]() выбирается с учетом
быстрой сходимости итерационного процесса.
выбирается с учетом
быстрой сходимости итерационного процесса.
Итак, предлагаемый алгоритм для
численного решения задачи (1)-(8)
выглядит следующим образом. Пусть ![]() известны (при
известны (при ![]() для
для ![]() и
и ![]() это будут начальные
данные ). Тогда неизвестные
это будут начальные
данные ). Тогда неизвестные ![]() определяются
итерационным процессом с повторением вышеуказанных трех этапов. При выполнении
условия
определяются
итерационным процессом с повторением вышеуказанных трех этапов. При выполнении
условия
![]()
итерационный
процесс заканчивается. Это и означает, что на ![]() - шаге по времени определены значения величин
- шаге по времени определены значения величин ![]() . Далее по явной схеме разности против потока вычисляются
неизвестные
. Далее по явной схеме разности против потока вычисляются
неизвестные ![]() на
на ![]() шаге по времени. Для нахождения
шаге по времени. Для нахождения ![]() опять применяется
итерационный процесс. Аналогично, определяются все величины
опять применяется
итерационный процесс. Аналогично, определяются все величины ![]() (
(![]() ) вплоть до необходимого
) вплоть до необходимого
![]() слоя по времени. Рассмотренный численный метод пригоден при
любых распределениях вязкости и плотности, характерных для осадочного чехла в
природных условиях.
слоя по времени. Рассмотренный численный метод пригоден при
любых распределениях вязкости и плотности, характерных для осадочного чехла в
природных условиях.
После расчета скоростей перемещений ![]() определяются напряжения
определяются напряжения ![]() по известным формулам
гидромеханики.
по известным формулам
гидромеханики.
Анализ
результатов расчета. На рисунках 1 и 2 показаны
изолинии нормальных ![]() ,
, ![]() и касательных напряжений
и касательных напряжений ![]() для двух различных безразмерных
моментов времени в процессе роста соляного купола. Из рисунков видно, что экстремумы напряжений концентрируются
вокруг соляного купола. Это надо учитывать при бурении и эксплуатации скважин,
например из-за роста соли, возможно,
смятие обсадных колонн нормальными и касательными напряжениями.
для двух различных безразмерных
моментов времени в процессе роста соляного купола. Из рисунков видно, что экстремумы напряжений концентрируются
вокруг соляного купола. Это надо учитывать при бурении и эксплуатации скважин,
например из-за роста соли, возможно,
смятие обсадных колонн нормальными и касательными напряжениями.
Начально-краевая
задача (1)-(8) корректна при обратном течение времени, т.е. можно восстановить
предысторию формирования куполов. Это даст дополнительную
геолого-морфологическую информацию, которая может быть использована в
геологоразведке [5]. Возможно, провести проводку эксплуатационных скважин с
наклонной криволинейной траекторией в обход слабопрочного соляного купола,
предотвращая прихват бурильных колонн [6].
Изолинии напряжения ![]()
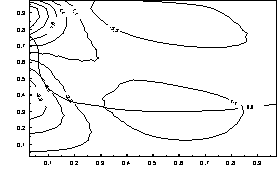
Изолинии напряжения ![]()
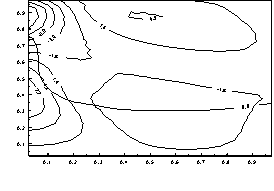
Изолинии напряжения ![]()
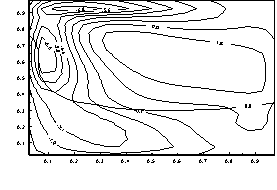
Рисунок 1 – Напряженно-деформированное состояние для момента
времени t=0.3. Параметры модели: ![]() ;
; ![]() .
.
Изолинии напряжения ![]()
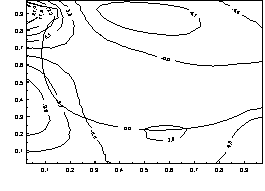
Изолинии напряжения ![]()
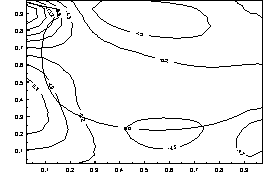
Изолинии напряжения ![]()
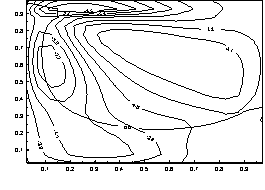
Рисунок
2 – Напряженно-деформированное состояние для момента времени t=0.5. Параметры
модели: ![]() ;
; ![]() .
.
. Заключение.
Рациональное использование распределения поля девиаторов напряжений позволит
оптимально вести как разведку, так и добычу углеводородов, с существенным снижением материальных
затрат. Сюда относятся задачи оптимального размещения нагнетательных скважин,
проведение гидравлического разрыва пласта, повышение коэффициента нефтеотдачи
пластов. Могут быть сформулированы задачи фильтрации и вытеснения, выработаны
меры по уменьшению смятия обсадных колон, с учетом неоднородного распределения
девиаторов напряжений. Наконец можно развить экологически безопасную технологию
строительства глубоких и сверхглубоких скважин в солянокупольных структурах[7].
Это не
полный перечень тех приложений компьютерного моделирования формирования соляных
диапиров, который, в конечном счете
приведет к эффективному повышению нефтеотдачи пластов.
Список литературы
1.
Ержанов Ж.С., Егоров
А.К., Гарагаш И.А., Искакбаев А., Коксалов К. Теория складкообразования в
земной коре. М: Наука, 1975, 239с.
2. Мартынов Н.И., Танирбергенов А.Г.
Численное моделирование формирования соляных диапиров в земной коре.
Математический журнал, 2006, т.6, №1, 67-73с.
3. Белоцерковский
О.М. Численное моделирование в механике сплошных сред. М.: Наука, 1984, 520с.
4.
Роуч Х. Вычислительная гидродинамика. М.: Мир, 1980, 616с.
5. Бекжанова Г.Р. Геология регионов Каспийского и Аральского морей. Алматы:
Изд. «КазГЕО», 2004, 472с.
6. Айталиев Ш.М., Кудайкулов А.К.,
Мардонов Б.М. Механика прихвата бурильных колонн в нефтегазовых скважинах.
Атырау-Алматы: Изд. «Эверо», 1999, 82с.
7. Хаиров Г.Б. Экологически безопасная
технология строительства глубоких разведочных скважин. М.: Изд. ВНИИОЭНГ, 1996,
204с.