К.т.н. Беляева А. Ю.
Национальный технический
университет Украины «Киевский политехнический институт»
Вибір принципу
розрахунку пружних елементів, що не можуть вважатися оболонками
Аналіз проблеми визначення напружено-деформованого стану
елементів конструкцій призвів до того, що при розрахунку деталей складної форми
аналітичних методів не знайдено, тому необхідно використовувати чисельні
методи. Методи визначення напружено-деформованого стану мають задовольняти
наступним вимогам: забезпечувати необхідну точність, бути стійкими та достатньо
універсальними, мати можливість комп’ютерної реалізації [1].
На
даний різцетримач з пружним елементом у вигляді кільцевої пластини був
отриманий нами патент [4], однак, його ще не розраховували аналітично.
Метою
цієї статті є вирішення питання аналітичного розрахунку «нестандартної оболонки» чи конструкції
складної форми, як збірної конструкції. Це рішення пропонується для різцетримача з пружним елементом у вигляді
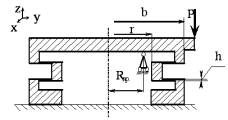
кільцевої пружини, що показана на рис. 1 [4].
Так
як конструкція, що показана на рис. 1, не може бути розрахована як оболонка,
будемо розглядати її у вигляді збірної конструкції з суцільних та кільцевих
пластин при визначених граничних умовах. Розрахуємо спочатку суцільну пластину
методом початкових параметрів.
|
|
|
|
Рис.
1. Розрахункова схема кільцевого пружного елементу: b – зовнішній ра-діус кільцевої пластини; r – внутріш-ній радіус кільцевої
пластини; Rпр – відстань від осі до шарніру; h – товщина кільцевої
пластини |
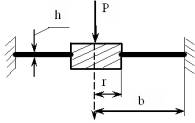
Рис.
2. Розрахункова схема наван-таження кільцевої пластини пружного елементу: r –
внутрішній радіус; b
– зовнішній радіус; h – товщина пластини |
Розглянемо
круглу суцільну пластину з зовнішнім радіусом b, на яку діє зосереджена сила Р
(див. рис.2). Будемо рахувати, що пластина жорстко закріплена по
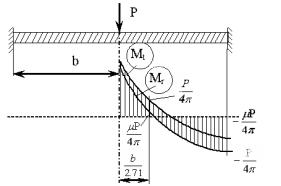
зовнішньому контуру. Побудуємо епюри моментів (рис. 3).
Інтенсивність поперечної сили в
даному випадку 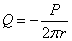 .
.
Користуючись диференційним
рівнянням другого порядку відносно функції ![]() :
: ![]()
Отримаємо 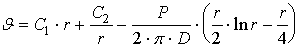 ,
,
де ![]() - функція, r - радіус пластини,
- функція, r - радіус пластини, ![]() - циліндрична
жорсткість, Е – коефіцієнт пружності,
- циліндрична
жорсткість, Е – коефіцієнт пружності,
![]() - коефіцієнт Пуансона,
h - товщина пластини.
- коефіцієнт Пуансона,
h - товщина пластини.
|
Рис. 3. Епюри
моментів круглої пластини |
Для того щоб усунути логарифм розмірної величини, додамо та віднімемо з
того рівняння добуток Тоді
функція |
![]()
Останні
доданки, які містять r в першій
степені, можна відкинути, так як це вплине лише на величину постійної ![]() , тоді
, тоді ![]()
додаткові
граничні умови
для ![]() , а саме:
, а саме: ![]() при
при ![]()
![]() та
та ![]() , де
, де ![]() - вісь-радіус
полярної системи координат, дозволяють постійну C2
прийняти рівною нулю, так як пластина безперервна (не кільцева). Для визначення
постійної C1 необхідно
використовувати граничну умову на зовнішньому краю пластини:
- вісь-радіус
полярної системи координат, дозволяють постійну C2
прийняти рівною нулю, так як пластина безперервна (не кільцева). Для визначення
постійної C1 необхідно
використовувати граничну умову на зовнішньому краю пластини: ![]() при
при ![]() .
.
З цієї умови
випливає ![]() та функція
та функція ![]() прийме вигляд:
прийме вигляд: ![]()
Напишемо
ще вираз згинальних моментів:
![]()
![]()
Епюри
моментів приведені на рис. 3.
При
![]() згинальні моменти
прагнуть до нескінченності. Для центральної частини пластини, однак, наведене
рішення не є слушним. Це пояснюється тим, що сила
згинальні моменти
прагнуть до нескінченності. Для центральної частини пластини, однак, наведене
рішення не є слушним. Це пояснюється тим, що сила ![]() , фактично, не може бути прикладена в одній точці, а завжди
буває розподілена по деякій площині. Крім того, навколо центра пластини вихідні
гіпотези теорії тонких пластин грубо порушуються і тому сама теорія
застосовуватися не може.
, фактично, не може бути прикладена в одній точці, а завжди
буває розподілена по деякій площині. Крім того, навколо центра пластини вихідні
гіпотези теорії тонких пластин грубо порушуються і тому сама теорія
застосовуватися не може.
Із
викладеного випливає, що наведене рішення годиться лише на деякому віддаленні
від центру (при ![]() ).
).
|
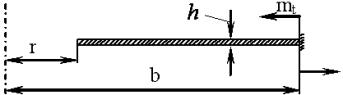
Рис. 4. Схема
навантаження кільцевої пластини: r
– внутрішній радіус; b
– зовнішній радіус, |
Наступним етапом
буде розраху-нок кільцевої пластини, жорстко закріпленої по зовнішньому конту-ру з
прикладеним по зовнішньому краю моментом (рис.4). |
Обчислимо
напруження та максимальний прогин круглої кільцевої пластини з жорстким
закріпленням по зовнішньому контуру. При ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Так,
як внутрішній край не закріплений, то ![]() , а зовнішній край жорстко закріплений -
, а зовнішній край жорстко закріплений - ![]() ().
().
Тоді ![]() ;
;
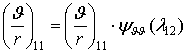 ;
; ![]()
![]()
Обчислимо прогин
пластини: ![]()
На основі розроблених розрахункових схем та основних
принципів розрахунку статичних та динамічних характеристик пружної зони
різцетримача рекомендовано використання аналітичних методів через недостатню їх
точність тільки для попередніх розрахунків, або для простих за конфігурацією
пружних елементів. Для точних розрахунків різцетримачів з пружними елементами
різної просторової конфігурації доцільно використати метод скінченних елементів.
Література
2.
Агапов В.П.
Метод конечных элементов в статике, динамике и устойчивости пространственных
тонкостенных подкрепленных конструкций./ В.П. Агапов Учебное
пособие / М.: Изд. АСВ, 2000. — 152 с.
4.
Патент
№ 56855А Украины. МПК В23В25/02.
Резцедержатель / Шевченко А.В., Беляева А.Ю.; заявитель и собственник
патента Национальный технический университет Украины "Киевский
политехнический институт". - № 2002107875; заявл. 03.10.2002; опубл. 15.05.2003
Бюл. № 5.