Технические науки/2. Механика

Д.т.н. Бешенков С.Н.

Смоленский филиал ФГБОУ ВПО «Московский государственный университет путей сообщения», Россия

к.ф.-м.н. Березняк И.С., к.т.н. В.И. Бешенкова

Смоленский филиал ФГБОУ ВПО «РЭУ им. Г.В. Плеханова, Россия

Нестационарное деформирование элементов конструкций с упругими связями, разносопротивляющимися растяжению и сжатию.

При анализе колебаний тонкостенных элементов конструкций с упругими связями обычно предполагается, что последние, в частности, упругое основание, одинаково сопротивляются растяжению и сжатию. Так как указанное условие выполняется не всегда, то возникает необходимость учета этого различия и его влияния на характеристики напряженно-деформированного состояния конструкции. Например, при анализе колебаний плит, панелей и трубопроводов, взаимодействующих с грунтами или контактирующих с упругими опорами и подкреплениями, препятствующими перемещениям только в одном направлении, в задачах их кавитационного взаимодействия с жидкостью или отрывного друг с другом.

В данной работе рассматриваются два подхода к решению подобных задач, излагаемые на примере нестационарных осесимметричных колебаний круговой пластины, контактирующей по части своей поверхности с безынерционным основанием с различными коэффициентами жесткости и на растяжение и сжатие.

Процесс её деформирования при действии возбуждающей нагрузки описывается дифференциальным уравнением [1]

; (1)

,

в котором -прогиб пластины с параметрами ; -реакция основания, связанная с прогибом соотношениями

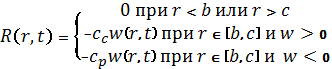(2)

Решение уравнения (1) ищем в виде ряда по собственным формам колебаний пластины , соответствующим заданным условиям закрепления контура.

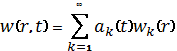. (3)

Аналогичным рядом представим правую часть (1), причем для неизвестной реакции примем кусочно-линейную аппроксимацию, разбив отрезок на частей. В результате приходим к уравнению для отыскания коэффициентов

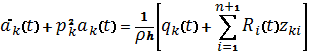; (4)

; ;

.

Здесь – реакция основания при , – квадраты собственных частот колебаний пластины.

Решение уравнения (4) при нулевых начальных условиях имеет вид

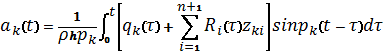(5)

Принимая для неизвестных функций кусочно-постоянную аппроксимацию, находим значения коэффициентов в момент времени

;

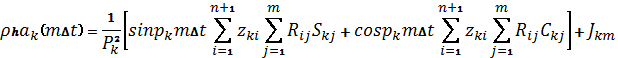; (6)

; .

Здесь - значение функции на -ом интервале времени.

Предполагая интервал времени достаточно малым, будем определять неизвестные величины -по значениям перемещений в соответствующих точках пластины в предыдущий момент времени

, (7)

где

Таким образом, алгоритм решения задачи состоит в следующем.

1. Исходя из нулевых начальных условий принимаем и по формуле (6) находим значения коэффициентов в момент времени .

2. Вычисляем значения прогиба в различных точках пластины в этот момент времени.

3. По формуле (7) находим значения реакции основания в точках пластины в интервале времени от до .

4. Повторяем описанный процесс и так шаг за шагом проходим весь рассматриваемый интервал времени.

Второй способ решения рассматриваемой задачи состоит в конечно-разностном анализе уравнения (1).

Разобъем пластину на N колец шириной . Используя явную трехслойную схему с центрально-разностной аппроксимацией производных [2], уравнение (1) во внутренних сечениях , запишем в виде

(); (8)

;

;

;

Значения в центре пластины () и в фиктивной точке () находим используя разностные аппроксимации условия , которые дают

; . (9)

Значения на контуре () и законтурной фиктивной точке () находим посредством конечно-разностной аппроксимации краевых условий.

Например, при защемлении контура (=0 при ), получаем

; (10)

Из нулевых начальных условий следует, что

; , (11)

поэтому на первом шаге по времени имеем

.

На рисунке 1 показаны рассчитанные двумя методами и практически совпадающие между собой зависимости от времени прогиба в центре защемленной по контуру стальной пластины радиусом м и толщиной м, возбуждаемой внезапно приложенной нагрузкой интенсивности и длительностью с. Кривые 1-3 соответствуют значениям , и коэффициентам жесткости 1) , ; 2) , 3) .

Из приведенных графиков видно, что форма движения точек пластины, взаимодействующей с основанием, разносопротивляющимся растяжению и сжатию, имеет асимметричный вид с преобладанием отклонений от недеформированного состояния в сторону, связанную с такой деформацией основания, сопротивление которой меньше. Время, в течение которого основание находится в сжатом и растянутом состоянии различно и зависит от соотношения между коэффициентами жесткости .

Чем больше различие между ними, тем ярче проявляются отмеченные особенности. Кроме того, после снятия нагрузки колебания пластины имеют несколько более высокочастотный характер при по сравнению со случаем при условии, что величина сохраняет одно и тоже значение.

Рис. 1 Зависимости от времени прогиба в центре пластины при различных значениях коэффициентов жесткости основания.

Литература

1. Колебания упругих систем. Т.1. 2-е изд., испр. и доп./Под ред. В.В. Болотина – М. Машиностроение, 1999 – 504 с.

2. Самарский А.А. Теория разностных схем – М.: Наука, 1983 – 616 с.