К.т.н.
Бондаренко Л.Н., к.т.н. Главацкий К.Ц., Брыльова М.Г., Сокол К.О.
Днепропетровский
национальный университет железнодорожного
транспорта
имени академика В. Лазаряна, Украина
Зависимость
мощности привода механизма передвижения мостового крана от положения тележки в
пролете и его влияние на износ реборд
Постановка проблемы.
Составляющая сопротивления от чистого качения кранового колеса по рельсу
предполагает прямую зависимость сопротивления от нагрузки. Поэтому, его
величина определяется из выражения:
,
где 
и 
- вес конструкции
и груза; 
- коэффициент
трения качения; 
- диаметр колеса.
Коэффициент трения качения
при этом принимается в зависимости от диаметра колеса и, например, при
диаметрах 400, 500, 560 и 630 мм его величина при скругленной головке рельса
равна 0,6 мм [1].
Отбрасывая
ошибочную теорию Рейнольдса о том, что главным источником сопротивления качению
является трение скольжения в месте контакта, отметим, что аналитическая
зависимость для определения коэффициента трения качения не могла быть получена
до решения Герцем в 1881-1881 г.г. задачи о контактных напряжениях и
деформациях.
После,
опираясь на решения Герца, Табор в 1955 г [2] получил эти зависимости от
полуширины пятна контакта и гистерезисных потерь. Однако, наличие в них
последних привело к невозможности их практического применения, поскольку
неизвестен способ их определения.
В [3]
получены экспериментально-аналитические зависимости, определяющие коэффициент
трения качения при точечном и линейном контактах, в которых коэффициент гистерезисных
потерь находится аналитически.
Цель работы
– найти величину статического и динамического сопротивления передвижению
мостового крана на прямолинейном участке пути в зависимости от положения
тележки в пролете и ее влияние на износ реборд с использованием аналитической
зависимости для определения коэффициента трения качения, зависящего от величины
полуширины пятна контакта между колесом и рельсом.
Основной
материал исследований. 1. Для решения первой задачи воспользуемся параметрами
крана, приведенными в [4]. Примем колесо цилиндрическим диаметром 
мм, рельс КР70 с радиусом закругления головки 
мм, диаметр цапфы
мм, приведенный
коэффициент трения подшипников 
(роликовые подшипники;
коэффициент, учитывающий трение реборд 
.
При схеме
касания «цилиндры со взаимно пересекающимися осями» полуширина пятна контакта в
случае равенства модулей упругости Е
материалов колеса и рельса и равенства коэффициента Пуассона 0,3 полуширина
пятна контакта согласно теории деформаций Герца [5]:
,
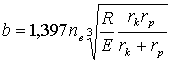(1)
где 
- прижимающая к
рельсу сила колеса; 
- коэффициент,
зависящий от соотношения коэффициентов уравнения эллипса касания, являющийся
функцией соотношения 
и равен 0,93.
Найдя
опорные реакции опор А и В в зависимости от положения тележки в
пролете найдем по формуле (1) полуширину пятна контакта и соответствующие ей
коэффициенты трения качения.
При
точечном контакте коэффициент трения качения определяется из выражения [3]: 
, (2)
где 
- в метрах.
Схема к
расчету нагрузок на ходовые колеса показана на рис. 1. В отличие от [4] здесь
вес кабины включен в вес тележки.
Отметим,
что полученная Табором формула, аналогичная (2), имеет вид:
,
(3)
где 
- коэффициент
гистерезисных потерь, и при 
м по (2) 
, т.е. можно считать, что экспонента здесь и представляет
. Приводимая в [6] формула 
представляет явно заниженню
величину и очевидно получена при малых радиусах или при недостаточных
деформациях.
Рис. 1. Схема к расчету нагрузок на
ходовые колеса: 1, 2, …, 7 – расчетные положения тележки
На рис. 2,
а и 2, б показаны зависимости от положения тележки в пролете (согласно рис. 1)
нагрузки на одно колесо опор А и В, а также соответствующие им
коэффициенты трения качения.
Из рис. 2,
б видно, что минимальная величина коэффициента трения качения соответствует
минимальному давлению колеса на рельс и равны 
мм, а
максимальная – максимальному давлению и равна 
мм при
рекомендуемой величине в случае 
мм, 
мм [1].
С учетом
этих значений 
и величинах
максимального давления колеса на рельс 
кН и минимального
кН сопротивление
чистому качению колеса опор А и В составит 
кН и 
кН.
Мощность
двигателей опор А и В с учетом трения в подшипниках составит: 
кВт;
кВт.
С учетом
трения реборд мощность двигателей опор А
и В составит:
кВт; 
кВт. Суммарная
мощность двигателей 
кВт. Статическая
мощность двигателей опор А и В: 
кВт.
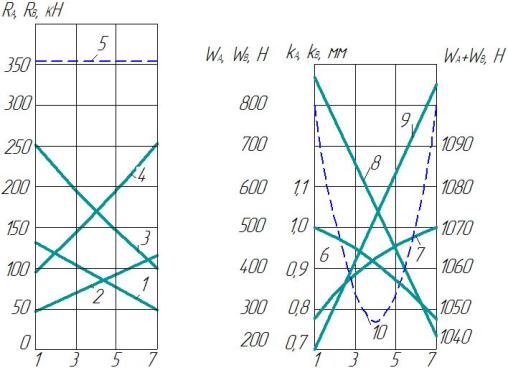
Рис. 2. Зависимости от положения
тележки в пролете (1, 2, 3,…, 7, рис. 1): 1, 2 – нагрузок на одно колесо опор А и В;
3, 4 – то же на два колеса; 5 – суммарная нагрузка (а); 6. 7 – коэффициенты
трения качения колес опор А и В; 8, 9 – сопротивление чистому качению
колес опор А и В; 10 – сопротивление передвижению крана от чистого качения
Если
тележка – в середине пролета, то 
кВт.
Согласно
нормативной методике статическая мощность двигателя 
кВт, а
динамическая (с учетом динамических нагрузок при пуске) 
кВт.
Динамическая
мощность выше полученных статических величин:
кВт, а 
кВт.
Таким
образом, нормативная величина мощности (из-за разности коэффициентов трения
качения) оказалась примерно на 20% меньше полученной по предлагаемому способу.
Из-за
разности мощностей двигателей опор А
(
кВт) и В (
кВт) возникает вопрос о влиянии этой разницы на износ
реборд.
2. Влияние
положения тележки мостового крана в пролете на износ реборд.
Профессор
Ковальский Б.С. [6]
считает, что коэффициент 
, учитывающий трение реборд, определяется из выражения:
,
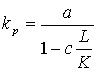(4)
где 
- при центральном
приводе и 
при раздельном
приводах; 
; 
- пролет; 
- база крана;
при, например, 
получим, что 
при центральном и
при раздельном
приводах.
Перекос
моста на рельсах влечет за собой трение реборд о рельсы, увеличение сопротивления
движению и расход энергии, сокращение срока службы колес и рельсов, появление
при движении толчков и ударов.
Исследованию
перекоса и «коэффициента реборд» [6], и способов его уменьшения посвящено много
работ, сводящихся, в основном, к минимуму разности диаметров ведущих колес,
уменьшению зазора между ребордами и рельсом или, наоборот, эти зазоры резко
увеличивали, но поиск рациональных решений не дал эффективных результатов и передвижение
кранов остается узким местом.
Считалось,
что применение конических колес решит проблему. Однако, дальнейшие исследования
показали, что более целесообразно применение раздельного привода при цилиндрических
колесах, не смотря на то, что мощность двигателей больше, чем при центральном
примерно на 20%.
Одной из
причин, а, возможно, и главной, является та, что мало внимания уделялось
теоретическим вопросам явления переноса и, в первую очередь, сопротивлению
качения колес по рельсам.
Составляющая
сопротивления от чистого качения кранового колеса по рельсу предполагает прямую
зависимость сопротивления от нагрузки. Поэтому, его величина определяется из
выражения:
.
Из рис. 2,
б видно, что минимальная величина коэффициента трения качения соответствует
минимальному давлению колеса на рельс и равна 
мм, а
максимальная – максимальному 
мм при
рекомендуемой величине для этого диаметра колеса (
мм) 
.
Для
равновесия моста разность максимальных сопротивлений 
должна
удерживаться силой Н, приложенной
перпендикулярно рельсу и расположенной на противоположном по диагонали колесе.
При колее L и базе В
условие равновесия:
,
(5)
откуда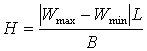 
. (6)
Отметим,
что эта формула получена независимо от формулы, предложенной ВНИИПИмаш [7],
которая имеет примерно такие же зависимости:
,
(6а)
где N – давление приводного колеса на рельс; 
- коэффициент
сцепления приводного колеса с рельсом; w – коэффициент
сопротивления движению.
Умножив
левую и правую части этого уравнения на коэффициент трения скольжения между
ребордой и рельсом, получим сопротивление трения реборд о рельс:
. (7)
Коэффициент, учитывающий
трение реборд:
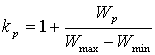. (8)
Величина 
может быть
получена и из формулы ВНИИПИмаш [8]:
.
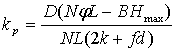(8а)
При 
кг и 
кг максимальная
величина 
при 
и 
при 
, а при густой смазке 
. Рекомендуется величина 
[5].
В
случае четырех колес и равномерного горизонтального давления между колесами и
рельсом 
и составляет 
Н, а 
Н.
В [6] для
безребордных колес величину нагрузки на ролик рекомендуется определять как 
, что составляет 14200 Н против 9547 Н.
На рис. 3
показана зависимость сопротивления качению опор А и В от положения тележки
в пролете с учетом трения подшипников и расчетная (8) величина коэффициента,
учитывающего трение реборд.
Как отмечалось выше, 
при центральном
приводе несколько ниже, чем при раздельном (1,48 и 1,60 соответственно)
несмотря на отсутствие забегания колес одной из сторон. И можно предположить,
что при центральном приводе основной причиной износа реборд являются толчки и
удары, а также процесс, близкий к автоколебаниям вследствие разного угла
закручивания вала. При полученных величинах сопротивлений опор А и В,
в зависимости от положения тележки в пролете, диаметре трансмиссионного вала
равном 50 мм углы закручивания отличаются на 10%, что при базе 
м дает поворот
колеса относительно вертикали на 0,440 и величина трения скольжения
при этом составляет 150 Н, что близко к величине сопротивления качению при
минимальной нагрузке на колесо.
Из формул
(7) и (8) видно, что при 
. Этого можно достичь за счет расположения груза на
середине пролета. Однако, это даст эффект только в период пуска, а в
дальнейшем, даже в этом положении груза, будут наблюдаться явления, аналогичные
центральному приводу.
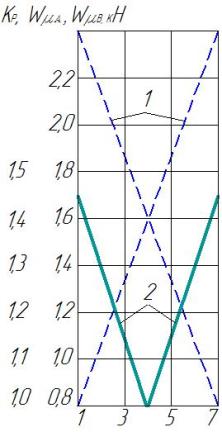
Рис. 3. Зависимость от положения
тележки в пролете (1, 3, 5, 7 – расчетные положения тележки): 1 – суммарного
значения сопротивления с учетом трения подшипников; 2 – коэффициента,
учитывающего трение реборд
Анализ
полученных формул и графиков позволяет сделать следующие выводы и
предложения:
– главной причиной появления скольжения реборд колес по
головке рельса является разность в сопротивлении от трения опор и величины
коэффициента трения скольжения между ребордой и рельсом;
– поскольку при центральном приводе коэффициент трения
реборд меньше, чем при раздельном примерно на 7…8%, то можно считать, что износ
реборд при расположении груза на середине пролета мостового крана будет на этот
же процент меньшим вследствие одинакового сопротивления движению опор;
– предлагаемый способ определения мощности двигателей
механизмов передвижения мостовых кранов предполагает использование классической
теории Герца по определению контактных деформаций и аналитической зависимости
Табора по определению коэффициента трения качения;
– мощность двигателей, полученная предлагаемым способом,
оказывается (для данного примера) на 20% выше, чем по существующим формулам;
– при тележке с грузом, расположенной в середине пролета,
мощность двигателей равна их суммарной величине при других положениях тележки,
поэтому мощность привода можно определить при положении тележки в середине пролета.
Литература
1.
Справочник по кранам: В 2 т. Т. 2 / Александров М.П.,
Гохберг М.М., Ковин А.А. и др. – Л.: Машиностроение, 1988. – 559 с.
2.
Джонсон К. Механика контактного взаимодействия. – М.:
Мир, 1989. – 510 с.
3.
Бондаренко
Л.М., Довбня М.П., Ловейкін В.С. Деформаційні опори в машинах. Дніпропетровськ:
Дніпро – VAL, 2002. 200 с.
4.
Иванченко Ф.К., Бондарев В.С., Колесник Н.П. и др.
Расчеты грузоподъемных и транспортирующих машин. – К.: Вища школа, 1975. – 520
с.
5.
Справочник по сопротивлению материалов /Писаренко Г.С.,
Яковлев А.П., Матвеев В.В. – К.: Наук. Думка, 1975. – 725 с.
6.
Ковальский Б.С. Вопросы передвижения мостовых кранов. –
Луганск: Изд-во ВНУ, 2000. – 63 с.
7.
Балашов В.В. Раздельный привод передвижения мостовых
кранов. – М.: ВНИИПИмаш, 1959. 36 с.
8.
Бондаренко Л.М., Главацький К.Ц. Відношення між тиском
реборд на рейку та коефіцієнтом опору руху і групою класифікації крана / Нові
матеріали в металургії та машинобудуванні // Зб. наук. праць ЗТТУ. - №1, 2001.
- С. 106-109.