Ìàòåìàòèêà/4. Ïðèêëàäíàÿ ìàòåìàòèêà
PhD Aipanov Sh.A.
Almaty Technological
University, Kazakhstan
Analytical solution
of controllability problem for linear systems
with use of
Gram-Schmidt orthogonalization procedure
The controllability problem for dynamic systems described by linear
differential equations is considered. The constructive method for building of a
set of all controls transferring the system from any initial state to any
desired final state in a finite time is proposed. To find the solution of the
problem the Gram-Schmidt orthogonalization procedure is used.
1.
Introduction
The mathematical control theory originated in
sixties of XXth century at present became one of thriftily developing in the qualitative
theory of differential equations. In particular, there were obtained the
necessary and sufficient conditions of existence of control, which transfers a
linear system from any initial state to any desired final state in a finite
time interval but at the same time the problem of building of a set of all such
controls is the actual one. In the given work the method of solution of
controllability problem for linear systems with use of Gram-Schmidt
orthogonalization procedure is proposed.
Models of systems with fixed trajectory endpoints (that is with assigned
initial and final states of the object) are widely used in solving of problems
of controllability and optimal control for air- and spacecrafts,
special-purpose robot handlers as well as electric, radio, economic, ecological
systems, etc.
Let us consider the linear system of the form
(1)
where 
are matrices with piecewise
continuous elements of dimensions 
, 
respectively; 
is the 
-vector of the object state; 
is the 
-vector of control. Let’s designate a solution of the system (1) through
, 
.
The system (1) is called completely controllable at time 
[2], if it can be transferred
from any initial state 
to the origin in a finite
time by properly selected control 
. Let 
be the set of those and only
those controls 
for which 
. Controllability problem for system (1) is in building of a set of
controls 
.
Let 
be the fundamental 
-matrix solution of linear homogenous differential equation 
, then transition matrix is equal to 
. As is known [3], system (1) shall be completely controllable at time 
iff
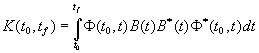(2)
(so
called controllability gramian) is a positively determined matrix for some time
value 
. Here symbol * means an operation of matrix transposition.
Further we propose that 
, that is 
. Designating columns of 
-matrix 
through 
, 
we obtain 
. Consequently, matrix (2) might be written in the form 
, where through 
are designated scalar
product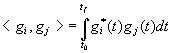s 
, 
. Thus, 
is a Gram determinant for
system of functions 
, being
, that is the given system is linearly independent.
As is known [3], control 
can be represented in the
form 
, where 
is a particular solution of
controllability problem for which the following equation
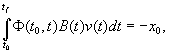(3)
is
valid and 
is any function from 
satisfying the condition
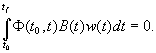(4)
Using
the above cited designations the integral equations (3), (4) can be written in
the form
(5)
(6)
where
through 
are designated components of
vector 
. In particular, equation (3) is valid for control [3]
(7)
and
function 
equal to zero almost everywhere on interval
satisfies equation (4). Set
of all solutions of equations (4) we designate through 
.
Thus, the controllability problem for system (1) leads to the necessity
of constructing of set W consisting
of functions 
that are orthogonal to the
system of linearly independent functions 
.
2. Construction of set W
Set of
functions 
can be built with use of
Gram-Schmidt [1] orthogonalization process. Let 
be an arbitrary function from 
. Let’s make orthogonalization of system of functions 
:
(8)
(9)
where 
, 
; 
, 
; 
as system of functions 
is linearly independent. For
obtained function 
exist equalities 
. From this using (8) we may receive (6). In particular, when system of
functions 
is linearly dependent we
obtain 
almost everywhere on interval
, in this case conditions (6) shall be also satisfied.
Thus, the general solution of controllability problem for system (1) may
be represented in the form 
, where 
is a particular solution of
controllability problem and 
is obtained by
orthogonalization of system of functions 
by formulas (8), (9), where 
is an arbitrary function from 
.
3. Example
Let’s
consider a linear system of the second order
(10)
for which 
, 
. It is required to transfer system (10) from any initial state 
, 
to a final state 
, 
in time interval 
.
Matrix 
may be found as
solution of differential equation 
satisfying initial
condition 
, where 
is an identity matrix. Substituting found
matrix 
into formula (2), we
calculate 
, that is the considered system (10) is completely controllable. Vectors
, 
, control (7) is of the form
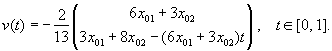(11)
Taking 
we make orthogonalization of
system of functions 
using formulas (8), (9). As
a result we obtain
(12)
Then the
control 
, where 
and 
are determined by formulas (11) and (12), transfers the system (10) from
initial state 
, 
to final state 
, 
in time interval 
.
Analogously, selecting various functions 
it is possible to obtain other
probable controls 
being a solution of
controllability problem for system (10).
4.
Conclusions
It is known that 
being a solution of
controllability problem for a linear system (1), is representable in the form
of a parallel shift of set 
to some vector 
, that is 
, where 
is a particular solution of
system of nonhomogeneous integral equations (5) and the set 
consists of all solutions of
system of homogeneous integral equations (6). In the given work the
constructive method for building of the set W
based on Gram-Schmidt orthogonalization procedure is proposed.
The controllability problem can be solved in much the same way also in
that case when it is necessary to transfer system (1) from any initial state 
to any final state 
in time interval 
. In this case instead (3) it is required to satisfy condition
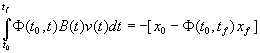(13)
and
condition (4) remains without change. As a particular solution of integral
equation (13) it is possible to take control [3]
In Appendix proofs of propositions about properties of sets 
and 
are given.
5. Appendix
Proposition 1. Let system (1) be completely controllable. Then the set 
consists of those and only those controls 
, which may be
represented in the form
,
(14)
where 
is some particular solution of nonhomogeneous
integral equation (3) and 
are arbitrary solutions of homogeneous integral
equation (4).
Proof. Let’s designate
through 
set of all functions
representable in the form (14). For arbitrary control 
solution of a differential
equation (1) has the form
.
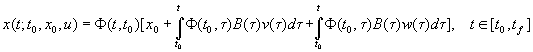As
functions 
and 
satisfy conditions (3) and (4)
respectively, we obtain 
. It means that 
, consequently, 
.
Further let’s choose some control 
and consider arbitrary
controls 
(set 
is not empty as system (1) is completely controllable). For these
controls the following relations shall be satisfied
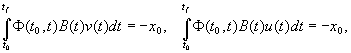(15)
as 
and 
. Let’s construct a function 
for which by virtue of (15) is valid (4). Thus,
any control 
may be represented in the
form (14), where functions 
and 
satisfy conditions (3) and (4)
respectively, consequently, 
.
From obtained relations 
and 
follows 
. £
Proposition 2. Let system (1) be completely controllable. Then the set 
of all solutions of
system of integral equations (6) consists of
those and only those functions 
, which may be represented
in the form (9), where 
is an arbitrary function from 
and functions 
are determined by formulas (8).
Proof. Let’s designate
through 
set of all functions
represented in the form (9). For arbitrary function 
equalities 
shall be satisfied. From this
using (8) equalities (6) may be obtained. Consequently, 
that means 
.
Relations (8) may be reduced to the
form
(16)
For
arbitrary functions 
we have 
. From this using equalities (16) may be obtained
. (17)
Let’s show that exists a function 
and it is such that 
may be represented in the
form (9). Let’s choose a function 
in the form
, (18)
where 
are arbitrary numbers. Substituting
(18) into (9) in regards with (17) we can assure in validity of relation (9). Consequently,
that means 
.
From obtained relations 
and 
follows 
. £
References:
1. Conway, A Course in Functional Analysis. New York: Springer, 1990.
2. R.E. Kalman, On the General Theory of Control Systems, in:
Proceedings of the 1st IFAC Congress, Vol. 1. London, Butterworths,1961,
pp. 481-492.
3. ß.Í. Ðîéòåíáåðã, Àâòîìàòè÷åñêîå
óïðàâëåíèå. Ì.: Íàóêà,1992.