Секция
“Математика”
подсекция №5
Фрактальные
окружности Вейерштрасса
Пенкин Ю.М., Белогорцева Л.Ю., Пенкин Д.Ю.
Национальный фармацевтический университет, г.Харьков
Харьковский национальный университет им. В.Н.Каразина
При математическом моделировании двумерных объектов, зачастую, возникает необходимость фрактального
представления их естественной формы. Для этого обычно используются традиционные
рекурсивные или итерационные методы фрактальной геометрии. Однако для
моделирования двумерных областей с фрактальными границами в некоторых случаях
успешно могут быть использованы обобщенные функции Вейерштрасса.
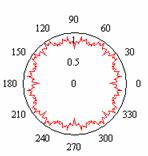
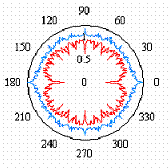
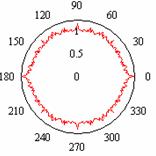
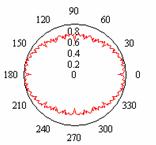
На рис.1 показаны примеры непрерывных
ломаных линий фрактальных окружностей, которые будем называть
окружностями Вейерштрасса, поскольку они определяются следующей угловой
зависимостью радиус-вектора:
![]()
где: ![]() -угловая координата;
-угловая координата; ![]() и
и ![]() -параметр масштабирования;
-параметр масштабирования;![]() -фрактальная размерность;
-фрактальная размерность; ![]() -нормирующий коэффициент;
-нормирующий коэффициент; ![]() -амплитуда фрактальной модуляции;
-амплитуда фрактальной модуляции; ![]() -обобщенные функции Вейерштрасса. Здесь и далее кривые на
рисунках представлены в полярной системе координат с масштабом прорисовки изображения
10. Параметр
-обобщенные функции Вейерштрасса. Здесь и далее кривые на
рисунках представлены в полярной системе координат с масштабом прорисовки изображения
10. Параметр ![]() выбран равным целым
значением для обеспечения периодичности функции
выбран равным целым
значением для обеспечения периодичности функции ![]()
![]() с периодом
с периодом![]() , что позволяет с помощью
периодической функции получить изображение одиночного объекта. Отметим,
что бесконечный ряд в этой формуле представляет собой обобщенную функцию
Вейерштрасса, которая является непрерывной функцией, но нигде не
дифференцируемой и фрактальной на всех масштабах
, что позволяет с помощью
периодической функции получить изображение одиночного объекта. Отметим,
что бесконечный ряд в этой формуле представляет собой обобщенную функцию
Вейерштрасса, которая является непрерывной функцией, но нигде не
дифференцируемой и фрактальной на всех масштабах ![]() >1.
>1.
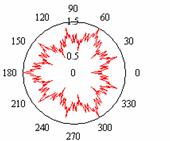
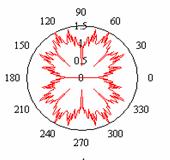
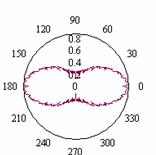
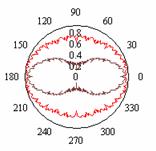
Варианты представления окружностей
с «односторонней» фрактальной модуляцией, которая определяется модулем функции
Вейерштрасса, показаны на рис.2а и рис.2б. На рис.2в показана возможность
представления области между двумя фрактальными границами с помощью комбинации
двух фрактальных окружностей. Введение в формулу для ![]() дополнительного
слагаемого
дополнительного
слагаемого![]() , где
, где![]() , позволяет представить области с эллиптическими фрактальными
границами, варианты которых показаны на рис.3. Отметим, что существующая
возможность секториального совмещения кривых
различных типов значительно расширяет границы моделирования форм двумерных
областей. Так в качестве примера, на рис.4 приведены некоторые модели форм
биологических объектов: на рис.4а:
, позволяет представить области с эллиптическими фрактальными
границами, варианты которых показаны на рис.3. Отметим, что существующая
возможность секториального совмещения кривых
различных типов значительно расширяет границы моделирования форм двумерных
областей. Так в качестве примера, на рис.4 приведены некоторые модели форм
биологических объектов: на рис.4а: ![]() при
при
![]() и
и ![]() при
при ![]() ; на рис.4б
; на рис.4б ![]() ; на рис.4в совмещены
; на рис.4в совмещены ![]() ;
; ![]() и
и ![]() .
.
а) ![]() б)
б) ![]() в)
в) ![]()
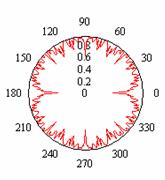 Рис.1
Фрактальные окружности Вейерштрасса.
Рис.1
Фрактальные окружности Вейерштрасса.
а) ![]() б)
б) ![]() в)
в) ![]() Рис.2
Варианты представление двумерных областей
Рис.2
Варианты представление двумерных областей
а)![]() б)
б)![]() в)
в)![]()
Рис.3 Варианты представление двумерных областей
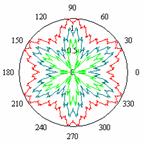
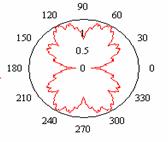
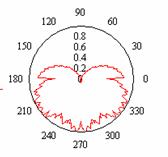
а)
«лист» б)
«бабочка» в)
«цветок»
Рис.4
Модели форм биологических объектов
Таким образом, на конкретных
примерах представлены широкие возможности моделирования двумерных областей с
фрактальными границами с помощью обобщенных функций Вейерштрасса.
Известно,
что определение фракталов включает свойство их самоподобия
(определение Мандельброта), согласно которому фракталы обладают свойством
масштабной инвариантности, или скейлингом, и
инвариантностью относительного параллельного переноса. Нетрудно убедится, что
при целых ![]() выполняется равенство
выполняется равенство ![]() , которое и определяет свойство секториального
скейлинга фрактальных окружностей Вейерштрасса.
Свойство периодичности функции является отражением инвариантности фрактальных
кривых относительно параллельного переноса (поворота).
, которое и определяет свойство секториального
скейлинга фрактальных окружностей Вейерштрасса.
Свойство периодичности функции является отражением инвариантности фрактальных
кривых относительно параллельного переноса (поворота).
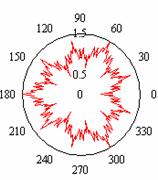
Проанализируем
пример, приняв радиус r=1 . На
рис.5а в полярных координатах представлена функция ![]() , где
, где ![]() , а масштаб «прорисовки» выбран 10 . Если выбрать
сектор
, а масштаб «прорисовки» выбран 10 . Если выбрать
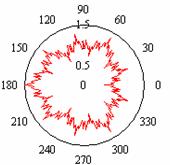
сектор ![]() и «развернуть» его до полной окружности, то мы получим функцию,
представленную на рис. 5б:
и «развернуть» его до полной окружности, то мы получим функцию,
представленную на рис. 5б: ![]() . Если выбрать сектор
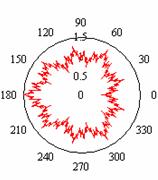
. Если выбрать сектор ![]() и развернуть его
также до полной окружности, то мы получим функцию, представленную на рис.5в:
и развернуть его
также до полной окружности, то мы получим функцию, представленную на рис.5в: ![]() . Видно, что при
выборе сектора
. Видно, что при
выборе сектора ![]() ,где m–целое число; и его развертывании до полной окружности
получаются подобные кривые, хотя из-за усечения
,где m–целое число; и его развертывании до полной окружности
получаются подобные кривые, хотя из-за усечения ![]() теряются некоторые
тонкие детали при их представлении.
Следует подчеркнуть, что анализируемые кривые являются не самоподобными, а самоаффинными, так как для координат r и
теряются некоторые
тонкие детали при их представлении.
Следует подчеркнуть, что анализируемые кривые являются не самоподобными, а самоаффинными, так как для координат r и ![]() используются различные масштабные множители.
используются различные масштабные множители.
а) ![]() б)
б) ![]() с)
с) ![]()
Рис.5 Скейлинговые свойства функции
![]() .
.
Таким
образом, можно утверждать, что фрактальные окружности Вейерштрасса обладают
свойством секториального скейлинга
при определенном выборе углового размера сектора, а именно ![]() ,где
,где ![]() –целое число. Отметим, что при
этом в качестве направления для границ
сектора может быть выбрано произвольное значение
–целое число. Отметим, что при
этом в качестве направления для границ
сектора может быть выбрано произвольное значение ![]() угловой координаты.
угловой координаты.
![]()