ЖОЙЫЛМАЛЫ ЭЛЛИПТІК ТҮРДЕГІ ТЕҢДЕУЛЕР ҮШІН ДИРИХЛЕ ЕСЕБІ СПЕКТРІНІҢ ДИСКРЕТТІЛІГІ

Дунбаева А., Берікбосын Ж.

Эллиптiк түрдегі теңдеулер стационарлық (тұрақты) процестердi, мысалы, денеде тұрақты температураның таралуы, өткiзгiштiң бетiндегi электр зарядтарының тепе-теңдiк күйi, сұйықтың потенциалды ағысы т.с.с. процестердi сипаттайды.

Эллиптiк түрдегі теңдеулер үшiн қойылған шеттiк есептердiң шешiмiн табу үшiн әртүрлi әдiстер қолданылады. Олардың iшiнде жиi қолданылатыны Фурье әдiсi, Грин функциясы әдiсi, интегралдық теңдеулер әдiсi т.б.

Эллиптік түрдегі операторларға қарағанда, жойылмалы эллиптік түрдегі операторлардың спектральды сұрақтары аз зерттелген. Бұл бағыттағы немесе осыған жақын жұмыстар М.М.Смирновтың, Х.Трибелдің, М.В.Келдыштың, П.Боллей және Т.Камюдің, О.А.Олейниктің, М. Отелбаевтың, Т.Ш.Кальменовтың, М.Б. Муратбековтың, Л.К.Кусаинова мен М.С.Айтенованың және басқа да ғалымдардың еңбектерінде кездеседі.

кеңістігінде төмендегі дифференциалдық операторды қарастырайық,

(1)

мұндағы W={(x,y): -p< x<p,0<y<1} тіктөртбұрыш.

(2.1) операторы - облысындағы у айнымалысы бойынша барлық ретті дифференциалдары анықталған функциялар жиынында берілсін және

(2)

(3)

шарттарын қанағтаттандырсын.

L операторының коэффициенттері төмендегі шарттарды қанағаттандырсын деп ұйғарайық:

- функциялары [0,1] кесіндісінде бөлікті үзіліссіз;

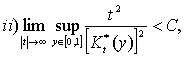мұндағы С>0 – кейбір бағаланған сан және [12] теңдеуімен анықталған функция:

,

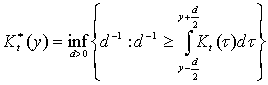мұндағы -¥<t<¥.

Теорема 2.1.1. шарты орындалсын деп ұйғарайық. Онда L операторының кеңістігінде үзіліссіз кері операторы бар.

Теорема 2.1.2. шарттары орындалсын. Онда кері операторының сандары үшін төмендегі теңсіздік орынды

мұндағы С₁ және С₂ сандары тұрақты сандар, яғни 0< С₁≤ С₂.

Негізгі нәтижені келтірмес бұрын дәлелдеуге қажетті түсініктер мен көмекші фактілерге шолу жасаймыз.

Анықтама 2.1.1. Егер үшін тізбегінің құрамында жинақты ішкі тізбек бар болса онда операторы жете үзіліссіз деп аталады.

Анықтама 2.1.2. Егер функциясы үшін шарты орындалса, онда сызықты шенелген операторы теріс емес деп аталады, және белгіленеді.

Айталық кез келген шенелген оператор болсын, онда Себебі:

Жете үзіліссіз сызықты кез келген операторы үшін операторын төмендегідей анықтаймыз: .

Анықтама 2.1.3. операторының меншікті мәндері операторының -сандары (Шмид бойынша меншікті мәндері) деп аталады.

Нөлден өзгеше -сандарының еселіктерін ескеріп кему ретімен нөмірлейміз, яғни .

Мұндағы -сандары оң және нақты сандар.

Анықтама 2.1.4. Егер компактілі операторы

шартты қанағаттандырса, онда операторы ядролы оператор деп аталады.

Айталық -банах кеңістіктері кеңістігі кеңістігіне енгізілген және жиыны кеңістігіндегі бірлік шар болсын.

Анықтама 2.1.5. жиыны кеңістігінің метрикасында мүмкін болатын өлшемі сызықты көпбейнелерінен ауытқуларының төменгі шені -дің -ге енуінің Колмогоров көлденеңдері деп аталады, яғни анықтама бойынша

мұндағы мүмкін болатын сызықты көпбейнелер жиынтығы.

мұндағы енгізу оераторы.

Тікелей анықтамадан шығатын көлденеңдердің мынандай қасиеттері бар:

1.

2.

3. мұндағы

Колмогоров көлденеңдерінің екінші анықтамасы іспеттес келесі теорема орынды болады.

Теорема. Айталық қандай да бір жете үзіліссіз оператор, онда саны жиынының -шы Колмогоров көлденеңімен сәйкес келеді, яғни .

Мұндағы бірлік шар.

Колмогоров көлденеңдерінің бұл келтірілген анықтамасы көптеген жағдайларда біріншіге қарағанда ұтымды болады.

Келесі функцияны енгізейік:

-дан үлкен көлденеңдердің саны.

Бұл функция көлденеңдерді тарату функциясы немесе санаушы функция деп аталады. -шы көлденеңдермен оларды тарату функциясының арасында мынандай байланыс бар .

Соңғы теңдік көлденеңдерді бағалау үшін олардың тарату функцияларын бағалауға болатынын білдіреді.

Теореманы дәлелдеу үшін көмекші леммалар теңсіздіктерді қарастырамыз.

Төмендегі теңдік арқылы анықталған операторды жиынында қарастырайық

мұндағы жиыны шексіз дифференциалданатын және шартын қанағаттандыратын жиын.

Лемма 2.1.1. шарты орындалсын. Онда:

а) барлық үшін төмендегі теңсіздік орынды

б) операторының үзіліссіз кері операторы бар.

Дәлелдеу. Барлық үшін төмендегі скаляр көбейтіндіні қарастырамыз:

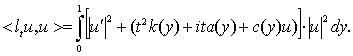
Осыдан

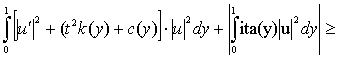
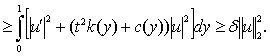
2.1.1 леммасының дәлелденді.

Лемма 2.1.2. шарты орындалсын. Онда барлық үшін төмендегі баға орынды

Дәлелдеу. Лемманы дәлелдеу үшін квадраттық форма құрып, бөліктеп интегралдау әдісін қолданамыз:

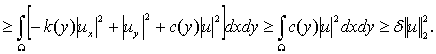
Бұл жерде, 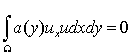екендігі ескерілді. Лемма 1.3.2 дәлелденді.

Лемма 2.1.3. шарты орындалсын. Онда барлық төмендегі баға орынды:

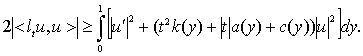
Дәлелдеу. Барлық үшін:

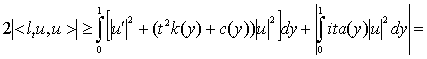
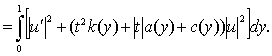
Лемма 2.1.3 дәлелденді.

Лемма 2.1.4. шарттары орындалсын. Онда кез келген үшін тұрақтысы табылып, мұндағы төмендегі теңсіздік орынды

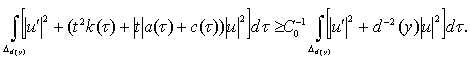
Лемма 2.1.5. шарттары орындалсын. Онда төмендегі

баға орынды

Лемма 2.1.6. шарттары орындалсын. Онда барлық үшін төмендегі баға орынды:

мұндағы С>0-тұрақты сан.

2.1.4-2.1.6 леммалары алдыңғы бөлмшедегі леммалар сияқты дәлелденеді.

Теорема 2.1.1 дәлелдеуі. Үздіксіз есептеу нәтижесінде төмендегі теңдіктің орындалатынын көреміз

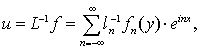
мұндағы операторы операторына кері оператор. Теорема 2.1.1 дәлелденді.

Теорема 2.1.2 дәлелдеуі. 2.1.6 лемма шартынан L операторының анықталу облысы кеңістігімен беттесетіндігі шығады.

кеңістігінің бірлік шарының Колмогоров көлденеңдері үшін келесі екі жақты баға алынады:

мұндағы - l>0 болатын -ғы бірлік шарының көлденеңдерінің саны. С- тұрақты сан.

Соңғы теңсіздіктен және қасиетінен:

(2.1.4)

аламыз.

Ары қарай, L операторына кері операторының сандары үшін теңдігін және (2.1.4) бағасын ескері төмендегі теңсіздікті

аламыз. Мұндағы С₁ және С₂ тұрақты сан, яғни 0< С₁≤ С₂. Теорема 2.2 дәлелденді.

Пайдаланылған әдебиеттер тізімі

1. Смирнов М.М. Вырождающиеся эллиптические и гиперболические уравнения. –М.: «Наука», 1966.-С.292.

2. Трибель Х. Теория интерполяции, функциональные пространства, дифференциальные операторы.-М., 1980.-С. 664.

3. Кальменов Т.Ш., Отелбаев М.О. О гладкости решений одного класса вырождающихся эллиптических уравнений //Дифф. урав. -1977. - Т.13, №7. -С. 1244-1255.

4. Келдыш М.В. О некоторых случаях вырождения уравнений эллиптического типа на границе области // ДАН СССР.- 1951. - 77, №2 -С. 181-183.

5. Олейник О.А. О гладкости решений вырождающихся эллиптических и параболических уравнений //ДАН СССР.- 1965.-vol.- 163, №3.-Р. 557-580.

6. Муратбеков М.Б. О гладкости решений одного класса неравномерно вырождающихся эллиптических уравнений // Известия АН Каз ССР. Сер.физ-мат. - 1981. - №5. - С.71-73.

7. Муратбеков М.Б. О гладкости решений одного класса неравномерно вырождающихся эллиптических уравнений высокого порядка // Корректные краевые задачи для неклассических уравнений математической физики. - Новосибирск. - 1981. - С.144-146.