Д. ф.-м. н., доц. А. В. Макаричев, А. А. Кудь, А. Б. Щукин

Московский государственный университет им. М.В. Ломоносова Харьковский национальный автомобильно-дорожный университет Национальный аэрокосмический университет «ХАИ»

УЛУЧШЕНИЕ ОЦЕНКИ А.Д. СОЛОВЬЁВА ХАРАКТЕРИСТИК НАДЁЖНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ.

В ремонтный орган (РО), представляющий собой однолинейную систему массового обслуживания, поступает пуассоновский поток с параметром требований на восстановление элементов. Требования обслуживаются в порядке поступления. Времена обслуживания требований независимы в совокупности и одинаково распределены с функцией распределения . После восстановления элемент возвращается туда, откуда он потупил. Случайный процесс обслуживания в момент времени задаётся числом элементов на обслуживании в РО. Он является регенерирующим. Моментами регенерации являются моменты перехода случайного процесса в состояние (в РО нет требований). В момент перехода этого случайного процесса из состояния в состояние наступает отказ, . Обозначим через вероятность отказа на периоде регенерации этого случайного процесса обслуживания. Пусть и .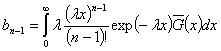

Теорема. Для всех натуральных чисел верно неравенство

.

Прежде, чем доказывать теорему докажем несколько утверждений.

Лемма 1. Пусть для чисел , , , , известно, что

для всех .

Тогда для всех справедливо неравенство

, где .

Доказательство. Из условия леммы для всех . Отсюда для всех верно , где . Пусть . Тогда из условия и последнего равенства верна цепочка соотношений

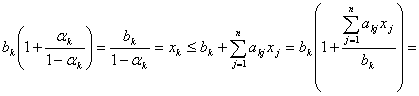
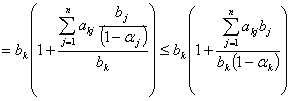
Сравнивая левую и правую части этих соотношений, мы видим, что

,

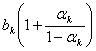
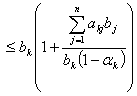и отсюда верны неравенства

.

Следовательно, для всех верно , что и требовалось доказать.

Лемма 2. Для любых неотрицательных целых чисел и

.

Доказательство. Обозначим

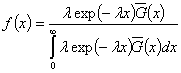и .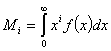

Заметим, что . Отсюда и неравенства для моментов [1]

следует цепочка соотношений

,

то есть

,

что и требовалось доказать.

Доказательство теоремы.

Обозначим условную вероятность отказа на периоде регенерации при условии, что в его начале в РО находятся ровно полных требований на восстановление элементов, (напомним, отказ наступает в случае в момент перехода системы из состояния в состояние , то есть когда неисправными окажутся элементов). В зависимости от числа отказавших элементов за время восстановления первого отказавшего элемента на периоде занятости РО по формуле полной вероятности запишем

Так же по формуле полной вероятности записываем выражение для вероятности отказа , когда вначале периода занятости в РО ровно (не менее двух) полных требований,

.

Заметим, что и , . Эти равенства и преобразование Абеля позволяют записать и оценить сверху вторые слагаемые в правых частях последних двух серий выражений соответственно в виде

(здесь по определению считаем ),

для .

Обозначим , , и по определению . Подставляя вместо вторых слагаемых в правых частях вышеозначенных выражений полученные верхние оценки для них, перенося последние слагаемые (для не менее двух) справа налево, преобразуем наши выражения для вероятностей отказов в виде равенств в неравенства для них и их разностей соответственно

для и

для .

Для этой системы неравенств в условиях леммы 1 матрица имеет вид

.

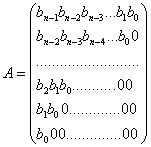Для вышеупомянутой системы неравенств используем лемму 1, взяв , . Из этой системы неравенств согласно лемме 1

, где .

Согласно лемме 2 для всех целых верно неравенство

и

.

Получив верхнюю оценку для величины , , мы тем самым оценили и вероятность отказа системы на периоде регенерации случайного процесса в модели резервирования с восстановлением

.

Следствие. Для вероятности отказа верна двусторонняя оценка

, .

Для простого дублирования, когда , эта оценка даёт точное значение для вероятности . Стоит отметить, что этим качеством не обладает полученная, вообще говоря, другим методом, похожая верхняя оценка великого нашего учителя А.Д. Соловьёва (стр. 98-100 в [2]), в которой отсутствует вычитаемая единица в скобках в знаменателе. Стоит также отметить, что при числе резервных элементов величина в скобках в знаменателе у новой оценки вдвое меньше, чем соответствующий множитель у верхней оценки этой вероятности в замечательном труде [2].

Литература

1. Гнеденко Б.В. Курс теории вероятностей. – 5-е изд. М.: Наука, 1969.

2. Вопросы математической теории надежности /Е.Ю. Барзилович, Ю.К.

Беляев, В.А. Каштанов, И.Н. Коваленко, А.Д. Соловьев, И.А. Ушаков;

Под ред. Б. В. Гнеденко.- М.: Радио и связь, 1983.- 376 с., ил.