ДЕКОМПОЗИЦИЯ
КОРРЕЛЯЦИОННОЙ ФУНКЦИИ. ПРИЛОЖЕНИЯ
Карев М.Н., Данилов А.М.
Пензенский государственный университет архитектуры и
строительства
Одной из важнейших задач повышения имитационных
характеристик тренажных и обучающих комплексов для подготовки операторов
является определение спектрального состава управляющих воздействий оператора в
процессе нормального функционирования целостной эргатической системы.
В
силу ее замкнутости через оператора практически невозможно ретроспективно определить
передаточную функцию объекта управления. Поэтому когнитивное моделирование целостной
системы производится с использованием частотных методов. Проще всего использовать
аппроксимацию корреляционной функции кусочно-линейной функцией: в виде алгебраической
суммы треугольных корреляционных функций
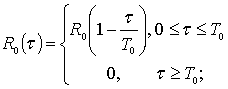
![]() .
.
Тогда
каждой типовой треугольной корреляционной функции ![]() будет соответствовать
спектральная плотность
будет соответствовать
спектральная плотность
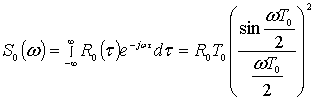 ;
; ![]() ,
, 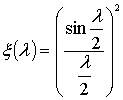 .
.
Откуда из ![]() следует
следует 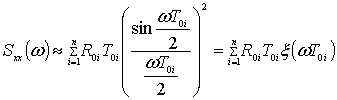 .
.
Точность
определения спектральной плотности тем
выше, чем меньше расхождение между корреляционными функциями: действительной и
результирующей аппроксимированной. При этом несоответствие в значениях функции
для малых ![]() будет преимущественно
вызывать отклонение в значениях спектральной плотности для больших
будет преимущественно
вызывать отклонение в значениях спектральной плотности для больших ![]() . При синтезе ряда тренажеров транспортных систем корреляционная
функция имела вид, приводимой на рис.1 (1- аппроксимируемая корреляционная
функция, 2 - аппроксимированная корреляционная функция;
. При синтезе ряда тренажеров транспортных систем корреляционная
функция имела вид, приводимой на рис.1 (1- аппроксимируемая корреляционная
функция, 2 - аппроксимированная корреляционная функция; ![]() - аппроксимирующие типовые треугольные корреляционные функции;
- аппроксимирующие типовые треугольные корреляционные функции;![]() ).
).
Использовался следующий приводимый ниже алгоритм
решения уравнения идентификации в частотной области. Он сводится к
последовательному выполнению процедур:
-
вычисление дискретных значений автокорреляционной функции
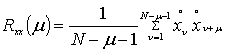 ,
,
где
интервал реализации ![]() , шаг по времени
, шаг по времени ![]() , интервал корреляции
, интервал корреляции ![]() связаны соотношениями:
связаны соотношениями:
![]() ;
; 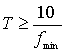 ;
; ![]() ;
;
-
построение графика ![]() ;
;
-
кусочно-линейная аппроксимация графика ![]() ;
;
-
построение графиков типовых треугольных корреляционных функций; определение ![]() и
и ![]() ;
;
-
вычисление 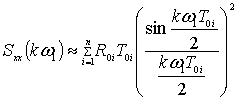 ,
, ![]() ;
;
-
вычисление дискретных значений взаимной корреляционной функции
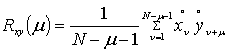 ;
;
-
вычисление ![]() ;
;
-
построение графика ![]() ;
;
-
кусочно-линейная аппроксимация графика ![]() ;
;
![]()
![]()
![]()
![]()
![]()
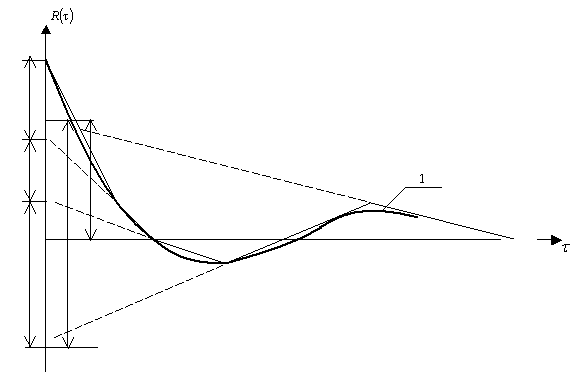

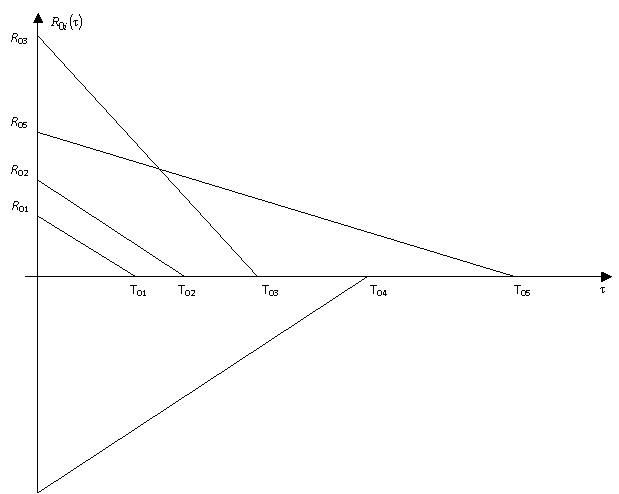

Рис.1. Пример
аппроксимации корреляционной функции типовыми треугольными корреляционными
функциями
-
построение графиков типовых треугольных корреляционных функций; определение ![]() и
и ![]() ;
;
-
вычисление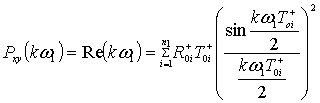 ;
;
-
вычисление ![]() ;
;
-
построение графика ![]() ;
;
-
кусочно-линейная аппроксимация графика ![]() ;
;
-
построение графиков типовых треугольных корреляционных функций; определение ![]() и
и ![]() ;
;
-
вычисление 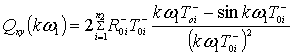 ;
;
-
вычисление вещественной частотной характеристики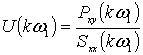 ;
;
-
вычисление мнимой частотной характеристики 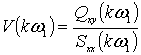 ;
;
-
вычисление амплитудной частотной характеристики
![]() ;
;
- вычисление фазовой частотной характеристики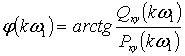 ;
;
-
аппроксимация амплитудной частотной характеристики типовыми звеньями;
-
построение фазовой характеристики.
Предложенный алгоритм использовался при
построении вибрационной карты сложной управляемой в пространстве динамической
системы и когнитивной модели управляющих воздействий оператора эргатической системы.