Технические науки/2. Механика

К.т.н. Гирнис С.Р., д.т.н. Украинец В.Н., Кошанова К.М.

Павлодарский государственный университет, Казахстан

ВЛИЯНИЕ СКОРОСТИ РАВНОМЕРНО ДВИЖУЩЕЙСЯ В ТОННЕЛЕ НАГРУЗКИ НА НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ ПОРОДНОГО МАССИВА

На основе решения задачи о действии бегущей с постоянной скоростью периодической нагрузки на толстостенную оболочку в упругом пространстве исследуется влияние скорости движения данной нагрузки на реакцию окружающего тоннель глубокого заложения породного массива.

1. Используя модельный подход, представим тоннель глубокого заложения в виде бесконечно длинной круговой цилиндрической толстостенной упругой оболочки с радиусом внешней поверхности и радиусом внутренней поверхности , расположенной в линейно-упругом, однородном и изотропном пространстве с параметрами Ламе , и плотностью . Параметры Ламе и плотность материала оболочки обозначим соответственно , ; . В дальнейшем индекс 1 относится к среде, а 2 – к оболочке. Контакт между оболочкой и окружающей её упругой средой (массивом) будем полагать либо жестким, либо скользящим при двусторонней связи в радиальном направлении.

По внутренней поверхности оболочки вдоль ее оси z с постоянной скоростью с (меньшей, чем скорости распространения волн сдвига в оболочке и окружающей ее среде) движется периодическая по z нагрузка P.

Так как рассматривается установившийся процесс, то картина деформаций стационарна по отношению к движущейся нагрузке. Поэтому удобно перейти к подвижной цилиндрической системе координат . Тогда, в случае синусоидальной с произвольной зависимостью от угловой координаты нагрузки, имеем

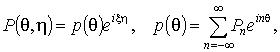
(1)

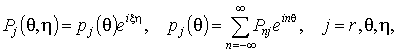
где константа x определяет период T = 2p/x действующей нагрузки, – составляющие интенсивности нагрузки .

Для описания движения упругой среды и оболочки воспользуемся динамическими уравнениями теории упругости в подвижной системе координат [1]

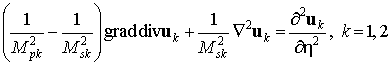, (2)

где – числа Маха; , – скорости распространения волн расширения – сжатия и сдвига в среде и оболочке, , – модули сдвига, – коэффициенты Пуассона; – векторы смещений точек пространства и оболочки, – оператор Лапласа.

Выражая вектора смещений через потенциалы Ламе [1]

, (3)

преобразуем уравнения (2) к виду

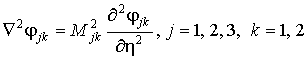. (4)

Здесь .

Используя (3), получаем выражения для компонент напряжённо-деформированного состояния (НДС) среды и оболочки

,

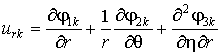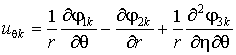, (5)

;

,,

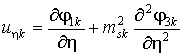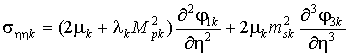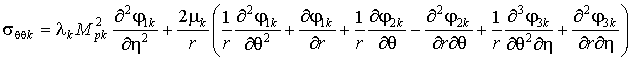
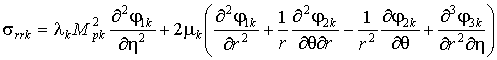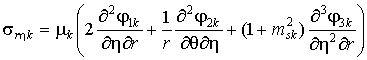, (6)

,

,

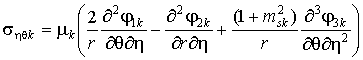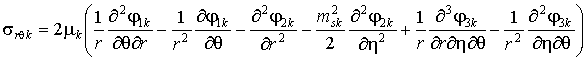где .

Таким образом, для определения компонент НДС оболочки и окружающей её упругой среды необходимо решить уравнения (4) используя следующие граничные условия:

- для скользящего контакта оболочки со средой:

при r = R₁ , , , , , ,

при r = R₂ , ; (7,а)

- для жёсткого контакта оболочки со средой:

при r = R₁ , , при r = R₂ , . (7,б)

Потенциалы j_jk также будем искать в виде

. (8)

Подставляя (8) в (4), получим

(9)

где – двумерный оператор Лапласа, .

В дозвуковом случае M_sk < 1 (m_2k = m_3k = m_sk > 0, k = 1, 2), и мы приходим к известным решениям уравнений (9):

- для массива

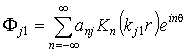, (10,а)

- для оболочки

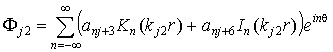, (10,б)

Здесь – функции Бесселя первого и второго рода от мнимого аргумента, , , j = 1,2,3; – неизвестные коэффициенты, подлежащие определению.

Подставляя (10,а) с учётом (8) в (5), (6), получаем формулы для вычислений компонент напряженно-деформированного состояния массива

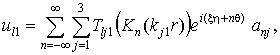
(11)

,

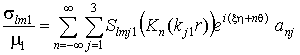где ;

,

,

,

,

, ,

,

, ,

,

,

,

,

,

;

.

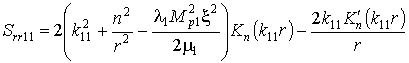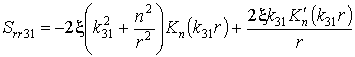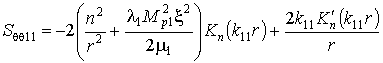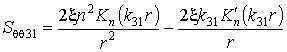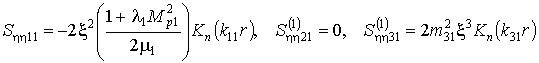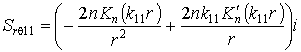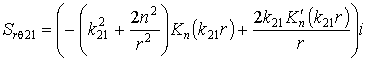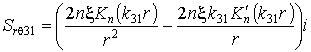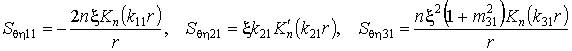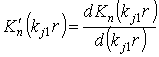Аналогично подставляя (10,б) в (1.5), (1.6), получаем формулы для вычислений НДС оболочки

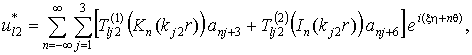
(12)

.

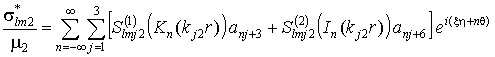Здесь ;

,

,

,

,

, ,

,

, ,

,

,

,

,

,

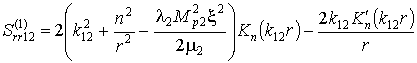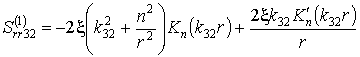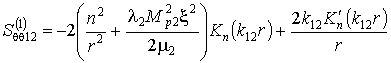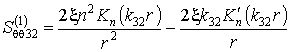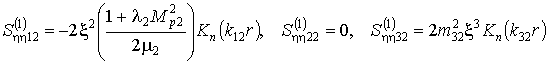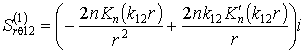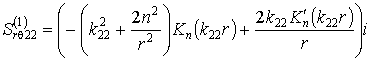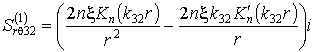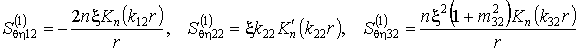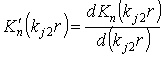; получаются из заменой на .

Для определения при фиксированном n девяти неизвестных коэффициентов , воспользуемся граничными условиями (7,а) или (7,б), с учётом (1), (11), (12). Приравнивая коэффициенты рядов при e^inq, получим бесконечную систему (n = 0, ±1, ±2,…) линейных алгебраических уравнений блочно-диагонального вида:

- при скользящем контакте

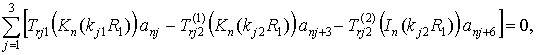
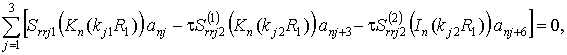
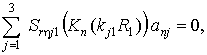
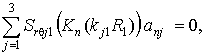(13,а)

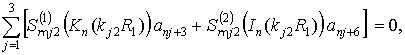
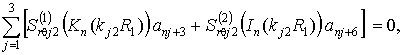
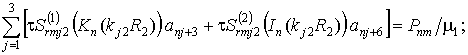
- при жёстком контакте

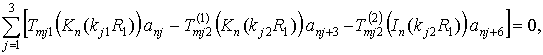
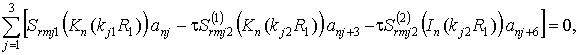(13,б)

,

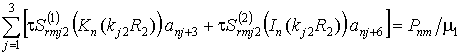где m = r, q, h, t = m₂/m₁.

Решение системы (13,а) или (13,б) находим известным методом, если соответствующий для каждого n определитель D_n(x, с) отличен от нуля.

После определения коэффициентов a_nJ (J = 1, 2,…, 9), компоненты напряжённо-деформированного состояния массива и оболочки можно вычислить по формулам (11), (12).

2. Исследуем влияние скорости движения нагрузки на напряженно-деформированное состояние массива. В качестве примера рассмотрим подкрепленный бетонной (n₂= 0,2, m₂= 1,21×10¹⁰Па, r₂ = 2,5×10³кг/м³; c_s2 = 2200,0 м/с, c_p2 = 3592,6 м/с) оболочкой с радиусами поверхностей R₁ = 1,1м, R₂ = 1м тоннель глубокого заложения в породном массиве с характеристиками: n₁= 0,25, m₁= 4,0×10⁹Па, r₁ = 2,6×10³кг/м³; c_s1 = 1240,35 м/с, c_p1 = 2148,34 м/с [2]. По внутренней поверхности оболочки с постоянной скоростью c движется осесимметричная нормальная синусоидальная (T = 2π) нагрузка с амплитудой P_A, оказывающая давление на поверхность оболочки в области начала подвижной системы координат. Контакт оболочки с массивом полагаем жестким.

В табл. 1 приведены числовые значения компонент напряженно-деформированного состояния массива в плоскости h = 0 при разных скоростях движения нагрузки. В таблице приняты следующие обозначения: u_r1^*= u_r1m₁/P_A (м), s_θθ1^* = s_θθ1/P_A, s_ηη1^* = s_ηη1/P_A.

Табл. 1 – Компоненты НДС массива в плоскости h = 0

c, м/с	ur1^*		sθθ1^*		sηη1^*
	r/R1		r/R1		r/R1
	1,0	4,0	1,0	4,0	1,0	4,0
200	0,29	0,01	0,40	0,0	-0,29	0,01
800	0,33	0,03	0,48	0,01	-0,34	0,02

Из таблицы следует, что с увеличением скорости движения нагрузки значения компонент НДС массива в окрестности подкрепленной оболочкой полости возрастают.

С удалением от границы полости эффект динамического воздействия бегущей нагрузки на массив снижается, и при r/R₁ = 4,0 становится практически мало существенным при любой из рассмотренных здесь скоростей нагрузки.

Литература

1 Ержанов Ж.С., Айталиев Ш.М., Алексеева Л.А. Динамика тоннелей и подземных трубопроводов. – Алма-Ата: Наука, 1989. – 240 с.

2 Булычев Н.С. Механика подземных сооружений в примерах и задачах. – М.: Недра, 1989. – 270 с.