д.м.н. Кокуркин Г.В., к.ф.м.н Семенов В.И., Кокуркина Р. Г.,

Денисов Ф.Т.

Чувашский государственный университет им. И.Н. Ульянова

г. Чебоксары

Сжатие сигнала

Дискретное и непрерывное вейвлет-преобразование (ВП) избыточно, так как количество вейвлет-коэффициентов превосходит число отсчетов исходного сигнала. Для того чтобы количество вейвлет-коэффициентов было равно числу отсчетов исходного сигнала, при дискретном ВП используется алгоритм субполосного кодирования (фильтрации). Данный алгоритм тесно связан с КМА. Субполосная фильтрация используется не просто для разложения и восстановления, а целью, по словам И. Добеши, является сжатие или обработка между этапами разложения и восстановления. Сжатие после субполосной фильтрации более осуществимо, чем в отсутствии фильтрации во многих приложениях. Сжатие после субполосной фильтрации производится путем отбрасывания вейвлет-коэффициентов с малым значением, без заметного искажения сигнала [1, 2, 3, 4, 5].

Таким образом, достигается уменьшение данных. Поэтому дискретное ВП широко используется для сжатия информации, так как для непрерывного ВП аналогичного алгоритма нет, для сжатия непрерывное ВП не используется.

Цель исследования: разработать алгоритм непрерывного вейвлет-преобразования для сжатия информации.

Разработанный нами алгоритм для реконструкции сигнала позволяет также применить субполосное кодирование для непрерывного ВП. Используя Sinc-вейвлет, умножая его на косинус, можно создать фильтры нижних и верхних частот. Последовательно пропуская сигнал через фильтры нижних и верхних частот и используя децимацию можно повторить алгоритм Малла для непрерывного ВП.

Рассмотрим пример сжатия сигнала, применяя быстрое непрерывное ВП, без использования децимации и интерполяции. Если исследовать вейвлет-коэффициенты или комплексно-сопряженные Фурье-коэффициенты, для разных уровней декомпозиции m, то видим, что для больших масштабных коэффициентов а вейвлет-коэффициенты почти одинаковы на всем протяжении сигнала. А Фурье-коэффициенты имеют очень мало коэффициентов с большими амплитудами.

Также энергия, приходящаяся на средние значения m для акустического сигнала, намного больше, чем на большие и малые уровни декомпозиции. Для других типов сигналов есть отличия. Сжатие информации для непрерывного ВП можно производить или в области вейвлет-коэффицентов, или в области Фурье-коэффициентов путем удаления коэффициентов с малым значением. 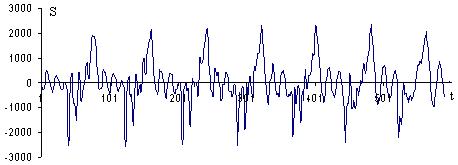Удаление коэффициентов с малым значением вейвлет-коэффициентов называется пороговой обработкой сигнала. На рис. 1 представлены графики акустического сигнала и его сжатый в 3 и в 6 раз варианты. Акустический сигнал разделен на 12 уровней декомпозиции, на рисунке представлена одна четвертая часть сигнала. Сжатие производилось в области Фурье-коэффициентов. Так как при нахождении комплексно сопряженного спектра акустического сигнала и вейвлета, спектр вейвлета на каждом уровне оставляет Фурье-коэффициенты сигнала большими в определенном частотном диапазоне, а за пределами этого диапазона с очень малыми значениями. Поэтому на каждом уровне декомпозиции достаточно оставлять коэффициенты в узком спектральном диапазоне для больших масштабных коэффициентов. Чем меньше значение масштабного коэффициента, тем шире диапазон, и центр этого диапазона смещен в сторону высоких частот.

На слух различие между исходным сигналом и его сжатым вариантом почти не заметно. Коэффициент корреляции Пирсона для сигнала, сжатого в 3 раза, равен 0,890. Для сигнала, сжатого в 6 раз, – 0,817.

а)

б)

в)

Рис. 1. Сжатие сигнала

Если мы попробуем сжать этот же сигнал, используя ПФ, результаты будут намного хуже. Уже при удалении половины Фурье-коэффициентов, восстановленный сигнал сильно исказится, потому что при ПФ теряется время появления частот в сигнале. Независимо от того, появляется ли определенная частота в сигнале вначале или в конце с определенной продолжительностью, положение и амплитуда этой гармоники будет одинаковой в Фурье-спектре. Если эта же частота появляется в начале и конце сигнала, то амплитуда этой гармоники увеличится в соответствии с суммарной продолжительностью. Иными словами, удаление какой-либо гармоники может очень сильно изменить форму сигнала. При КМА сигнал декомпозируется на несколько уровней, и появление определенной частоты какой-либо длительности проявляется на Фурье-спектре m-го уровня, на других уровнях амплитуда этой гармоники будет очень малой.

Есть много методов сжатия информации. Так же как для дискретного ВП, есть возможность сжатия сигнала с использованием вейвлет-коэффициентов. Специалисты по субполосному кодированию отдают предпочтение симметрии, так как меньшая асимметрия приводит к большей сжимаемости сигнала. Симметричные фильтры называют фильтрами с линейной фазой, т.е. они имеют линейную фазо-частотную характеристику. В отличие от дискретных вейвлетов, непрерывные вейвлеты симметричные и гладкие функции, поэтому они более пригодны для сжатия информации.

Таким образом, в отличие от дискретных вейвлетов, сжатие сигнала с использованием непрерывных вейвлетов возможно и в области комплексно сопряженного спектра, и в области вейвлет-коэффициентов, что предоставляет разработанному алгоритму реконструкции сигнала больше возможностей для выбора.

Список литературы:

1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа, М.: «Наука», 1967.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Лаборатория Базовых Знаний, 2001. 632 с.: ил.

3. Кокуркин Г.В. Вейвлет-анализ сигналов частоты сердечного сокращения / Г.В. Кокуркин, В.И. Семенов, Р. Г. Кокуркина // Materialy ҲI мezinarodni vedecko - prakticka konference «vedecky prumysl evrop-skeho kontinentu 2015» . Dil 9. Praha. – 2015.- С. 34-39.

4. Новиков Л.В. Основы вейвлет-анализа сигналов: учеб. пособие /Л.В. Новикова; ИАнП РАН. М., 1999. 152 с.: ил.

5. Секунов Н.Ю. Обработка звука на РС/ Н.Ю. Секунов. СПб.: БХВ-Петербург, 2001.1248 с.