№

Монкада Роа Милагрос дель Кармен

Магистр 1 курса, ГУАП

г. Санкт-Петербург

Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

АНАЛИЗ ЧИСЛЕННОСТИ НАСЕЛЕНИЯ ВЕНЕСУЭЛЫ И ЕГО ПРОГНОЗ ДО 2030 ГОДА

В представленной ниже статье рассмотрен вопрос анализа численности населения Венесуэлы за период с 1990 по 2017 годы. Для этого была использована функция ЛИНИЯ ТРЕНДА из MS Excel и построены пять зависимостей, на основе которых и был произведен прогноз численности Венесуэлы до 2030 года.

В таблице 1 представлен рост численности населения Венесуэлы с 1990 года по 2017 год, из которой видно, что оно имеет тенденцию постоянного роста.

Таблица 1. Население Венесуэлы, млн. чел.
№ п/п	Год	Население	№ п/п	Год	Население
1	1990	19625111	15	2004	26086018
2	1991	20097103	16	2005	26541799
3	1992	20565859	17	2006	26995172
4	1993	21031733	18	2007	27445944
5	1994	21495401	19	2008	27893688
6	1995	21957740	20	2009	28337662
7	1996	22418942	21	2010	28777176
8	1997	22878608	22	2011	29211688
9	1998	23336869	23	2012	29640935
10	1999	23794545	24	2013	30065142
11	2000	24252416	25	2014	30484936
12	2001	24710850	26	2015	30900955
13	2002	25169683	27	2016	31335113
14	2003	25628348	28	2017	31775371

Предварительный анализ показал, что между столбцами № п/п (годом) и численностью населения страны очень высокая корреляция, которая равна 0,99988581, следовательно это позволяет произвести его прогноз с большой точностью.

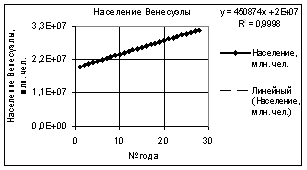
На первом рис. 1 показана зависимость численности населения Венесуэлы и порядкового номера года. Как видно из рисунка при использовании линейной зависимости получился высокий коэффициент корреляции R² = 0,9998.

Рис. 2. Население Венесуэлы

Рис. 3. Население Венесуэлы

Рис. 4. Население Венесуэлы

Рис. 5. Население Венесуэлы

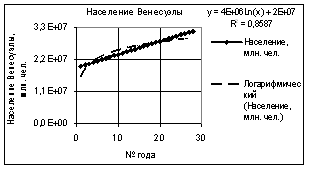
Следующий рис. 2 дает наглядное представление, что логарифмическая зависимость позволяет рассчитывать население страны менее точно, так как здесь коэффициент корреляции значительно меньше R² = 0,8587.

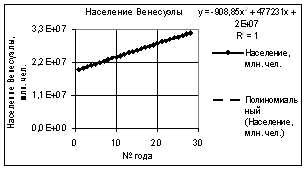
Из следующего рисунка 3 видно, что полиномиальная зависимость второго порядка, т.е. n = 2, максимально возможное значение коэффициента корреляции R² = 1.

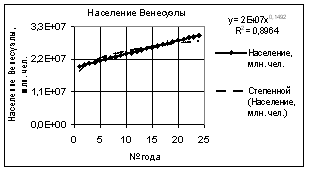
На рис. 4 показана степенная зависимость, которую также как и полученную логарифмическую не следует применять в данном примере для прогноза, так как здесь получился следующий коэффициент корреляции R² = 0,8964.

Рис. 6. Население Венесуэлы

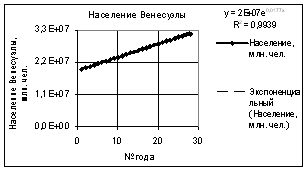
На последнем рисунке 5 показана экспоненциальная зависимость, которая также показала достаточно высокий коэффициент корреляции R² = 0,9939.

Таким образом, можно сделать вывод, что для прогноза численности населения лучше всего следует воспользоваться Линейной и Полиномиальной зависимостями.

В таблице 2 представлен прогноз численности населения Венесуэлы до 2030 года с использованием всех полученных уравнений.

Таблица 2. Прогноз численности населения Венесуэлы до 2030 года
№ п/п	Год	Линейная	Логариф.	Полин. n=2	Степен.	Экспон.
1.	2018	33075346	33469183	33075356	33053677	33415915
2.	2019	33526220	33604790	33498965	33221290	34012642
3.	2020	33977094	33735949	33920756	33384214	34620025
4.	2021	34427968	33862944	34340730	33542727	35238255
5.	2022	34878842	33986030	34758885	33697081	35867524
6.	2023	35329716	34105442	35175223	33847504	36508031
7.	2024	35780590	34221392	35589744	33994210	37159976
8.	2025	36231464	34334076	36002446	34137391	37823563
9.	2026	36682338	34443672	36413331	34277228	38499000
10.	2027	37133212	34550345	36822399	34413885	39186499
11.	2028	37584086	34654247	37229648	34547517	39886275
12.	2029	38034960	34755518	37635080	34678264	40598547
13.	2030	38485834	34854288	38038694	34806259	41323538