Секция №6. Математическая логика, алгебра и теория чисел.
Теоретико-множественная арифметика,
основанная на понятии прачисла.
Ловягин Юрий Никитич
ФГБОУ ВПО Санкт-Петербургский государственный университет,
Санкт-Петербург, Россия.
В математической логике и теории множеств имеется весьма существенный момент, связанный с обоснованием как понятия множества, так и первичных понятий логики. Автор обратил на это внимание в [1]. Там же предложен некоторый выход, основанный либо на понятии алгорифма, либо на развитии логики теории множеств, а лишь затем построение «полного» варианта математической логики и развитие на его основе теории множеств и оснований «содержательной» математики. Настоящая заметка развивает методологические идеи работы [1] путём построения натуральных чисел в рамках некоторой аксиоматики, аналогичной теории множеств Цермело – Френкеля [2]. Однако, необходимость использования некоторых «первичных» символов при описании аксиоматической системы, требует введения аналогов натуральных чисел, имеющих «наглядный вид». Это приводит к понятию прачисла, положенному в основу изложения.
1. Прачисла.
Определение 1.1. Прачисло – это объект вида:
• пустое слово («пустое место»,
слово, не содержащее ни одного символа, не занимающее место, пустой объект).
Будем обозначать всевозможные пустые объекты (слова), встречающиеся в
дальнейшем буквой 
;
• если 
есть прачисло, то
объект 
является прачислом;
• других прачисел нет.
Введём для прачисел
обозначения: 
, 
, 
, 
.
Отметим, что хотя мы обозначаем прачисла теми же символами, что и натуральные числа, разница между этими объектами существенна. Даже вводимые далее алгебраические операции и отношения равенства и порядка не превращают прачисла в «полноценные» натуральные числа.
Прачисло является
конструктивным (строимым) объектом. Поскольку прачисла строятся рекурсивно - от
простого к сложному -, для них справедлив принцип возвратной математической индукции: если из справедливости
некоторого свойства для всех прачисел строго меньших некоторого прачисла , вместе с предположением о справедливости этого свойства для
прачисла 
докзуема
справедливость его для прачисла , то свойство справедливо для всех прачисел.
Обоснование этого принципа получается из рекурсивности построения прачисел. Благодаря этому выполнение свойств прачисел можно проследить на каждом шаге его построения. И, если из того, что для предшествующих при построении прачисел следует сохранение свойства для данного числа, то свойство это переносится на один шаг. Поскольку все шаги независимы, проводить доказательство для каждого шага нет необходимости. Это и есть принцип возвратной индукции. Большинство приводимых в заметке утверждений доказывается с помощью этого принципа по некоторому параметру.
Определение 1.2. Рекурсией по строению определим равенство прачисел:
• любые два пустых объекта
равны, то есть 
;
• 
тогда и только тогда,
когда 
.
Теорема 1.1. Отношение равенства обладает свойствами:
• 
;
• если , то 
;
• если и 
, то 
для любых прачисел 
.
Определение 1.3. Сумма прачисел определяется рекурсивно:
, 
.
Определение 1.4. Будем
говорить, что прачисло меньше прачисла 
, если для некоторого прачисла 
имеет место 
. Мы пишем 
. Если и 
, то пишем 
и говорим, что
прачисло строго меньше прачисла .
Теорема 1.2. Для любых
прачисел справедливо:
• 
, 
, 
;
• если , то 
;
• если , то 
;
• если , то 
;
• если и 
, то ;
• если и 
, то 
.
2. Слова и языки.
Определение 2.1. Буквой будем называть произвольный знак. Предполагается, что имеется возможность использовать букву сколько угодно раз. Иными словами, одну и ту же букву можно воспроизводить неограниченно много раз. Воспроизведение буквы, например на бумаге, будем называть написанием. Написание буквы при наличии уже написаных называется приписыванием.
Определение 2.2. Алфавит – это список (конечный набор)
различных букв. Например, 
означает алфавит,
обозначенный буквой 
и состоящий из (трёх)
букв 
.
При задании алфавита иногда будем разделять входящие в него буквы запятыми. Отметим, что при этом предполагается, что запятая не является буквой рассматриваемого алфавита.
Наличие прачисел позволяет перечислять буквы алфавита. Имеет смысл,
таким образом, говорить о 
-буквенном алфавите. Например, 
- алфавит, состоящий
из букв 
, где - некоторое прачисло.
Определение 2.3. Слово в алфавите определяется
рекурсивно:
• пустое слово, обозначаемое
обычно - слово (объект), не
содержащее ни одной буквы;
• если 
- слово в алфавите , - буква этого
алфавита, то результат приписывания буквы к слову - объект 
является словом в
алфавите ;
• других слов в алфавите нет.
Отметим, что понятие прачисла фактически тождественно понятию слова в однобуквенном алфавите, но для общих рассмотрений его следует рассмотреть отдельно.
Определение 2.4. Равенство слов в одном и том же алфавите определяется аналогично равенству прачисел:
• любые два пустых слова
равны - 
;
• 
тогда и только тогда,
когда 
и , то есть и - одна и та же буква.
Определение 2.5. Конкатенация слов определяется рекурсивно:
, 
.
Определение 2.5. Длиной слова называется прачисло 
, определяемое рекурсивно: 
, 
.
Следующее утверждение доказывается методом возвратной математической индукции по длине слова.
Теорема 2.1. Для любых слов 
в алфавите спарведливо равенство 
.
Определение 2.6. Если имеет
место равенство 
, то говорят, что имеет место вхождение слова 
в слово . При этом класс прачисел 
называется интервалом вхождения.
Определение 2.7. Правило образования – это некоторый
процесс, согласно которому из слова в алфавите получается новое слово в
алфавите. К правилам образования отнесём приписывание
и подстановку. Приписывание
определяется как конкатенация имеющегося слова и некоторого фиксированного
слова или буквы. Подстановка это замена вхождения одного слова на другое: если 
., то 
есть результат
подстановки в слово вместо 
слова 
.
Говоря более точно, следует
определить 
как результат
следующей процедуры:
(1)
заменяем вхождение слова , которое имеет наименьшее значение левого конца интервала
вхождение – первое вхождение – на слово ;
(2) к полученному слову применяем правило (1);
(3)
если слово не имеет вхождений в
слово , то процесс останавливается и полученное слово объявляется
результатом подстановки;
(4) если процесс не останавливается, то говорим, что подстановка невозможна.
Определение 2.8. Языком называется произвольный класс слов в алфавите, который можно описать посредством правил образования. Мы рассматриваем только перечислимые языки, то есть те, слова в которых могут быть перенумерованы прачислами.
3. Язык исчисления предикатов. Алфавит языка исчисления предикатов
содержит буквы 
. На основе этих букв опишем вспомогательные языки.
Предметные переменные:
• ;
• если 
- предметная
переменная, то 
- предметная
переменная;
• других предметных переменных нет.
Обозначим 
, 
. Таким образом, предметные переменные образуют язык в двухбуквенном
алфавите 
.
Предметные константы:
• 
;
• если - предметная
константа, то - предметная константа;
• других предметных констант нет.
Обозначим 
. Таким образом, предметные константы тоже образуют язык в
двухбуквенном алфавите 
.
Говорим, что 
является предметной
переменной (константой), если 
для некоторого
прачисла 
.
Предикатные символы:
• 
;
• если - предикатный символ,
то 
- предикатный символ;
• если - предикатный символ,
то 
- предикатный символ;
• других предикатных символов
нет. Обозначим язык предикатных символов 
, определённых рекурсией
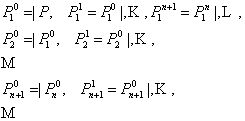
Верхний индекс является
номером предикатного символа, нижний – местностью
соответствующего символа. Мы говорим, что является предикатным
символом, если 
для некоторых прачисел
.
Функциональные символы:
• 
;
• если - функциональный символ,
то - функциональный
символ;
• если - функциональный
символ, то - функциональный
символ;
• других функциональных
символов нет. Обозначим язык функциональных символов 
, определённых рекурсией
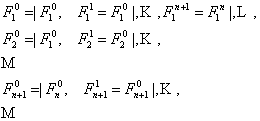
Верхний индекс является
номером предикатного символа, нижний – арностью
соответствующего символа. Мы говорим, что является
функциональным символом, если 
для некоторых прачисел
.
Определение 3.1. Термом 
называется слово,
получающееся по рекурсии согласно правилам:
• 
, где - предметная
переменная;
• 
, где 
- предметная
константа;
• 
, где 
- термы, - функциональный
символ соответствующей арности;
• других термов нет.
Определение 3.2. Атомарная формула – это слово вида 
, где - термы, 
- предикатный символ
соответствующей местности.
Определение 3.3. Формулой исчисления предикатов называется слово, построенное рекурсией согласно правилам:
• атомарная формула;
• если 
и 
- формулы исчисления
предикатов, то 
является формулой
исчисления предикатов;
• если - формула исчисления
предикатов, - предметная
переменная, то 
- формула исчисления
предикатов;
• если - формула исчисления
предикатов, то 
- формула исчисления
предикатов;
• других формул исчисления предикатов нет.
Определение 3.4. Вхождение предметной переменной в формулу исчисления предикатов будем называть собственным вхождением, если оно не является вхождением в некоторую другую предметную переменную.
В дальнейшем под вхождением предметной переменной понимается только собственное вхождение.
Определение 3.5. Вхождение
предметной переменной в формулу исчисления
предикатов называется связанным, если 
и имеет (собственное)
вхождение в . Не связанное вхождение называется свободным.
Определение 3.6. Терм называется свободным для подстановки в формулу
исчисления предикатов вместо предметной переменной
, если ни одно свободное вхождение в не является вхождением
в формулу , имеющую вид 
, где 
- предметная переменная,
имеющая вхождение в .
4. Исчисление секвенций.
Определение 4.1. Список формул – это либо пустой список,
либо объект, получающийся путём приписывания формулы исчисления предикатов к
списку формул. Списки формул будем обозначать буквами 
Определение 4.2. Секвенцией называется объект вида 
, где стрелка не является символом алфавита языка исчисления
предикатов.
Определение 4.3. Аксиомой называется секвенция вида 
.
Определение 4.4. Правилами вывода назовём фигуры вида:
• 
, 
;
• 
, 
;
• 
при условии, что как терм свободный для
подстановки в вместо , а как предметная переменная не имеет свободных вхождений ни
в одну формулу исчисления предикатов под чертой, 
при условии, что терм свободен для
подстановки в вместо .
• 
, 
;
• 
.
Определение 4.4. В правилах вывода секвенции над чертой называются посылками, под чертой – заключениями. Говорят, что заключения непосредственно следуют из посылок.
Правила вывода, как и аксиома, являются схемой, ибо в качестве списков формул (формул исчисления предикатов) могут быть написаны любые.
Определение 4.5. Выводом называется кортеж секвенций 
(для некоторого
прачисла ), в котором секвенция 
либо является
аксиомой, либо непосредственно следует из секвенций кортежа со строго меньшими
номерами. Секвенция называется выводимой,
если она является последней секвенцией некоторого вывода.
5. Теоретико-множественная арифметика.
Определение 5.1. Теорией 
называется
произвольный перечислимый класс формул исчисления предикатов, не имеющих
свободных вхождений предметных переменных.
Определение 5.2. Формула
исчисления предикатов называется выводимой из или теоремой , если для некоторого списка формул 
из класса выводима секвенция 
.
Для формулировки
теоретико-множественной арифметики нам потребуется ввести новые символы в язык
исчисления предикатов: квантор 
и логические связки 
сокращением.
Определение 5.3. Определим следующие формулы исчисления предикатов:
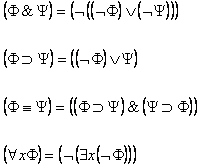
Понятия списка формул и секвенции естественным образом обобщаются и на вновь введённые формулы исчисления предикатов. При этом легко показать, что, так как каждая новая формула расшифровывается однозначно с помощью определения 5.3, понятие выводимости содержательно не меняется.
Для упрощения написания
формул мы используем приоритет связок и кванторов, позволяющий сократить
количество скобок: 
. Кванторы имеют одинаковый приоритет, совпадающий с
приоритетом отрицания. При этом «операция» более высокого приоритета
выполняется ранее. Более левая из двух одинаковых связок подряд считается более
приоритетной.
В заключении мы перечислим
список аксиом теоретико-множественной арифметики и её простейшие теоремы.
Отметим, что приводимые аксиомы отличаются от [2]. Язык теоретико-множественной
арифметики содержит два предикатных символа: равенство 
и принадлежность 
.
1. Аксиомы равенства:
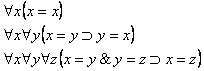
2. Аксиомы согласования с равенством:
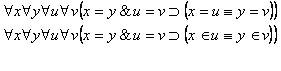
3. Аксиома
экстенсиональности: 
показывает, какие
множества считаются равными.
4. Аксиома степени: 
гарантирует
существование множества всех подмножеств. То множество, существование которого
гарантирует аксиома степени, обозначается 
. Фактически речь идёт о введении нового унарного
функционального символа в теорию.
5. Аксиома объединения: 
гарантирует
существования объединения множества , обозначаемого 
и состоящего из
элементов элементов множества .
6. Аксиома пересечения: 
гарантирует
существования пересечения множества , обозначаемого 
и состоящего из
элементов, являющихся общими элементами всех элементов множества .
7. Аксиома пары: 
утверждает
существование двухэлементного множества. По сути мы имеем дело с новым бинарным
функциональным символом, обозначаемым 
. Обозначим 
- синглетон или
одноэлементное множество.
8. Аксиома пустого множества:
утверждает, что
существует множество, не содержащее ни одного элемента. Оно обозначается 
.
Определение 5.4. Упорядоченной парой множеств и называется множество 
.
Существование упорядоченной пары следует из аксиомы пары.
9. Аксиома декартова
произведения: 
даёт существование
множества упорядоченных пар, обозначаемое 
.
Наличие приведённых аксиом позволяет доказать следующее утверждение.
Теорема 5.1. Всякое множество, существование которого гарантируется аксиомами, определено однозначно.
Наличие декартова произведения позволяет ввести естественным образом понятие функции и отношения, а также объединение и пересечение двух множеств [3]. Легко вводится и операция следования.
Определение 5.5. Обозначим
соответствующие понятия обычными знаками: 
.
Следующее определение вводит новый предикатный символ.
Определение 5.6. Множество называется подмножеством множества , если 
. Соответствующий факт обозначим 
.
Существование подмножеств
гарантируется аксиомой степени. При этом множество состоит как раз из
подмножеств множества .
Определение 5.7. Соответствием между множествами и называется
произвольное подмножество 
. Отношением
называется соответствие 
. Функцией
называется соответствие 
, для которого в теоретико-множественной арифметике доказуема
формула 
.
Определение 5.8. Определим 
. Построенные объекты назовём натуральными числами.
Определение 5.9. Сумма и произведение натуральных чисел определяется рекурсией:
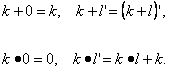
Теорема 5.2. Натуральные числа удовлетворяют аксиомам слабой арифметики [4].
Литература.
1.
Ловягин Ю. Н. О преподавании математической логики//
Некоторые актуальные проблемы современной математики и математического
образования. Герценовские чтения - 2014.
Материалы научной конференции, 14 – 18 апреля
2. Кейслер Г. Дж., Чэн Ч. Ч. Теория моделей. М.: Мир, 1977. – 614 с.
3. Ловягин Ю. Н. Элементарная математическая логика: Учебное пособие. С.-Пб: РГПУ им. А. И. Герцена, 2007 – 132 с.
4.
Ловягин Ю. Н. Арифметика А. Тарского как
методологическая основа преподавания элементарного анализа// Некоторые
актуальные проблемы современной математики и математического образования.
Герценовские чтения - 2012. Материалы
научной конференции, 16 – 21 апреля