Таттибеков К.С.
Таразский государственный педагогический
институт, Казахстан
Преобразование Дарбу для уравнения Мырзакулова - Лакшманана
Будем
исходить из уравнения Мырзакулова- Лакшманана-II (вкратце уравнения MЛ-II), которое имеет вид [1,2].
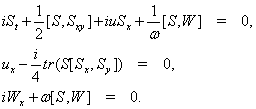(1)
Здесь 
и 
, 
- матрицы Паули, 
и 
- постоянный
параметр. Вектор 
можно
рассматривать как потенциальный вектор. Уравнение MЛ-II
интегрируемо.
Уравнение МЛ-II (1) интегрируется с
помощью МОЗР [3]. Соответствующее лаксовое представление для уравнения МЛ-II можем
написать в следующем виде
(2)
Здесь матричные операторы U и V,
соответственно, имеют формы
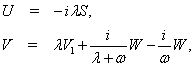(3)
Построим преобразование
Дарбу для (неизоспектральной) пары Лакса уравнения MЛ-II (1), которое позволяет строить
точные решения. Как хорошо известный метод
нахождения явных решений нелинейных уравнений в частных производных,
преобразование Дарбу первого порядка задается матрицей Дарбу 
где 
- спектральный параметр, и R и T являются
матрицами такими, что 
может быть написано в терминах решений пары Лакса [4].
Для
векторного поля рассмотрим случай 
в (1).
Преобразование Дарбу пострим следующим образом. Пусть 
будет ненулевым решением уравнения (3) при 
,
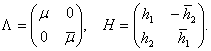(4)
Пусть
где A есть 2×2 матрица,
которая будет определен. Теперь проверим, чтобы
являлась
матрицей Дарбу для уравнения (3) при соответствущем выборе А. Для некоторого решения 
уравнения
(3), 
удовлетворяет уравнениям
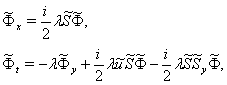(5)
для эрмитовой
матрицы 
с 
и 
и
действительной функцией 
Подставляя вместе с 
в уравнение (5),
получим 
и
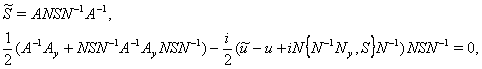(6)
где 
Для бесследной матрицы 
имеем
(7)
Заметим, что 
полученное из
уравнения (7) всегда будет вещественной и
является чисто мнимой.
Теперь a зависит только от y,
и должен
удовлетворять дополнительному уравнению
(8)
C
учетом 
, уравнение (8) эквивалентно 
Таким образом, µ должен быть решением уравнений
. (9)
Теперь решаем уравнение (9). Из второго
уравнения (9) предполагаем, что
(10)
где 
вещественные
функции. Подставляя (10) в первое уравнение (9), получим
(11)
(12)
Из уравнения (11):
(13)
где 
- произвольная
функция. Подставляя выражение для в уравнение (12) и приравнивая коэффициенты 
и 
получаем
(14)
(15)
(16)
С возможным переводом t, общее решение
уравнений (14)-(16) имеет вид
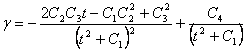(17)
или
(18)
или
(19)
Решение (18) имеет
особенность в точке t
= 0, и решение (19) делает в
уравнении (13) неопределенным за
исключением случая С1
= 0, где µ является постоянной. Пренебрегая перевод y, мы можем
установить С2
= 0.
Первое уравнение (7) подразумевает,
что a может
быть выбран как 
Предположим,
что 
является
решением уравнения (1). Пусть
где 
- вещественные
постоянные, 
Пусть 
является
решением уравнения (3) при 
Пусть
.
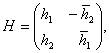
Тогда является
матрицей Дарбу для уравнения (3). Решением уравнения (1) является
который
глобально определен для всех x, y, t.
Литература
1. Myrzakulov R., Lakshmanan
M., Vijayalakshmi S., Danlybaeva A. Motion of curves and surfaces and nonlinear evolution equations in (2+1)
dimensions // Journal of Mathematical Physics. – 1998. – Vol. 39. – P. 3765-3771.
2. Myrzakulov R., Nugmanova
G., Syzdykova R. Gauge
equivalence between (2+1) - dimensional continuous Heisenberg ferromagnetic
models and nonlinear Schrödinger-type equations // Journal of Physics A: Mathematical & Theoretical. – 1998. - Vol. 31, №
47. - P. 9535-9545.
3. Захаров В.Е.,Манаков
С.В., Новиков С.В., Питаевский Л.П. –Теория солитонов: Метод обратной задачи. М.:Наука, 1980.