УДК 621.51

Д.т.н., профессор Стенин А.А.,К.т.н., доцент В.П.Пасько,

к.т.н., доцент Л.В. Сиренко

Национальный технический университет Украины «КПІ»,

Украина

ОПТИМИЗАЦИЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ МЕТОДАМИ ФУНКЦИОНАЛЬНОГО АНАЛИЗА

Аннотация: Предложен практический инструментарий методов функционального анализа для решения типовых задач оптимизации линейных динамических систем. Реализация данных методов продемонстрирована на примерах.

Ключевые слова: оптимизация, функциональный анализ, линейная динамическая система, система оптимальная по расходу топлива, система оптимальная по быстродействию

Введение

Решению задач оптимизации линейных динамических систем посвящен целый ряд фундаментальных работ [1-3], в большинстве из которых задача оптимизации решается на основе вариационного исчисления, принципа максимума и динамического программирования. Применение методов функционального анализа к решению задачи максимального быстродействия было предложено Н.Н. Красовским [4]. На основе результатов, полученных М.I. Крейном и Н.И. Ахиезером [5], он использовал для построения оптимального управления некоторые свойства функционалов в нормированных пространствах. Р.Куликовски в [6] показал, что результаты М.I. Крейна и Н.И. Ахиезера применимы при гораздо более общих предположениях относительно переменных управления. В работе [7] представлен метод динамического синтеза оптимальных законов управления как один из методов функционального анализа, в котором специально сконструированный функционал является сопровождающим для решения основной задачи обеспечения асимптотической устойчивости движения системы и заданного качества переходных процессов. Ниже предложен практический инструментарий методов функционального анализа для решения типовых задач оптимизации линейных динамических систем.

Постановка задачи

Рассмотрим задачу оптимизации управления полностью управляемой линейной динамической системы:

(1)

где – n-мерный вектор состояния системы; -мерный вектор управления; -мерный вектор наблюдения; A, B, C – матрицы коэффициентов объекта, интенсивности управления и измерителя размерности (n×n), (n×r) и (m×n).

Пусть заданы граничные условия вида:

Считаем также, то норма управления в банаховом пространстве задается в виде:

(3)

Предположим также, что вектор допустимого управления ограничен, т.е.

(4)

Из последнего условия следует, что при

(5)

Выбор нормы вектора управления в виде (3) не случаен, т.к. например, при мы имеем задачу максимального быстродействия. Действительно,

или

Кроме того, при p =2 неравенству (5) с учетом (3) отвечает ограничение на энергию управления на интервале [0,T], то есть имеем задачу оптимизации среднего значения энергии. Для p=1 это неравенство с учетом (3) означает ограниченность интеграла, взятого на промежутке времени [0,T] от суммы абсолютных значений управляющих переменных, то есть имеем задачу чистого расхода топлива.

Известно [2], что решение дифференциального уравнения вида (1) определяется следующим выражением:

(6)

где (t) – матрица перехода.

Отсюда имеем:

(7)

Необходимо найти управление, минимизирующее норму (3) и удовлетворяющее граничным условиям (2) при ограничении (4) на интервале управления [0,T].

Решение задачи

Рассмотрим вектор разности:

(8)

С учетом (7) имеем:

(9)

где матрица размерности (m×n).

Введем некоторый вспомогательный m-мерный вектор v, для которого справедливо

или (10)

Применяя неравенство Гельдера [8] с учетом соотношений (9) и (10), получим:

, (11)

где

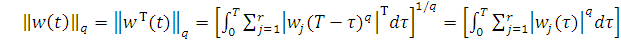(12)

или (1/p + 1/p) = 1.

Согласно неравенству (11)

(13)

Правая часть этого выражения зависит от выбора вектора v. Из равенства (8) следует, что соотношение (11) выполняется для любого вектора v. Следовательно, неравенства (11) и (13) также выполняются для любого вектора v. Отсюда следует, что

(14)

и

(15)

Исключим из рассмотрения все векторы, кроме тех, для которых Это возможно, так как не зависит от используемой формы записи (cv или v). Тогда

(16)

Обозначим через вектор, для которого норма минимальна при условии, что При этом

(17)

Тогда из соотношения (15) получим равенство:

(18)

Последнее соотношение выполняется всегда, когда неравенство

(19)

полученное из неравенства Гельдера (11), обращается в равенство. Нетрудно убедится, что неравенство Гельдера, а, следовательно, и неравенство (19) превращаются в равенства тогда и только тогда, когда выполняется условие:

(20)

для всех t

Соотношение (20) является необходимым и достаточным условием оптимальности в задачах оптимизации линейных динамических систем. На его основе нетрудно получить выражение для оптимального управления в частных случаях задач оптимизации. Например, для задачи максимального быстродействия (минимального времени перехода) в норме вектора управления (3) следует принять В этом случае норма вектора управления равна максимальному смещению M в выражении (4), что, как было показано ранее, и соответствует bang-bang-control в оптимальных по быстродействию системах [9].

Убедимся в этом следующим образом. С учетом (4) минимальное время T= T_min существует, исходя из неравенства

(21)

полученного из неравенства (19), тогда и только тогда, когда выполняется условие:

(22)

Из (22) следует, что если является непрерывной функцией T, то время T_min равно минимальному значению T, для которого

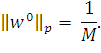
В этом случае из соотношений (20) и (23) следует, что координаты вектора оптимального управления

(24)

Наконец, учитывая то, что при , окончательно имеем:

(25)

Если неравенства (22) не выполняются ни для какого значения времени T, то для заданного ограничения M задача не имеет решения.

Как указывалось ранее, при p =1 имеем задачу чистого расхода топлива, а при p =2 – задачу оптимизации расхода энергии, для которых также нетрудно получить конечное выражения для оптимального управления.

Таким образом, решена задача минимизации времени перехода рассматриваемой линейной динамической системы при ограниченных энергетических ресурсах и при отсутствии ограничений на переменные управления.

Заключение

При достаточно общих предположениях на основе функционального анализа получены соотношения для вектора оптимального управления. Однако, для окончательного построения оптимального управления требуется решить задачу минимизации нормы (3) вектора управления, что, как правило, достаточно трудно. В отдельных случаях возможно аналитическое решение задачи оптимизации линейных динамических систем без использования численных методов и дополнительных упрощающих условий.

Литература

1. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. – М.: Наука, 1969. – 384 с.

2. Атанс М., Фалб П. Оптимальное управление. – М.: Машиностроение, 1968. – 764 с.

3. Габасов Р.А., Кириллова Ф.М. Основы динамического программирования. – Мн.: Изд-во БГУ, 1975. – 262 с.

4. Красовский Н.Н. К теории оптимального регулирования. Автоматика и управление. – 1957, т.18, № 11, СС. 960-970.

5. Крейн М.Г., Ахиезер Н.И. О некоторых вопросах теории моментов. – Харьков: ГНТИ Украины, 1938. – 256 с.

6. Куликовски Р. Оптимальные и адаптивные процессы в системах автоматического регулирования.

7. Стенин А.А., Пасько В.П., Мелкумян Е.Ю., Солдатова М.А. Анализ проблемы синтеза систем управления нелинейными динамическими объектами. Міжвідомчий науково-технічний збірник «Алаптивні системи автоматичного управління». – Київ: НТУУ «КПІ», – 2016. – Вип. 2(27), с.101– 110.

8. Соболев Л.С. Некоторые применения функционального анализа в математической физике. – М.: Наука, 1988. – 336 с.

9. Павлов А.А. Синтез релейных систем, оптимальных по быстродействию. Метод фазового пространства. Ь:, Наука. 1966. 392 с.