УДК 621.51

Д.т.н., профессор Стенин А.А.,К.т.н., доцент В.П.Пасько,

к.т.н., доцент Л.В. Сиренко

Национальный технический университет Украины «КПІ»,

Украина

РОБАСТНАЯ СТАБИЛИЗАЦИЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ C параметрической неопределенностью

Аннотация: Основная идея предложенной модальной робастной стабилизации линейных динамических систем состоит в том, что при возможных допустимых вариациях параметров объекта переходные процессы в системе стабилизации должны оставаться в пределах заданных допустимых множеств, границы которых задаются расположением корней проектируемой системы.

Ключевые слова: линейные динамические системы, робастная стабилизация, гарантированная динамика, допустимые области , модальный синтез

Введение

Одним из основных направлений повышения эффективности функционирования систем управления технологическими процессами и объектами в условиях неопределенности является синтез систем управления, которые обеспечивали бы требуемое качество функционирования. Для решения этой проблемы предложено множество подходов. Например, в [1] параметры управляющего устройства выбираются таким образом, чтобы обеспечить нечувствительность системы к произвольным неизвестным возмущениям. Некоторые способы динамической компенсации ограниченных возмущений рассмотрены в [2]. В работе [3] выделяется сигнал, несущий информацию о внешних и параметрических возмущениях системы с целью компенсации их влияния на управляемую переменную. Кроме того, актуальной задачей является выбор среди множества стабилизирующих регуляторов такого, который оптимизирует некоторый критерий, характеризующий качество управления. Наиболее распространенным ее решением является метод H_∞-оптимизации [4]. В работах [5,6] для конструирования субоптимального регулятора управляющее воздействие разложено на две составляющие: оптимальное управление, которое позволяет минимизировать заданный функционал качества, и компоненту, компенсирующую неопределенности системы управления. Целью управления является минимизация интегрального критерия качества, а компенсация неопределенностей базируется на подходе, предложенном в [2].

Данная статья является развитием указанных работ и посвящена разработке модального подхода к обеспечению робастной устойчивости линейных динамических систем в режимах стабилизации.

Постановка задачи

Пусть управляемый и наблюдаемый линейный динамический объект с неопределенностью в параметрах описывается в режимах стабилизации системой линейных дифференциальных уравнений вида:

где – n-мерный вектор состояния системы; -мерный вектор управления; A, B – матрицы коэффициентов объекта, интенсивности управления (n×n), (n× m); – неизвестная вещественная матричная функция неопределенностей размерности (n×n).

Необходимо определить оптимальное управление (t), переводящее систему (1) из заданного начального состояния (t₀) = x₀ в конечное (∞) = 0 и минимизирующее квадратичный функционал вида:

, (2)

где t₀ = 0; t_k = ∞, а Q и R – положительно определенные матрицы размерностью (n×n) и (m× m) соответственно.

В приведенной выше постановке задача стабилизации линейных динамических систем с неопределенностью в параметрах относится к линейно-квадратичным задачам оптимизации, которая сводится к решению нелинейного алгебраического уравнения Риккати для определения неизвестных коэффициентов в законе оптимального управления, представляющего собой линейную комбинацию переменных состояния искомой динамической системы. В зависимости от вида матрицы неопределенностей , существует два основных подхода к решению поставленной задачи стабилизации, связанные с решением уравнения Риккати [7].

В первом случае рассматривается система вида

(3)

где а – параметрическая неопределенность, удовлетворяющая неравенству

(4)

Тогда, согласно [7], оптимальное управление можно представить в виде:

(5)

где K – матрица коэффициентов оптимального закона стабилизации системы (1) при отсутствии матрицы неопределенностей, а k – матрица коэффициентов компенсации влияния неопределенностей на параметры системы (1), определяемая как

(6)

В формуле (6) определяется из уравнения Лурье-Риккати

(7)

Здесь где решение уравнения Риккати для системы (1) при отсутствии матрицы неопределенностей

Во втором случае считается, что матрица параметрических возмущений принадлежит некоторому множеству параметризации E при фиксированных матрицах Q и R и определяется как

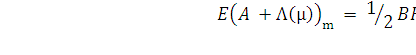(8)

где

(9)

кососимметрическая матрица, элементы которой m_i определяются по теореме Харитонова [8] о робастности линейных динамических систем. Формула (9) осуществляет канонизацию матрицы и используется в дальнейшем для определения компенсационного управления k в законе оптимальной стабилизации (5).

Обозначив канонизированную матрицу через A*, определим все множество компенсационных регуляторов k согласно работе [8] как

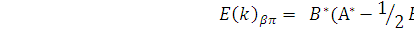(10)

где – канонизированные матрицы; – произвольная матрица подходящего размера; – кососимметрическая матрица; – правый делитель нуля максимального ранга [8]. Можно утверждать, что синтезированный таким образом регулятор (5) является робастным на множестве параметризации (8) и минимизирует функционал (2).

Рассмотренные подходы к синтезу оптимального закона стабилизации линейных динамических систем с неопределенностью в параметрах достаточно сложны в реализации и не могут обеспечить требуемые динамические показатели переходных процессов динамических систем в режимах стабилизации. Этих недостатков лишена предлагаемая модальная робастная стабилизация.

Модальная робастная стабилизация

С учетом (1) и (5) запишем уравнение замкнутой оптимальной системы в виде:

(11)

Пусть заданы ограничения на элементы матрицы параметрической неопределенности связанные с погрешностью идентификации, т.е.

(12)

а также показатели качества на переходные процессы для переменных состояния в виде:

(13)

Требуется синтезировать закон управления (5) при условиях (12) и обеспечить заданные показатели качества переходных процессов (13) в системе стабилизации линейных динамических систем с параметрической неопределенностью.

Предлагаемая ниже модальная робастная стабилизация базируется на принципе гарантированной динамики [9]. В основу этого принципа положена концепция допустимости, использующая в качестве оценки первичные показатели качества переходных процессов.

Запишем уравнение (11) в координатной форме

(14)

В соответствии с работой [9] условия (13) выполняются, если

(15)

Подставляя выражение (14) в (15) получим

(16)

где

Зададим в виде

. (17)

где выбираются как оценки максимально возможных отклонений начальный момент времени, а определяется из условия заданной степени затухания переходного процесса (рис.1) и одинаково для всех переменных состояния,т.е.

(18)

где

Указанные динамические показатели переходных процессов обеспечиваются выбором спектра корней замкнутой оптимальной системы [10].

С учетом (13), (17) и (18) уравнение (16) примет вид:

(19)

где

Рис.1.Границы допустимой области изменения i-го параметра

Интегрируя неравенство (19) на интервале получим систему линейных алгебраических неравенств

(20)

Отсюда следует, что множество значений , удовлетворяющее (20), обеспечивает робастность системы (1) к параметрическим возмущениям (12) на основе закона управления (5), полученного приведенной выше процедурой модального синтеза. Одним из вариантов практического определения значений компенсационных регуляторов является решение системы равенств (20) на границах допустимых областей и с помощью известных численных методов.

Заключение

Предложен подход к синтезу робастных систем управления в условиях параметрической неопределенности линейной стационарной модели объекта управления. Процедура модального синтеза базируется на принципе гарантируемой динамики, что позволяет решить проблему не только устойчивости, но и требуемого качества управления, и состоит в том, что при возможных допустимых вариациях параметров объекта, переходные процессы в системе стабилизации должны оставаться в пределах заданных допустимых областей (множеств) гарантированным образом. Границы этих множеств задаются соответствующим расположением корней проектируемой системы и заданной допустимой погрешностью идентификации параметров.

Литература

1. Поляк Б. Т., Щербаков П. С. Робастная устойчивость и управление. – М.: Наука, 2002. – 303 с.

2. Цыкунов А. М. Алгоритмы робастного управления с компенсацией ограниченных возмущений // Автоматика и телемеханика. – 2007. – № 7. – с. 103–115.

3. Бобцов А. А., Пыркин А. А. Компенсация гармонического возмущения в условиях запаздывания по управлению // Изв. РАН. Теория и системы управления. – 2008. – № 4. – с. 19–23.

4. Методы классической и современной теории автоматического управления. Теория оптимизации автоматического управления / под ред. К. А. Пупкова и Н. Д. Егупова. – М.: Изд-во МГТУ им. Н. Э. Баумана. – 2004. – Т. 4. – 744 с.

5. Atassi A. N., Khalil H. K. Separation principle for the stabilization of class of nonlinear systems // IEEE Trans. Automat. Control. – 1999. – Vol. 44, N 9. – P. 1672–1687.

6. Галяув Е. Р., Фуртат И. Б. Робастное субоптимальное управление линейными объектами по выходу // Информационно-измерительные и управляющие системы. – 2010. – № 8. – с. 24–31.

7. Буков В.Н. Аналитический синтез робастных регуляторов на основе параметризации уравнения Лурье-Риккати / В.Н. Буков, Н.И. Сельвесюк // Автоматика и телемеханика. – 2007. – №2. – с. 6-16.

8. Буков В.Н. Решение матричных уравнений методом канонизации / В.Н. Буков, В.Н. Рябченко, В.В. Косъянчук, Е.Ю. Зыбин // Вестник Киевского ун-та : Сер. Физ.-мат. науки.– К.: Изд-во Киевского нац. ун-та, 2002. – Вып. 1. – с. 19-28.

9. Оморов Т.Т. Принцип гарантированной динамики в теории систем управления. Кн.1.Бишкек.-Илим.2001.-150с.

10. А.А.Стенин, О.И.Лисовиченко, М.М.Ткач, В.П.Паськo. Модальный синтез оптимальных законов стабилизации линейных стационарных систем Bulgarian Journal for Engineering Design, issue. Mechanical Engineering Faculty, Technical University-Sofia.№ 30, 2016.pp.11-16.