моделирование биотехнологического процесса анаэробного сбраживания с применением кинетических уровнении

Таразский Государственный Университет им. М.Х.Дулати, г.Тараз

Доумчариева Ж.Е., Момбаев К.Ж.

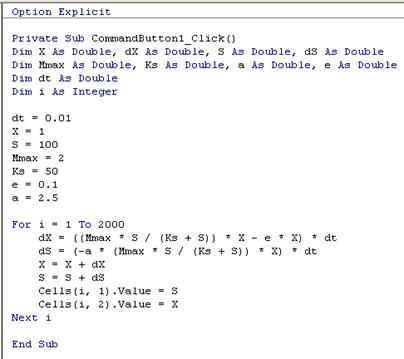
Программируем модель

µ_max будем обозначать латинскими буквами Mmax, ε будем обозначать латинской буквой e. В таком случае система уравнений будет выглядеть так:

dX/dt = (Mmax*S/(Ks + S))*X – e*X

dS/dt = – a*(Mmax*S/(Ks + S))*X

Для дальнейшего программирования перенесём dt в правую часть уравнения.

dX = ((Mmax*S/(Ks + S))*X – e*X)*dt

dS = (– a*(Mmax*S/(Ks + S))*X)*dt

Теперь программа умеет считать изменения численности (биомассы) микроорганизмов и концентрации субстрата (соответственно dX и dS) за время dt.

Но нас интересует не изменение биомассы и субстрата, а их реальные значения. Следовательно, изменения надо прибавить у текущим значениям X и S. Вот так:

X=X+dX

S=S+dS

Скорость выхода метана зависит от концентрации органического вещества S в исходном субстрате. Концентрация органического (сухого беззольного) вещества в осадке, кг/м³, зависит от влажности W, зольности на сухую массу А и объемной плотности осадка :

.

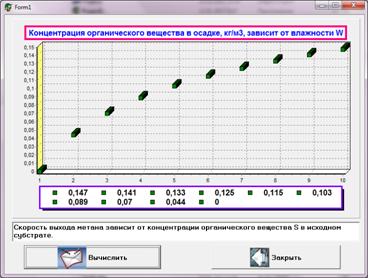
Рисунок 1. Концентрация органического вещества в загружаемом осадке

Максимальная удельная скорость роста биомассы зависит от температуры сбраживания и рассчитывается по формуле:

где t - температура сбраживания, °С.

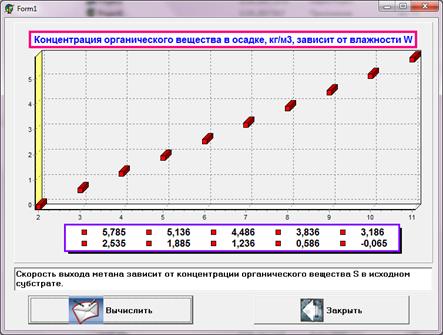
Рисунок 2. Максимальная удельная скорость роста биомассы зависит от температуры

скорость выхода метана, м³СН₄/(м³∙сут)

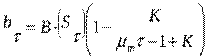
Рисунок 3. Скорость выхода метана, м³СН₄/(м³∙сут) предельный выход метана на единицу массы загруженного в метантенк органического вещества при бесконечно большой продолжительности процесса

Литература

1. Пайтген Х.О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М., Мир, 1993, 176 с.

2. Ризниченко Г.Ю., Рубин А.Б. Математические модели биологических продукционных процессов. М., Изд. МГУ, 1993, 301 с.