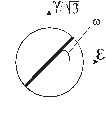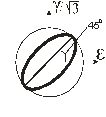К.т.н. Гладський М.М., к.т.н. Фролов В.К., Артюшенко В.В., Трибрат К.О.

Національний технічний університет України
«Київський політехнічний інститут імені Ігоря Сікорського»

Малоциклова втома металевих сплавів при непропорційному навантаженні

Ключові слова: малоциклова втома, непропорційне навантаження.

Abstract. Дана стаття присвячена розробці методу оцінювання малоциклової втоми металевих сплавів різного типу (з різною структурою) за умов непропорційного малоциклового навантажування. Наведено результати експериментальних досліджень з малоциклової втоми технічно чистого титана ВТ1-0 під час пропорційного і непропорційного двовісного навантажування. Запропоновано метод оцінювання малоциклової міцності, який дозволяє в умовах пропорційного і непропорційного малоциклового навантажування оцінити довговічність металевих сплавів з різними рівнями чутливості до непропорційності навантажування.

Вступ. Багато відповідальних елементів конструкцій у машинобудівній, аерокосмічній, транспортній, нафтогазовій, енергетичній та інших галузях промисловості працюють в умовах багатовісного малоциклового навантажування.

Результати експериментальних досліджень металевих сплавів на малоциклову втому свідчать про те, що такі фактори, як вид напруженого стану і форма траєкторії навантажування суттєво впливають на процеси їх деформування та руйнування. При цьому виявлено суттєві розбіжності в поведінці матеріалів під час навантажування за непропорційними та пропорційними траєкторіями.

Крім того, ефекти, які супроводжують непропорційне навантажування, проявляються з різною інтенсивністю у матеріалах з різною структурою, тобто є матеріали більше і менше чутливі до непропорційності навантажування.

В роботі проводиться оцінювання граничного стану металевих сплавів та елементів конструкцій, що працюють в умовах складного малоциклового навантажування.

Експериментальні результати. З метою моделювання однорідного напруженого стану всі дослідження проводились на тонкостінних циліндричних трубчастих зразках (рис. 1).

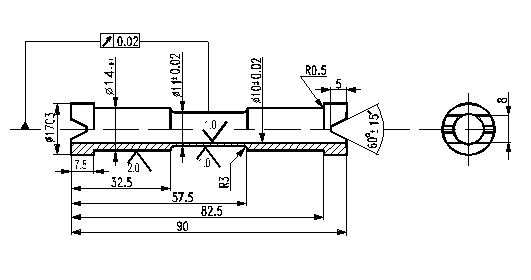
Рис. 1. Креслення зразка

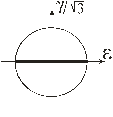
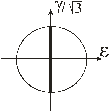
Загальна програма експериментальних досліджень складалася з таких випробувань при одновісному і неодновісному навантаженні. Типи траєкторій зображено на рис. 2.

1	2	3	4	5
Рис. 2. Типи траєкторій деформування

У просторі повних деформацій складові осьової деформації і деформації зсуву визначалися так:

, ,

де , – амплітуда осьової деформації та деформації зсуву відповідно, – колова частота, – кут зсуву фаз. Випробування за пропорційними та непропорційними траєкторіями деформування (3, 4, 5) виконувалися відповідно до плану повного двофакторного експерименту. За функцію відгуку було взято десятинний логарифм довговічності .

Випробування здійснювали на трьох рівнях еквівалентної деформації типу Мізеса: 0,7 %; 0,9 %; 1,1 % та на трьох рівнях параметру непропорційності: 0; 0,5; 1.

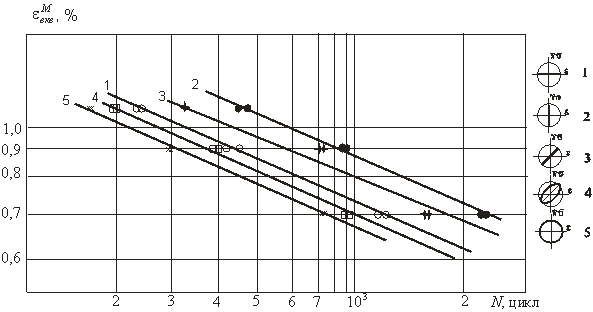
Криві довговічності титанового сплаву ВТ1-0 під час пропорційного та непропорційного навантажувань зображено на рис. 3. Результати випробувань трубчастих зразків за пропорційними траєкторіями продемонстрували, що довговічність сплаву ВТ1-0 суттєво залежить від кута орієнтації траєкторії деформування , який характеризує вид напруженого стану (у випадку розтягання-стискання дорівнює 0, а у випадку знакозмінного кручення 1). За однакових значень еквівалентної амплітуди деформації типу Мізеса найбільше число циклів до руйнування було зафіксовано для кручення, а найменше – для одновісного розтягання-стискання.

Рис. 3. Криві малоциклової втоми сплаву ВТ1-0 під час пропорційного та непропорційного навантажувань

Методика оцінювання довговічності. За базову критеріальну модель оцінювання граничного стану в умовах багатовісного малоциклового навантажування було обрано деформаційну модель, розроблену групою японських авторів Іто–Сакане–Онамі–Сосі [1]. За цією моделлю розмах еквівалентної деформації під час непропорційного навантажування визначається за формулою

, (1)

де – характеристика матеріалу, яка залежить від величини додаткового зміцнення; – параметр непропорційності, що відображає складність траєкторії деформування; – максимальний розмах головної деформації.

При розробці методу оцінювання малоциклової міцності матеріалів з різною чутливістю до непропорційності навантажування було запропоновано шукати розмах еквівалентної деформації , у вигляді аналогічному рівнянню (1), але з іншими складовими:

, (2)

де – параметр, який є мірою чутливості матеріалу до непропорційності навантажування і враховує не тільки ефект додаткового зміцнення, а й зниження довговічності; – параметр, який є мірою непропорційності траєкторії деформування; – еквівалентна деформація, знайдена за тим критерієм граничного стану, який дає найкращі результати при пропорційному навантажуванні.

У роботі використано ідею М. В. Бородія [3]щодо визначення коефіцієнта чутливості через зниження довговічності. Пропонується наступна формула для його розрахунку

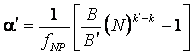, (3)

де значення і знаходяться як точки перетину кривих втоми з віссю ординат; – тангенс кута нахилу кривої довговічності для непропорційного навантажування; – тангенс кута нахилу кривої довговічності «розтягання-стискання».

У результаті проведених досліджень запропоновано еквівалентну деформацію під час непропорційного малоциклового навантажування визначити таким чином

, (4)

де – коефіцієнт чутливості матеріалу до непропорційності навантажування, розрахований за формулою (3) і для визначення якого треба мати криву малоциклової втоми розтягування-стискання та криву малоциклової втоми непропорційного навантажування, а у разі відсутності необхідних експериментальних даних з малоциклової втоми при непропорційному навантажуванні для матеріалу, що досліджується, пропонується визначати цей коефіцієнт за допомогою підходу Ліу-Махадевана [2]:

, ;

; (5)

– параметр непропорційності циклу деформування (за Іто–Сакане–Онамі–Сосі), який залежить тільки від геометрії траєкторії деформування і що визначається з наступної залежності:

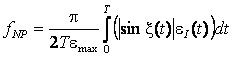; (6)

де , ,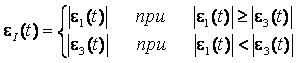

Т – тривалість циклу; x(t) – кут між напрямами e_Іmax та e_І(t); e₁(t), e₃(t) – значення максимальної та мінімальної головних деформацій у момент часу t;

– еквівалентна деформація типу Писаренка–Лебедєва [4] в деформаційному трактуванні:

,

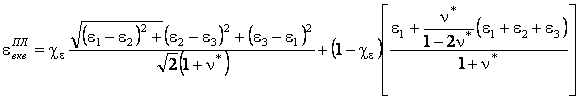де 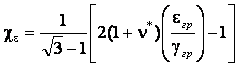; , , – величини головних деформацій; – гранична амплітуда деформації зсуву в умовах чистого кручення для заданої бази випробувань; – гранична амплітуда повздовжньої деформації в умовах розтягання-стискання для цієї ж довговічності.

Коефіцієнт поперечної деформації розраховується за формулою

.

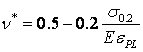Критеріальне рівняння (3) у разі пропорційного навантажування вироджується у відоме рівняння Писаренка–Лебедєва, яке записується через деформації.

На рис. 4, 5 наведено розраховані криві малоциклової втоми. Результати розрахунків свідчать про достатню погодженість методу з експериментом і надійність одержаних рівнянь для металевих сплавів з різною чутливістю до непропорційності навантажування.

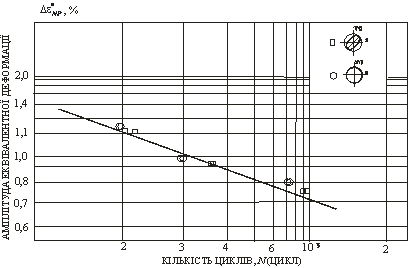
Рис. 4. Теоретична крива малоциклової втоми сплаву ВТ1-0, розрахована за рівнянням (7) з використанням виразу (3) для визначення

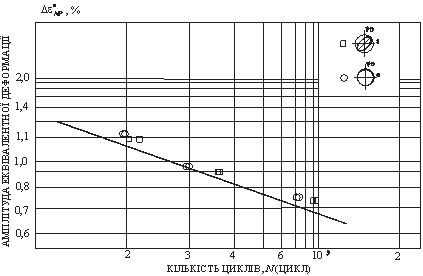
Рис. 5. Теоретична крива малоциклової втоми сплаву ВТ1-0, розрахована з використанням рівнянь (7) та (5)

Список використаної літератури

[1] Itoh T., Sakane M., Ohnami M., Kida S., Sosie D. F. Dislocation Structure and Non-Proportional Hardening of Type 304 Stainless Steel. // In: Proceeding of the 5th International Conference Biaxial-Multiaxial Fatigue and Fracture, Cracow. - 1997. - vol. 1. - pp. 189 – 206.

[2] Liu Y., Mahadevan S. Strain-based multiaxial fatigue damage mogelling // Fatigue Fracture Engn Mater Struct, 2005, – Vol. 28. – pp. 1177-1189.

[3] Borodii M.V. Stizhalo V.A. Analysis of the experimental data on a low cycle fatigue under nonproportional straining // Int. J. Fatigue. – vol. 22 – 2000 – pp. 275–282.

[4] Писаренко Г.С., Лебедев А.А. Деформирование и прочность материалов при сложном напряженном состоянии. – К. Наукова думка, 1976. – 416 с.