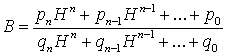К.т.н. Бесараб О.Б.

Національний технічний університет України

Київський політехнічний інститут імені Ігоря Сікорського

Вибір функції апроксимації основної кривої намагнічування вимірювального електромагнітного трансформатора напруги для дослідження ферорезонансних процесів

Для моделювання нелінійних індуктивних елементів найбільш часто застосовують основну криву намагнічування, що представляє собою геометричне місце точок вершин гістерезисних кривих, які отримують при циклічному перемагнічуванні осердя. Вона може бути представлена у вигляді залежностей потокозчеплення від струму намагнічування обмотки або магнітної індукції від напруженості магнітного поля.

У роботі [2] автором пропонується до використання низка способів апроксимації кривих намагнічування. Розглянемо їх детальніше.

Кусочно-лінійна апроксимація

Даний спосіб апроксимації передбачає заміну реальної кривої ламаною з кількома точками злому. Кількість лінійних ділянок залежить від необхідної точності відображення кривої намагнічування та діапазону її зміни.

Основною перевагою використання кусочно-лінійної апроксимації є можливість переходу до розв’язку лінійної задачі. А основним недоліком даного наближення є стрибкоподібна зміна похідної при переході від однієї ділянки до іншої, що може призвести до недопустимого значення похибки під час використання числових методів. Тому при дослідженні ферорезонансних схем використання даної функції апроксимації є обмеженим.

Гіперболічна апроксимація

Для апроксимації основної кривої намагнічування в області наближеній до насичення може використовуватися гіперболічна функція

де , – коефіцієнти апроксимації.

Застосування даної функції обмежено апроксимацією лише областей сильних полів, тому при дослідженні ферорезонансних схем використання даної функції апроксимації є нераціональним.

Логарифмічна та експоненціальна апроксимації

Використання даних функцій апроксимації обмежене задачами розрахунку магнітних кіл із постійними полями, тому при дослідженні ферорезонансних схем використання даної функції апроксимації є недопустимим.

Апроксимація степеневими поліномами, гіперболічними синусом і тангенсом

Широке застосування при апроксимації кривої намагнічування мають степеневі функції, так як вони дозволяють виконувати розрахунки магнітних кіл зі змінними магнітними полями. В загальному випадку степеневі поліноми для моделювання кривих намагнічування мають вигляд:

де , , … – коефіцієнти апроксимації.

Точність апроксимації реальної кривої степеневим поліномом пропорційна кількості членів поліному. Однак збільшення кількості членів поліному призводить до ускладнення визначення коефіцієнтів поліному.

Функції гіперболічних синуса та тангенса при розкладанні в ряд перетворюються у степеневі поліноми. Апроксимація гіперболічними синусом та тангенсом за властивостями та точністю близькі до апроксимації степеневим поліномом.

Апроксимація методом сплайнів

Метод сплайнів є доволі ефективним за умови пред’явлення жорстких вимог до точності апроксимації кривої намагнічування. За рахунок застосування різних апроксимуючих функцій, на окремих ділянках кривої намагнічування, досягається неперервність не тільки самої сплайн-функції, але і її похідної. Обмеженням використання методу сплайнів є громіздкість розрахунків.

Апроксимація раціональними функціями

Високої точності апроксимації кривої намагнічування вдається досягнути використанням раціональних функцій наступного вигляду

де , ( при ) – коефіцієнти апроксимації.

Апроксимація арктангенсними функціями

Найбільш поширеною, серед акрктангенсних функції, для апроксимації кривої намагнічування є функція арктангенса з трьома коефіцієнтами та лінійним членом:

де – коефіцієнти апроксимації.

До функції, яка апроксимує характеристику намагнічування, пред’являється низка вимог, які детально розглянуті у роботі [1]. Серед усіх розглянутих функцій задовольняють вимогам наступні: арктангенса з трьома коефіцієнтами та лінійним членом, степеневий поліном та раціональна функція. Для моделювання реальних процесів слід використовувати одну із цих 3 функцій, а саме ту, яка найбільш точно відтворює реальну криву намагнічування.

Література:

1. Бесараб О.Б. Моделювання ферорезонансного процесу в трансформаторі напруги прямим методом / О.Б. Бесараб, Ю.І. Тугай // Праці ІЕД НАНУ. – 2011. – Вип. 30. – С. 87–90.

2. Матюк В.Ф. Математические модели кривой намагничивания и петель магнитного гистерезиса. Часть I. Анализ моделей / В.Ф. Матюк, А.А. Осипов // Неразрушающий контроль и диагностика. – 2011. – № 2. – С. 3–35.