К.т.н. Земцова О.Г.

Пензенский государственный университет архитектуры и строительства, Россия

Методика учета образования трещин при расчете железобетонной балки на изгиб

При расчетах железобетонных элементов необходимо использовать методику, позволяющую учитывать появление и развитие трещин в слое бетона в элементах конструкций в зависимости от уровня нагружения и других условий. Рассмотрим методику учета образования трещин при расчете на примере изгибаемой железобетонной балки. Напряжения в бетоне и арматуре описываются зависимостями

(1)

Коэффициенты и определяются по формулам:

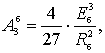
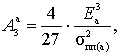(2)

где Е_а– модуль упругости стали; Е_б – начальный модуль упругости бетона; σ_пп(а) – предел временного сопротивления стали; R_б – расчетная прочность бетона.

Деформация ε определяется с использованием гипотезы плоских сечений

(3)

где y – геометрическая координата; v – вертикальное перемещение (прогиб).

Дифференциальное уравнение равновесия балки получим в результате ряда преобразований:

(4)

Учет внутренних усилий в бетоне

(5)

Полагая, что дробление сжатой зоны при продольном изгибе не наступит, для быстроты вычисления момент в бетоне от изгиба можно вычислить при помощи интеграла:

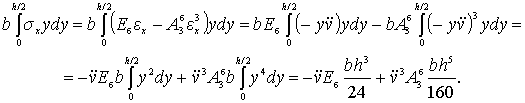(6)

Обозначим

(7)

Тогда первое слагаемое в формуле (5) примет вид:

(8)

Для определения момента в бетоне растянутой зоны численное интегрирование заменяем суммированием. Для этого делим площадь сечения балки в случае плоского изгиба на β участков-полос шириной d.

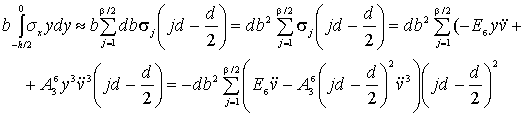(9)

Формула (5) приобретает вид:

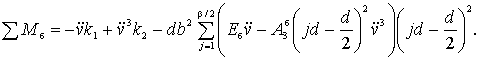(10)

Учет внутренних усилий в арматуре

(11)

Дифференциальное уравнение равновесия балки имеет вид:

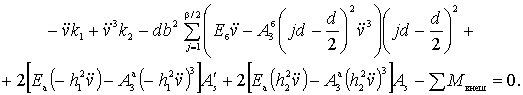(12)

Для решения дифференциального уравнения используем конечно-разностную аппроксимацию производных; для этого делим балку на n участков длиной Δ. Дифференциальное уравнение (12) заменяем системой нелинейных уравнений:

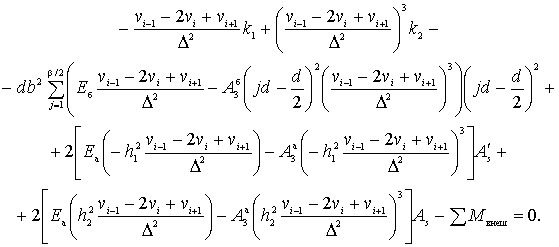(13)

Для учета трещинообразования используется соотношение

(14)

где – нормативное значение деформации при растяжении. При невыполнении условия (14) участок-полоса (или участки) исключается из расчетной части бетонного сечения

Полученная система нелинейных уравнений (13) и система ограничений (14)-(15) используется для определения напряженно-деформированного состояния изгибаемой железобетонной балки с учетом трещинообразования.

Литература:

1. Шеин А.И., Земцова О.Г. Моделирование и исследование динамики железобетонных балок в условиях трещинообразования: моногр. Пенза: ПГУАС, 2014. 123 с.

2. Земцова О.Г., Володин В.А. Комплексы программ, применяемые для моделирования и расчета конструкций зданий и сооружений [Электронный ресурс] // Моделирование и механика конструкций. 2015. №1.