Беляева А.Ю.
Национальный технический
университет Украины
«Киевский политехнический
институт»
Разработка модели
динамической системы шарикового подшипника
Подшипник есть сборочный узел, как известно. Он является
частью опоры или упора. Он поддерживает вал, ось или иную подвижную конструкцию
с заданной жёсткостью. Ни один вращающийся вал не обходится без подшипника, так
как подшипник – это тот необходимый узел, который позволяет вращаться валу, оси
или иной конструкции.
Так же
известно, что достоинствами подшипников качения являются: малые моменты трения при
обычных скоростях; малые пусковые моменты трения’ простота ухода и малый расход
смазочных материалов; высокая степень стандартизации; взаимозаменяемость и
невысокая стоимость при массовом автоматизированном производстве; малые
габариты по длине вала.
К недостаткам относятся: снижение
долговечности при высоких скоростях; значительные габариты по диаметру;
недостаточная точность направления. ограниченная
возможность применения при очень больших нагрузках и высоких скоростях;
непригодность для работы при значительных ударных и вибрационных нагрузках
из-за высоких контактных напряжений и плохой способности демпфировать
колебания; значительные габаритные размеры в радиальном направлении и масса;
шум во время работы, обусловленный погрешностями форм; сложность установки и
монтажа подшипниковых узлов; повышенная чувствительность к неточности
установки; высокая стоимость при мелкосерийном производстве уникальных по
размерам подшипников [1].
В начале рассмотрим
динамическую модель шарикового подшипника, а далее составить дифференциальные
уравнения и связать их тепловыми процессами. Следующим шагом будет
использование программы симулинк при помощи которой будут построены графики, возможность
посмотреть изменение тепловых величин в шариках и кольцах при изменении скорости
вращения вала, так как это, наверное,
самые важные элементы в подшипнике.
Динамическую модель
предлагаю следующего вида:
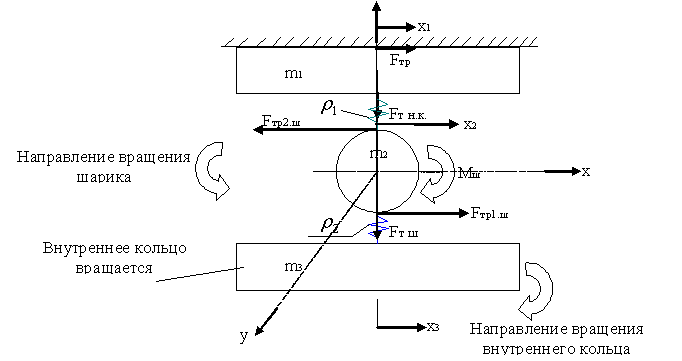
Рис. 1. Динамическая модель
шарикового подшипника
Здесь 
, - масса внешнего
кольца, 
- масса шарика 
- масса внутреннего
кольца. 
- плотность смазки
между шариком и внутренним кольцом; 
- плотность смазки
между шариком внешним кольцом, 
- сила трения шарика
с внешним кольцом; 
- сила трения шарика
с внутренним кольцом, 
- сила трения между внешним кольцом и корпусом, 
- крутящий момент шарика, 
- сила тяжести шарика;
- сила тяжести наружного
кольца. Так же будет учитываться приведенный
момент инерции ротора двигателя привода подач 
с крутильным моментом
и углом поворота ротора 
.
Далее необходимо составить дифференциальные уравнения и связать их с
тепловыми процессами. Следующим шагом будет использование программы симулинк.
При помощи данной программы будут построены графики. А также будет возможность
посмотреть изменение тепловых величин в шариках и кольцах при изменении
скорости вращения вала, так как это,
наверное, самые важные элементы в подшипнике.
Литература
http://snr.com.ru/e/about_bearings/about_bearing.htm
A.Y. Bieliaieva
National Technical University of Ukraine
"Kiev
Polytechnic Institute"
Development of a model of dynamic system of a ball bearing
The bearing
is subassembly, as is generally known. It is part of support. It supports a
shaft, axis or another movable construction with the given the rigidity. Not a
single torsion shaft does without bearing, because bearing is that necessary
knot, that allows to torsion shaft, axis or another construction.
It is also
known that the advantages of rolling bearings are small moments of friction at
normal speed; small starting torque friction 'easy care and low consumption of
lubricants; high degree of standardization; interchange ability and low cost in
mass automated production; small dimensions along the length of the shaft.
The disadvantages include: reduced durability at high
speeds; significant size in diameter; lack of direction accuracy; limited the
possibility of applying for very high loads and high speeds; unfitness for work
under considerable shock and vibration loads due to high contact stress and
poor ability to dampen vibrations; significant dimensions in the radial
direction and weight; noise during operation due to errors in the forms; the
complexity of the setup and installation of bearing units; Hypersensitivity to
installation errors; the high cost of small-scale production with unique size
bearings [1].
In the beginning we consider a model of dynamic system
of a ball bearing, and then make the dynamic equations and link them by thermal
processes. The next step is to use simulink program by means of which will be
built graphics, the ability to see the change in heat value in the balls and
rings when changing the shaft speed, since it is probably the most important
elements in the bearing.
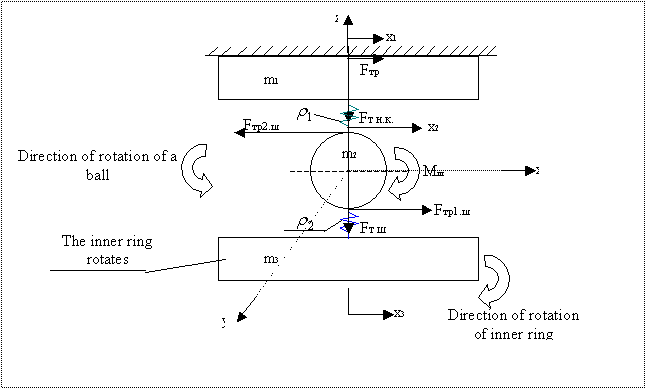
Fig. 1. Scheme of a model of dynamic system of a ball bearing
Here:
, - the mass of the outer ring,
- the mass of the ball;
- the mass of the inner ring;
- lubrication density between
the ball and the inner ring;
- lubrication density between
the ball and outer ring,
- force of friction of marble
with an external ring;
- ball friction force to the
outer ring,
- the power of the ball friction with the inner ring,
- twisting moment of marble,
- the force of gravity of the
ball;
- gravity of the outer ring.
You will take account of the moment of inertia of the rotor drive motor innings 
with
torsional torque 
and
angle of rotation of the rotor 
.
Next, we need to make the differential equations and link them with
thermal processes. The next step is to use “Simulink” programs. graphics will
be built using this program. And also be able to see the change in heat value
in the balls and rings when changing the shaft speed, since it is probably the
most important elements in the bearing.
Literature:
1. http://snr.com.ru/e/about_bearings/about_bearing.htm