Технические науки / 6.Электротехника и радиоэлектроника.

В.А. Медников, С.В. Перелыгин

Санкт-Петербургский государственный институт кино и телевидения

О стабилизации скорости синхронного электродвигателя

Введение

Известно [1], что ротор синхронного двигателя, вращаясь синхронно с полем статора, отстаёт от него по фазе на угол φ (внутренний угол синхронной машины). В установившемся режиме, при постоянной номинальной нагрузке и строго стабильной частоте питающего напряжения угол φ будет поддерживаться постоянным. Однако это не позволяет устранить колебания мгновенной частоты вращения ротора из-за ряда возмущений, которые могут быть вызваны трением в подшипниках качения, дисбалансом вращающихся масс, изменением величины питающего напряжения. Такие колебания выражаются отклонением угла φ относительно его среднего значения и происходят на частоте, отличающейся на порядок в меньшую сторону от частоты вращения самого ротора двигателя [2].

В устройствах кино- и видеоаппаратуры, где предельно важна точность мгновенного углового положения ротора (лазерные записывающие и сканирующие устройства), при высокой скорости вращения допустимое отклонение угла φ от среднего значения не должно превышать нескольких угловых минут [2, 3]. Для хорошо отбалансированного электродвигателя без системы стабилизации амплитуда качаний ротора составила по эксперименту при собственной частоте качаний f_к = 2,3 Гц и коэффициенте демпфирования
ξ₀ = 0,05 <<1 [3].

Расчетные соотношения

Характер качаний определим из следующих соображений. Известно, что динамические свойства синхронного двигателя с достаточной точностью характеризуются передаточной функцией колебательного звена второго порядка [2-4]:

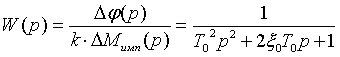(1)
где – изображение по Лапласу колебания фазы,

– изображение кратковременного импульса момента сопротивления,

Т0 – электромеханическая постоянная времени двигателя,

ξ0 – относительный коэффициент демпфирования,

р – оператор Лапласа,

k – коэффициент передачи по возмущению.

При подстановке в выражение (1) и последующем взятии от него модуля можно получить амплитудно-частотную характеристику (АЧХ) двигателя. Остановимся на ней подробнее. На рис. 1 представлена нормированная относительно своего значения на низких частотах АЧХ электродвигателя без использования системы стабилизации при экспериментальных значениях Т₀ и ξ₀.

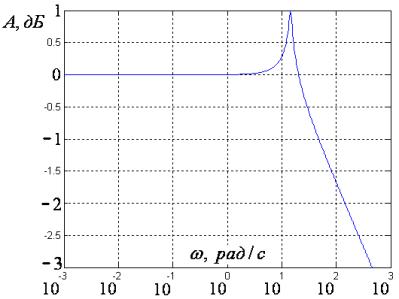
Рис. 1 Исходная АЧХ электродвигателя без использования системы стабилизации.

Для получения малых качаний фазы необходимо стремиться к тому, чтобы АЧХ имела по возможности малые значения и чтобы максимум, соответствующий резонансной частоте, был сдвинут в область низких частот. Для более ясного представления о качаниях фазы ротора двигателя следует перейти во временную область. Для этого решаем дифференциальное уравнение второго порядка и получаем аналитическое выражение изменения фазы во времени [3, 5]:

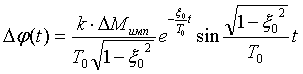(2)
Как следует из (2), параметры колебательного звена влияют на амплитуду качания, его частоту и скорость затухания.

Способ уменьшения качаний фазы ротора до допустимого значения состоит в применении системы автоматической стабилизации частоты вращения ротора двигателя. Данная система сравнивает фазы ротора и статора с учётом угла φ, формирует сигнал ошибки, а также находит его первую и вторую производную и производит суммирование полученных сигналов для последующего воздействия на фазу питающего напряжения. Такой подход учитывает инерционность вращающегося механизма и направлен на то, чтобы скомпенсировать результат влияния возмущающего импульса. Иначе говоря, взятие производных от сигнала ошибки позволяет системе стабилизации не только получить сведения о мгновенном рассогласовании фаз ротора и статора, но и о его дальнейшем изменении, которое требуется предотвратить.

При введении в систему стабилизации пропорционально усиленного сигнала ошибки, а также его первой и второй производных передаточная функция примет вид [4-5]:

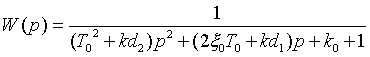(3)

где , , – коэффициенты передачи сигнала ошибки, его первой и второй производной, соответственно.

Приводя выражение (3) к стандартной форме записи передаточной функции колебательного звена второго порядка, имеем:

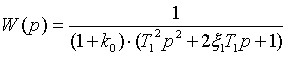(4)
Итак, изменение структуры системы регулирования привело к изменению параметров колебательного звена:

- новая электромеханическая постоянная времени

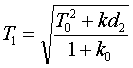(5)
- новый коэффициент демпфирования

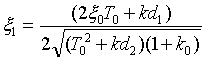(6)
Решая дифференциальное уравнение второго порядка, получаем аналитическое выражение изменения фазы во времени для случая использования системы регулирования [3, 5]:

,

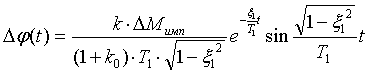где новые параметры колебательного звена и рассчитываются по (5) и (6).

Таким образом, введение коэффициентов передачи сигнала ошибки позволяет изменить частоту и амплитуду качаний фазы ротора и скорость их затухания.

Рассмотрим подробно влияние коэффициентов передачи сигнала ошибки на семейство АЧХ двигателя, построенных в среде Matlab при экспериментальных значениях Т₀ и ξ₀. На рис. 2 приведены АЧХ двигателя для значений kd₁ = 0; 0,01; 0,05; 0,1; 0,2.

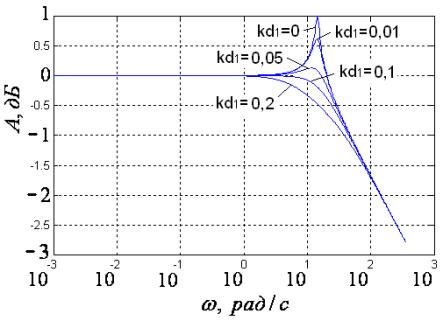
Рис. 2 Семейство АЧХ электродвигателя для разных значений .

На графиках хорошо заметно уменьшение выброса и его сдвиг влево с ростом коэффициента передачи первой производной сигнала ошибки. Последнее (наибольшее) значение соответствует случаю апериодического процесса, когда полностью сглаживается максимум АЧХ.

На рис. 3 приведены АЧХ двигателя для значений k₀ = 0; 1; 5; 10; 50 при фиксированном kd₁ = 0,1.

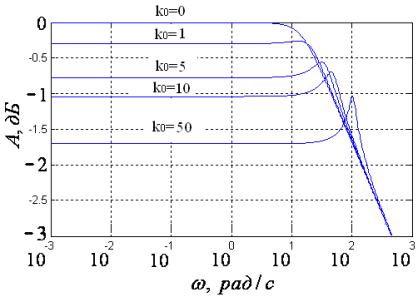
Рис. 3 Семейство АЧХ электродвигателя для разных значений .

Из рисунка следует, что с ростом k₀ наряду с уменьшением площади АЧХ появляется заметный максимум, который смещается в область высоких частот. Тем не менее, при обеспечении требуемого коэффициента уменьшения амплитуды (примерно 40 раз) повышение частоты резонанса не представляется опасным [3].

Для обеспечения более устойчивой стабильности частоты вращения ротора двигателя в систему стабилизации введена вторая производная сигнала ошибки kd₂. На рис. 4 приведены АЧХ двигателя для значений
kd₂ = 0; 0,1; 0,5; 1; 2 при фиксированных kd₁ = 0,1 и k₀ = 50.

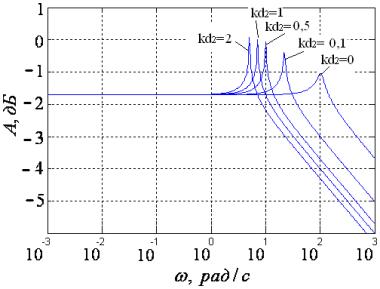
Рис. 4 Семейство АЧХ электродвигателя для разных значений .

Из графиков следует, что с ростом максимум АЧХ смещается в область низких частот, при этом увеличивая своё значение.

Зависимость параметров колебательного звена от коэффициентов передачи сигнала ошибки дает возможность влиять на величину качаний ротора электродвигателя. Задавшись тремя параметрами – во сколько раз требуется уменьшить амплитуду качаний по сравнению с исходной, какими нужно получить частоту качаний и скорость их затухания, – можно найти оптимальное соотношение между коэффициентами передачи сигнала ошибки и его двух производных. При этом соотношении качания ротора электродвигателя теоретически не превысят допустимых значений.

Заключение

Для стабилизации углового положения ротора электродвигателя необходимо использовать систему фазового регулирования. Введение в систему регулирования сигнала ошибки и его производных (первой и второй) позволяет не только ослабить амплитуду качаний фазы ротора, но и также уменьшить частоту качаний. Введение второй производной в закон регулирования описано впервые. В последующих публикациях планируется рассмотреть вопрос разработки и установления оптимальных параметров корректирующего четырехполюсника, выполняющего обработку сигнала ошибки, в том числе, взятие от него двух производных.

Литература

1. Брускин А.Э., Зорохович А.Е., Хвостов В.С. Электрические машины и микромашины. – М.: Высшая школа, 1990. – 432 с.

2. Дроханов А.Н., Иосифов В.Е., Смусь В.С. Стабилизация оптико-механической строчной развёртки с зеркальным барабаном. – Техника кино и телевидения. – 1975. – №6. – С. 41-46.

3. Медников В.А. Система стабилизации строчной развертки для лазерного записывающего устройства. // Тенденции развития отечественной кинотехники: сборник научных трудов. – Л.: ЛИКИ, 1985. – С. 48-56.

4. Танский Е.А. Прецизионные системы стабилизации скорости двигателей. – Л.: Энергия, 1975. – 88 с.

5. Бессекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука, 1975. – 768 с.