Конет І.М., Ленюк М.П.
ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ ПО СОБСТВЕННЫМ
ЭЛЕМЕНТАМ ГИБРИДНОГО ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА БЕССЕЛЯ-ЭЙЛЕРА-ФУРЬЕ НА
ПОЛЯРНОЙ ОСИ
Построим ограниченное на множестве ![]() ={r : r Î(0, R1)
={r : r Î(0, R1)![]() (R1, R2)
(R1, R2)![]() (R2, ¥)} решение сепаратной системы обыкновенных
дифференциальных уравнений Бесселя, Эйлера и Фурье для модифицированных функций
(R2, ¥)} решение сепаратной системы обыкновенных
дифференциальных уравнений Бесселя, Эйлера и Фурье для модифицированных функций
![]() , r Î (0, R1)
, r Î (0, R1)
![]() , r Î (R1,
R2), (1)
, r Î (R1,
R2), (1)
![]() , r Î (R2,
¥)
, r Î (R2,
¥)
по условиям сопряжения
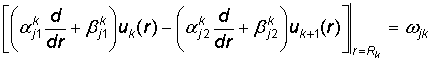 , j, k = 1, 2. (2)
, j, k = 1, 2. (2)
В
системе (1) принимают участие дифференциальный оператор Бесселя [1] 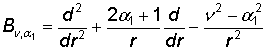 и дифференциальный
оператор Эйлера [2]
и дифференциальный
оператор Эйлера [2] 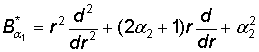 , 2aj +1 > 0.
, 2aj +1 > 0.
Предположим,
что выполнены условия на коэффициенты: qj > 0, ![]() ³ 0,
³ 0, ![]() ³ 0, c1kc2k >
0,
³ 0, c1kc2k >
0, ![]() .
.
Фундаментальную
систему решений для дифференциального уравнения Бесселя (Bn, a – q2)v
= 0 образуют модифицированные функции Бесселя первого рода In, a(qr) и
второго рода Kn, a(qr) [2];
фундаментальную систему решений для дифференциального уравнения Эйлера (![]() – q2)v = 0 образуют функции v1
= r –a – q и v2 = r –a +q [2]; фундаментальную систему решения для
дифференциального уравнения Фурье (d2 / dr2 – q2)v = 0 образуют функции v1 = exp(qr) и v2 exp(–qr) [2].
– q2)v = 0 образуют функции v1
= r –a – q и v2 = r –a +q [2]; фундаментальную систему решения для
дифференциального уравнения Фурье (d2 / dr2 – q2)v = 0 образуют функции v1 = exp(qr) и v2 exp(–qr) [2].
Наличие
фундаментальной системы решений позволяет построить общее решение краевой
задачи (1), (2) методом функций Коши [2, 3]:
u1(r) = A1![]() +
+ 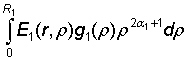 ,
,
u2(r) = A2![]() + B2
+ B2![]() +
+ 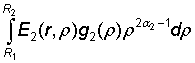 , (3)
, (3)
u3(r) = B3![]() +
+ 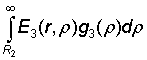 .
.
Здесь
Ej(r, r) – функции Коши [1, 3]:
![]() ,
,
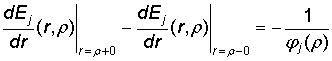 , (4)
, (4)
j1(r) = ![]() , j2(r) =
, j2(r) = ![]() , j3(r) = 1.
, j3(r) = 1.
Введем
в рассмотрение функции:
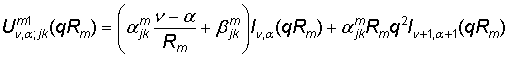 ,
,
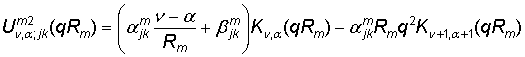 ,
,
![]() .
.
Непосредственно
проверяется, что функция Коши
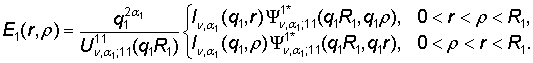 (5)
(5)
Определим функции:
![]() ,
,
![]() ,
,
![]() , j, k = 1, 2,
, j, k = 1, 2,
![]() .
.
Непосредственно
проверяется, что функция Коши
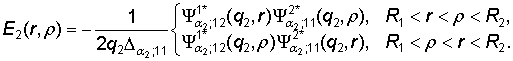 (6)
(6)
Предположим,
что функция Коши
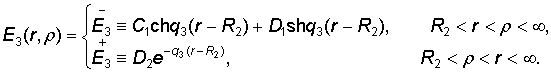
Свойства
(4) функции Коши дают алгебраическую систему:
![]() ,
,
![]() .
.
Отсюда
получаем соотношения:
![]() ,
, ![]() . (7)
. (7)
Дополним
систему (7) алгебраическим уравнением:
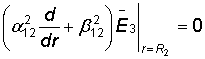 :
: ![]() . (8)
. (8)
Из
алгебраической системы (7), (8) находим, что
D2 = 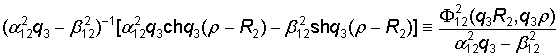 .
.
Этим
функция Коши E3(r, r) определена и в силу симметрии относительно диагонали
r = r имеет структуру:
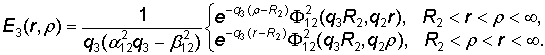 (9)
(9)
Обратимся
к формулам (3). Условия сопряжения (2) дают для определения величин A1,
A2, B2, B3 неоднородную алгебраическую систему из четырех
уравнений:
![]() ,
,
![]() , (10)
, (10)
![]() ,
,
![]() .
.
В алгебраической системе (10) принимают участие функции
G12=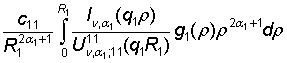 +
+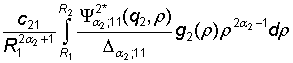 ,
,
G23 = 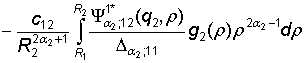 –
– 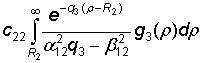 .
.
Введем
в рассмотрение функции:
An, (a); j = ![]() , (a) = (a1, a2),
, (a) = (a1, a2),
![]() =
= ![]() , j = 1, 2,
, j = 1, 2,
![]() =
= ![]() ,
,
![]() =
= ![]() .
.
Предположим,
что выполнено условие однозначной разрешимости краевой задачи (1), (2): для
любого ненулевого вектора ![]() = {q1; q2; q3}
определитель алгебраической системы (10) [4]
= {q1; q2; q3}
определитель алгебраической системы (10) [4]
![]() º
º
º ![]() ¹ 0. (11)
¹ 0. (11)
Определим
главные решения краевой задачи (1), (2):
1) порожденные неоднородностью условий сопряжения
функции Грина
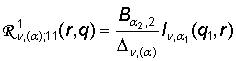 ,
, 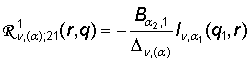 , q = (q1, q2,
q3),
, q = (q1, q2,
q3),
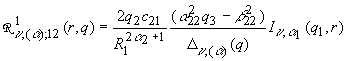 ,
,
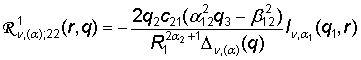 , (12)
, (12)
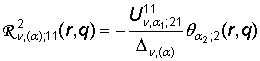 ,
, 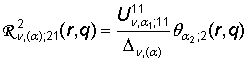 ,
,
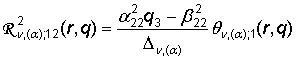 ,
, 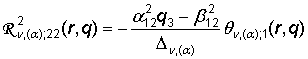 ;
;
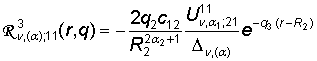 ,
, 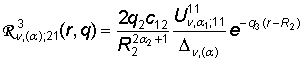 ,
,
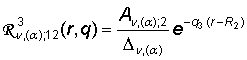 ,
, 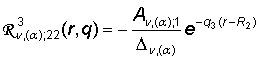 ;
;
2) порожденные неоднородностью системы (1) функции влияния
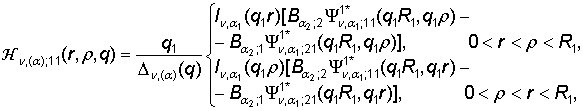
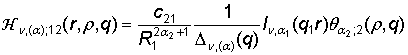 ,
,
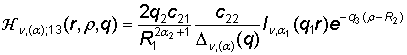 ,
,
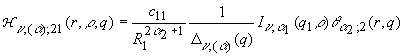 ,
,
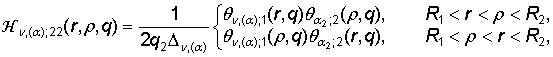 (13)
(13)
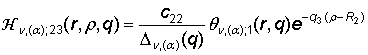 ,
,
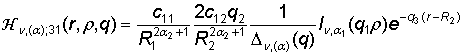 ,
,
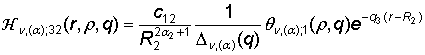 ,
,
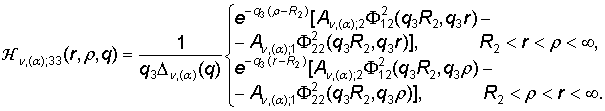
В
результате однозначной разрешимости алгебраической системы (10) в силу условия
(11) и подстановки полученных значений A1,
A2, B2, B3 в формулы (3) имеем единственное решение краевой
задачи (1), (2):
uj(r) = 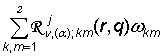 +
+ 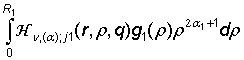 +
+
+ 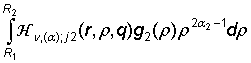 +
+ 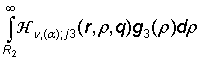 , j =
, j = ![]() . (14)
. (14)
Построим
теперь общее
решение краевой задачи (1), (2) методом
гибридного интегрального преобразования (ГИП), порожденного на множестве ![]() гибридным
дифференциальным оператором (ГДО)
гибридным
дифференциальным оператором (ГДО)
Mn, (a) = q(r)q(R1 – r)
![]() + q(r – R1)q(R2 – r)
+ q(r – R1)q(R2 – r)![]() + q(r – R2) d2 / dr2, (15)
+ q(r – R2) d2 / dr2, (15)
где q(x) – единичная функция Хевисайда [3].
Так как
ГДО Mn, (a)
самосопряженный и имеет одну особую точку r = ¥, то его спектр действительный и непрерывный [5].
Можно считать, что спектральный параметр b Î (0, ¥). Отвечающую ему спектральную вектор-функцию
Vn, (a)(r, b) = q(r)q(R1 – r) Vn, (a); 1 (r, b) + q(r – R1)q(R2 – r)Vn, (a); 2(r, b) +
+
q(r – R2)Vn, (a); 3(r, b)
найдем как ненулевое ограниченное на множестве ![]() решение сепаратной
системы обыкновенных дифференциальных уравнений Бесселя, Эйлера и Фурье
решение сепаратной
системы обыкновенных дифференциальных уравнений Бесселя, Эйлера и Фурье
![]() , r Î (0, R1)
, r Î (0, R1)
![]() , r Î (R1, R2), (16)
, r Î (R1, R2), (16) ![]() , r Î (R2,
¥)
, r Î (R2,
¥)
по условиям сопряжения
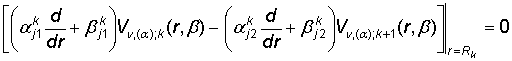 , j, k = 1, 2. (17)
, j, k = 1, 2. (17)
Здесь bj = (![]() )1/2,
)1/2, ![]() ³ 0, j =
³ 0, j = ![]() .
.
Фундаментальную
систему решений для дифференциального уравнения Бесселя (![]() +
+ ![]() )v = 0 образуют функции v1 =
)v = 0 образуют функции v1 = ![]() и v2 =
и v2 = ![]() [1]; фундаментальную
систему решений для дифференциального уравнения Эйлера (
[1]; фундаментальную
систему решений для дифференциального уравнения Эйлера (![]() +
+ ![]() )v = 0 образуют функции [2] v1 =
)v = 0 образуют функции [2] v1 = ![]() cos(b2lnr) и v2 =
cos(b2lnr) и v2 = ![]() sin(b2lnr) [2]; фундаментальную систему решений для
дифференциального уравнения Фурье (d2 / dr2 +
sin(b2lnr) [2]; фундаментальную систему решений для
дифференциального уравнения Фурье (d2 / dr2 + ![]() )v = 0 образуют функции v1 = cos b3r и v2 = sin b3r [2].
)v = 0 образуют функции v1 = cos b3r и v2 = sin b3r [2].
Если
положить
Vn, (a); 1(r, b) = A1![]() ,
,
Vn, (a); 2(r, b) = A2![]() cos(b2lnr) + B2
cos(b2lnr) + B2![]() sin(b2lnr), (18)
sin(b2lnr), (18)
Vn, (a); 3(r, b) = A3cos(b3r) + B3sin(b3r),
то условия сопряжения (17) дают для определения величин Aj (j = ![]() ) и Bk (k = 2, 3) алгебраическую систему из четырех уравнений:
) и Bk (k = 2, 3) алгебраическую систему из четырех уравнений:
![]() = 0, j = 1, 2,
= 0, j = 1, 2,
![]() . (19)
. (19)
В
этой алгебраической системе принимают участие функции
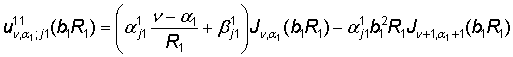 ,
,
![]() =
= ![]() –
– ![]() ,
,
![]() =
= ![]() +
+ ![]() ,
,
![]() ,
,
![]() .
.
Алгебраическая
система (19) всегда совместная, т.е. имеет ненулевое решение, получаемое
стандартным приемом [4]. В результате подстановки полученных значений Aj
и Bk в равенства (18) имеем:
Vn, (a); 1(r, b) = c21b2![]() c22b3
c22b3![]() ,
,
Vn, (a); 2(r, b) = c22b3[![]() ],
],
Vn, (a); 3(r, b) = wn, (a); 2(r, b)cos b3r – wn, (a); 1(r, b)sin b3r. (20)
В
равенствах (20) приняты обозначения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() , j = 1, 2.
, j = 1, 2.
Введем
в рассмотрение весовую функцию
s (r) =q(r)q(R1 – r)s1![]() + q(r – R1)q(R2 – r) s2
+ q(r – R1)q(R2 – r) s2 ![]() + q(r – R2) s3,
+ q(r – R2) s3,
где ![]() ,
, ![]() , s3 = 1,
, s3 = 1,
и спектральную плотность
Wn, (a)(b) = b[b3(b)]–1([wn, (a); 1(b)]2 + [wn, (a); 2(b)]2)–1.
Наличие
спектральной функции Vn, (a)(r, b), весовой функции s(r) и
спектральной плотности Wn, (a)(b) позволяет ввести ГИП (прямое Hn, (a) и
обратное ![]() ), порожденное на множестве
), порожденное на множестве ![]() ГДО Mn, (a) [5]:
ГДО Mn, (a) [5]:
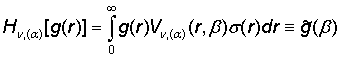 , (21)
, (21)
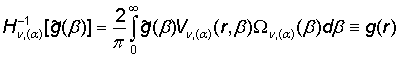 . (22)
. (22)
Здесь
вектор-функция g(r) = {g1(r); g2(r); g3(r)} – любая
функция из области определения ГДО Mn, (a).
В
основе применения ГИП, введенного правилами (21), (22), для решения
соответствующих задач лежит основное тождество интегрального преобразования ГДО
Mn, (a): если
вектор-функция f(r) = {![]() [g1(r)];
[g1(r)]; ![]() [g2(r)];
[g2(r)]; ![]() } непрерывная на множестве
} непрерывная на множестве ![]() , а функции gj(r) удовлетворяют условиям сопряжения (2) и условиям
ограниченности
, а функции gj(r) удовлетворяют условиям сопряжения (2) и условиям
ограниченности
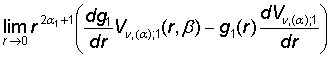 = 0,
= 0,
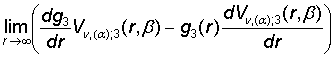 = 0,
= 0,
то имеет место равенство
Hn, (a)[Mn, (a)[g(r)]]=![]()
В
равенстве (23) приняты обозначения:
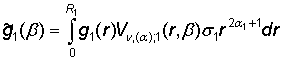 ,
, 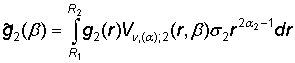 ,
,
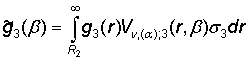 ,
, 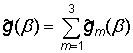 , hm
=
, hm
= ![]() ,
,
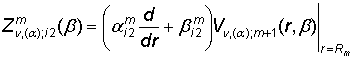 , i, m = 1, 2.
, i, m = 1, 2.
Единственное
решение краевой задачи (1), (2), построенное по известной логической схеме
методом ГИП, введенного по правилам (21), (22) [5], имеет
структуру:
uj(r) = 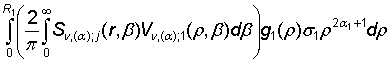 +
+
+
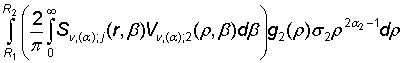 +
+
+
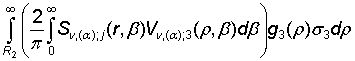 + (24)
+ (24)
+ 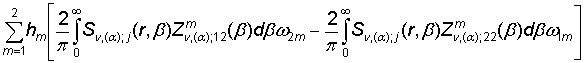 ,
,
j = ![]() .
.
Здесь
принимает участие функция
![]() , q2 = max{
, q2 = max{![]() ;
; ![]() ;
; ![]() }.
}.
Сравнивая
решения (14) и (24) в силу единственности, получаем такие формулы вычисления полипараметрических
несобственных интегралов:
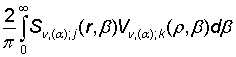 =
= 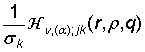 , j, k =
, j, k = ![]() , (25)
, (25)
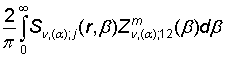 =
= ![]() ,
m = 1, 2, j =
,
m = 1, 2, j = ![]() , (26)
, (26)
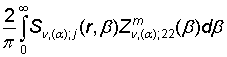 =
= ![]() , m = 1, 2, j =
, m = 1, 2, j =
![]() . (27)
. (27)
Функции
![]() определены по
формулам (13), а функции Грина
определены по
формулам (13), а функции Грина ![]() – по формулам (12).
– по формулам (12).
Поскольку
правые части в формулах (25) – (27) не зависят от неравенства (![]() ) ³ 0, то можно положить
) ³ 0, то можно положить ![]() , суживая при этом семью несобственных интегралов.
, суживая при этом семью несобственных интегралов.
Результатом
проведенных исследований есть утверждение.
Основная теорема. Если вектор-функция g(r) удовлетворяет
условиям положения об основном тождестве и выполняется условие (11)
однозначной разрешимости краевой задачи (1), (2), то справедливы формулы (25) –
(27) вычисления несобственных полипараметрических интегралов по собственным
элементам ГДО Mn, (a), определенного равенством (14).
Отметим,
что результаты работы (формулы (25) – (27))
пополняют справочную математическую литературу.
ЛИТЕРАТУРА
1.
Ленюк М.П. Исследование
основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев,
1982. – 62 с. – (Препринт / АН УССР. Ин-т математики; 83.3).
2.
Степанов В.В. Курс
дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.
3.
Шилов Г.Е. Математический анализ.
Второй специальный курс. – М.: Наука, 1965. – 328 с.
4.
Курош А.Г. Курс высшей
алгебры. – М.: Наука, 1971. – 432 с.
5.
Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є,
Бесселя, Лежандра). Частина 1. – Тернопіль: Економ. думка, 2004. – 368 с.