Математика / 4.Прикладная математика

Таджигитов А.А., Климов Е.В., Дуткин М.А.

Северо-Казахстанский государственный университет им. М.Козыбаева, Республика Казахстан, г. Петропавловск

О МАКСИМАЛЬНЫХ ФУНКЦИЯХ В ПРОСТРАНСТВАХ Lp

Понятие максимальной функции и максимального неравенства возникли в 30-40 г.г. ХХ века. С того времени максимальные неравенства постоянно исследовались и дополнялись новыми сведениями. С помощью максимальных функций можно решить некоторые задачи математического анализа, функционального анализа, математической физики. С этим понятием связаны имена многих известных ученых: Харди Ж. Г., Литтлвуд Ж.Е., Стейн И. и др.

По определению максимальная функция задается следующим равенством:

,

здесь – шар радиуса с центром в точке и – его мера. Иногда такую функцию называют максимальной функцией Харди-Литллвуда. Функция может быть неограниченной для любого . Рассмотрим основную теорему о максимальной функции. Эта теорема для впервые доказана Харди и Литтлвудом, а -мерный вариант – Винером.

Теорема 1. Пусть функция определена на .

а) если , где , то функция почти всюду конечна;

б) если , то для любого : , где – константа, зависящая только от размерности (например, можно положить );

в) если , где , то и , где зависит только от и размерности .

Следствие. Если , , или, в более общем случае, если локально суммируема, то для почти всех .

Теорема 1 доказывается при помощи леммы Витали или леммы о покрытиях [1, 35 стр.].

Рассмотрим максимальную функцию как максимальный оператор и докажем ограниченность этого оператора. Оператор рассмотрим в следующем виде: .

Здесь имеет место следующая теорема:

Теорема 2. Оператор для будет ограниченным.

Доказательство. Действительно, если и , тогда и .

Из этого неравенства следует ограниченность оператора в пространстве .

До этого момента рассматривалось пространство для . А какими свойствами обладает максимальная функция для ?

В этой связи справедлива следующая теорема:

Теорема 3. Пусть , где , тогда и не выполняется неравенство .

Доказательство. Определим функцию в следующем виде: , если и в противном случае.

и , где . Если , тогда .

Это утверждение доказывается при помощи теоремы вложения для пространства . Действительно, если и , то и , тогда , но .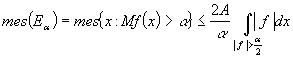

При неравенство не выполняется. Теорема 3 доказана.

Пример. Пусть . В качестве шара с центром в точке радиуса рассмотрим отрезок на прямой .

Зададим функцию следующим образом: , где – некоторая постоянная величина. Тогда .

Решение. Найдем максимальную функцию функции по формуле .

Так как , то . Тогда ,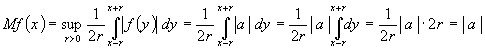

.

Литература:

1. Стейн И.М. Сингулярные интегралы и дифференциальные свойства функций. – М.: «Наука», 1973. – 342 с.

2. Буренков В.И. Функциональные пространства. Пространства Lp.
– М.: «Наука», 1987. – 92 с.