Лебедев Е.П., Гурвич Ю.А.
Белорусский национальный технический университет, г. Минск
РАСЧЁТ
ПАРАМЕТРОВ РУЛЕВЫХ ТРАПЕЦИЙ
В связи с наличием в
литературе пяти различных гипотез выбора геометрии рулевых трапеций, каждая из
которых справедлива только для какого-то одного из режимов движения машины,
поставим задачу: разработать универсальную методику автоматизации
проектирования рулевых трапеций различных типов.
Предположим, что
движение пневмоколесной машины по криволинейной траектории без бокового
скольжения колес (или с минимальным боковым скольжением колес) описывается
уравнением
bN=fN (a,l¢1N,…,l¢mN), (1)
где l¢1,…,l¢m - различные параметры машины (геометрические,
инерционные и т. д.);
m - количество параметров;
bN – угол поворота внешнего управляемого колеса машины.
Уравнение (1) при (N=1,4) отображает каждую из четырех гипотез выбора
геометрии рулевой трапеции (Чудакова, Фиалы, Гауха и Ширера, Хасельгрубера), а
при N=5 это уравнение представляет собой уравнение
котангенсов.
ctgβ
- ctgα = L / M. (2)
В общем виде уравнение
рулевой трапеции имеет вид
bT= Ф(a, l1,…,lj,g1,…,gm), (3)
где bT – угол поворота внешнего управляемого колеса
машины (рисунок 1), m=j+m.
Чтобы движение машины с рулевой трапецией наилучшим образом (но тем не менее
приближенно) отобразило зависимость (1), необходимо варьировать все значения
управляемых параметров l1, lj. Затем из набора совокупностей значений параметров
выбирается такая совокупность параметров (l1, lj; g1, gm), которая соответствует максимальному приближению
(близости) зависимости (3) к зависимости (1) или (2).
При этом
возникают вопросы, что принять за меру близости двух зависимостей и как
выразить математическую степень близости зависимостей bт и bN друг к другу.
Известно, что в
пространстве функций х(t), определенных
и непрерывных при а £ t £ b существуют
различные нормы: чебышевская с равномерной сходимостью по ней и гильбертовская
со среднеквадратичной сходимостью.
251658240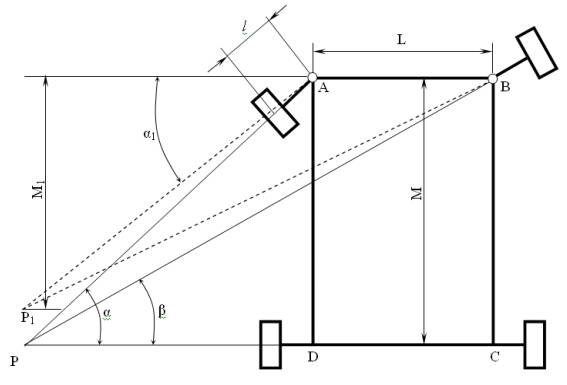
Рисунок 1- Поворот машины без
учета боковой эластичности шин, центр
масс которой совершает криволинейное движение.
Точка Р соответствует
идеальному повороту машины, а точка Р1 повороту машины,
осуществленному с помощью какой-либо рулевой трапеции. Примем за меры близости двух зависимостей bТ и bN чебышевскую и гильбертову нормы. Тогда в
качестве наилучшего приближения зависимости (3) к (1) предлагаются критерии F1N и
F2N.
Предварительно введем число точек ( i ) на
кривых, отображающих зависимости bТ и bN.
Тем самым непрерывный
процесс аппроксимируем дискретным. Критерии F1N и
F2N в
этом случае имеют вид
1£ i £N1![]()
![]()
F1N = max bNi - bТi , I=1,N1 , (4)
![]() . (5)
. (5)
Литература
1. Андреев А.Ф. Исследование движения колесной машины с большими углами поворота управляемых колес// Конструирование и эксплуатация автомобилей и тракторов. Мн., 1991. Вып.6, с. 60-66.
2. Гурвич Ю.А. Практические, научные и методические предпосылки введения многокритериального синтеза и других прогрессивных технологий обучения в статику, кинематику и динамику. Теоретическая и прикладная механика: сб. науч. трудов. Мн.: УП «Технопринт», 2003.-252с.
3. Гурвич Ю.А. Новые прикладные критерии колебательной и апериодической устойчивости движения колес транспортных средств. Актуальные проблемы в динамике и прочности в теоретической и прикладной механике: Сб. науч. тр. – Мн.: 2001. с.148-162.
4. Исследование автоколебаний и стабилизации управляемых колес рулевого привода автобусов и автомобилей. Руководитель Ю. А. Гурвич.- № ГР 20012549,20012550/07.07.2001 Бел ICA ; инв. № ГНТП И-5808729.95-2002 ГП МАЗ.