Екологія / 6. Екологічний моніторинг

К. т. н. Холковський Ю. Р., студ. Березівський М. Ю.

Національний авіаційний університет України, Державний заклад "Київський коледж зв’язку"

ДЕЯКІ АСПЕКТИ МОДЕЛЮВАННЯ БАГАТОПАРАМЕТРИЧНИХ ЕКОЛОГІЧНИХ ОБ’ЄКТІВ, ПРОЦЕСІВ ТА ЯВИЩ

Комп’ютерне моделювання різноманітних просторових об’єктів у сучасних технологічних процесах та компонентах навколишнього середовища набуває надзвичайно швидкого розвитку. Зокрема, це стосується моніторингу та прогнозування забруднень великих території, водних об’єктів, моделювання розсіювання хмар в атмосфері, розповсюдження пожеж тощо. Також необхідно підкреслити роль саме дискретного геометричного моделювання таких об’єктів та середовищ, що дозволяє розробити дискретні математичні моделі, які поєднують в собі різноякісні параметри, поєднання яких у континуальній моделі просто неможливе.

З математичної точки зору такі екологічні процеси й явища відносять до динамічних, тобто параметри яких безперервно змінюються у часі й просторі.
У таких випадках виникає нагальна потреба в розробці нових методів і підходів щодо моделювання багатопараметричних геометричних об’єктів і процесів.
Як виявилось у дослідженні, метод інтерполяції дискретних масивів, як спосіб геометричного моделювання багатопараметричних об’єктів та явищ, є найбільш придатним щодо опису поведінки різноманітних екологічних систем і процесів.

Дискретні моделі, як правило, застосовують для моделювання складних об’єктів, які не піддаються аналітичному опису. Саме такі моделі оптимально підходять для подальшого проектування екосистем та прогнозування розповсюдження різноманітних забруднень, що пов’язано зі значним ускладненням формоутворюючих факторів при проектуванні таких систем та багатопараметричних процесів і явищ. Для цього можуть бути використані різні дискретно-інтерполяційні схеми, що надають змогу отримати однопараметричну множину певних багатопараметричних об’єктів, процесів чи явищ.

Для більш точного відтворення різноманітних природних та техногенних процесів і явищ доцільним виявляється передбачити ускладнення дискретних математичних моделей шляхом підвищення вимірності дискретної інтерполяційної схеми. Наприклад, можна запропонувати застосування двовимірних та навіть n-вимірних схем. Вважаємо, що у цьому контексті оптимальним є вибір інтерполяційних поліномів Лагранжа, що обумовлено відносною простотою у використанні таких поліномів, необов’язковою рівномірністю розташуванням вузлів інтерполяції, а також можливістю представлення різної кількості вузлів інтерполяції по кожній із змінних.

Нетрадиційність запропонованого підходу полягає в тому, що під вузлами інтерполяції ми розуміємо не точки, а складніші об’єкти − наприклад, лінії та поверхні, або певні процеси (екологічні, хімічні, фізико-хімічні тощо) чи явища, представлені у вигляді деяких функціоналів як сукупності їх властивостей і параметрів. Отже, під схемою інтерполяції у подальшому розуміємо схему розташування саме таких її вузлів.

Однопараметричні або n-параметричні множини різної природи, що можуть бути отримані таким шляхом, є дискретними математичними моделями багатопараметричних об’єктів і процесів, у тому числі й екологічних.
І елементом таких множин є деяка дискретна функція, або функціонал, який у загальному випадку може бути представлений як дискретний чисельний масив, розмірність якого змінюється в певних межах.

Функції, що однозначно не можуть бути спроекційовані на жодну з координатних осей чи площин, задаються неявно або параметрично. Тоді їх інтерполювання зводиться до розміщення у вузлах інтерполяції певних базових функцій – дискретних масивів. Це, в свою чергу, надає змогу отримати деякий функціонал Ф(p_i,j), з вектором параметрів, що включає в себе інтерполяційний параметр, координатні змінні, параметри, що характеризують форму й положення об’єктів, а також фізико-хімічні або екологічні характеристики природних та технологічних процесів і явищ:

Ф(p₁, p₂, p₃, … , p_i, … , p_j , …) = M[i, j].

Наприклад, у випадку тривимірної інтерполяції, що, як правило, застосовується для складних і багатокомпонентних систем, через вузлові точки проходить деяка гіперповерхня, що являє собою многочлен 3-х змінних,
а формула матиме вигляд:

,

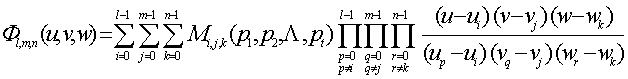де l, m, n − кількість вузлів інтерполяції уздовж кожного її напрямку; u, v, w − інтерполяційні параметри координат; p₁, p₂, …p_t − формоутворюючі, фізико-хімічні та екологічні параметри.

Таким чином, запропонований нами підхід дає змогу включати в однопараметричну множину об’єкти, що мають різну структуру й властивості. Особливо актуальним це виявляється для великої кількості багатопараметричних процесів, параметри яких можуть змінюватися як у просторі, так й у часі.

Вважаємо, що застосування такого підходу до моделювання складних екологічних явищ і систем, що характеризуються великою кількістю різноякісних параметрів, які неможливо функціонально-аналітично поєднати у звичайній математичній моделі, є надзвичайно перспективним. Отримавши формулу інтерполювання дискретних масивів у загальному випадку, маємо можливість моделювати достатньо складні об’єкти, процеси і навіть явища та середовища, що мають певну анізотропність властивостей у просторі та характеризуються великою кількістю параметрів, які можуть мати різноманітну структуру.